Приближенное решение нелинейных алгебраических и трансцендентных уравнений
Тема 5. Приближенное решение нелинейных алгебраических и трансцендентных уравнений.
Нелинейные алгебраические и трансцендентные уравнения в общем виде можно представить как
f(x) = 0,
здесь f(x) - некоторая функция от аргумента x, которую будем предполагать непрерывной и дифференцируемой. Решить такое уравнение - это найти его корни, т.е. такие значения аргумента, при подстановке которых уравнение превращается в равенство. В нелинейных уравнениях корней :
- может не быть вовсе;
- может быть конечное число (например, один, два и т.д.);
- может быть бесчисленное множество.
Рещение таких уравнений аналитическими методами, как правило, невозможно или очень сложно. Поэтому (наиболее часто) нахождение корней таких уравнений производится приближенными методами. Подавляющее большинство таких методов требует предварительного отделения корней. Оно заключается в поиске для каждого корня xi этого уравнения такого интервала (ai, bi), внутри которого он содержится. После такого отделения используют методы приближенного нахождения корней для их уточнения с заданной точностью. Имеются некоторые из методов (в частности, метод Рыбакова), которые не требуют проведения отделения корней.
Рекомендуемые материалы
Отделение корней.
Для выполнения отделения корней уравнения используются аналитические и графические методы.
Суть аналитических методов заключается в анализе знаков исходной функции в точках, равных корням производной исходной функции (или близких к ним), а также знаков предельных значений функции при стремлении аргумента к “плюс” и “минус” бесконечности. Если перемена знака происходит - значит в этом интервале имеется корень исходной функции. При желании - интервал можно сузить, проведя просчет значений функции внутри него с некоторым шагом и анализируя знаки полученных при этом значений.
Если функция f(x) является полиномом степени n, то имеется правило Ньютона для нахождения верхней и нижней границ расположения корней. Правило гласит, что если имеется число q, такое что при всех х > q фукнкция и все ее производные до (n –1) порядка положительны, то число q является верхней границей корней этого полинома. Эсли имеется число h такое, что оно является верхней границей корней полинома f(-x), тогда число -h является нижней границей корней полинома f(x).
Пример 1. Произвести отделение корней уравнения  , где
, где  .
.
Найдем производную заданной функции. Получим  . Найдем корень производной. Получим :
. Найдем корень производной. Получим :
 ,
,  ,
,  .
.
Таким образом, мы установили, что производная заданной функции имеет только один корень.
Найдем теперь знаки заданной функции при х=0.82, и при х→ - ∞ и х → +∞. Получим :
| х | - ∞ | 0.82 | +∞ |
| Знак f(x) | + | - | + |
Из таблицы видно, что функция имеет две перемены знака, следовательно - исходное уравнение имеет два корня, один из которых находится внутри интервала (- ∞, 0.82), другой - внутри интервала (0.82, +∞). Поскольку найденные интервалы являются очень широкими и неудобными для практического использования, попытаемся сделать их более узкими. Для этого в интервале от -3 до +4 с шагом, равным 1 произведем вычисление знаков исходной функции. Получим :
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| Знак f(x) | + | + | + | - | - | + | + | + |
Отсюда видно, что корни уравнения  лежат в интервалах (-1, 0) и (1, 2).
лежат в интервалах (-1, 0) и (1, 2).
Следавательно, отделение корней (аналитическим методом) заданного уравнения произведено.
Суть графических методов заключается в просчете значений исходной функции в некоторых точках и построении ее графика, по нулям которого (т.е. точкам пересечения или касания графика оси ОХ) с учетом погрешностей такого построения определяются интервалы нахождения корней. Если построение графика исходной функции затруднено - можно представить ее как разность двух (более простых) функций f(x) = f1(x) - f2(x). После этого, на одной и той же координатной плоскости необходимо построить графики каждой из этих функций. Затем приближено определить допустимые пределы, в которых находятся абсциссы точек пересечения этих графиков. Они и дадут интервалы, в которых находятся искомые значения корней исходного уравнения. Пример применения графических методов отделения корней показан в примере 2 ниже.
Приближенные методы уточнения корней.
Каждый из таких методов позволяет уточнить значение определенного (отделенного в некотором интервале) корня с заданной точностью, которая задается некоторым достаточно малым числом (обычно это число обозначается символом e). Рассмотрим несколько таких методов.
Метод половинного деления. Поиск приближенного значения корня x, заключенного внутри найденного интервала (a, b), методом половинного деления возможен только тогда, когда значения функции в точках a и b различны по знаку, т.е. должно выполняться условие f(a) · f(b) < 0.. Суть метода заключается в сравнении знаков исходной функции в концах интервала и в его средине - точке x, определяемой по формуле x = (a.+ b)/2. После этого производится перенос в точку x того конца интервала, знак значения функции в котором совпадает со знаком ее в точке x. Таким образом, за один шаг интервал, в котором находится корень уравнения, уменьшается в два раза, причем знаки значений функции на концах нового интервала (a, b) остаются разными.
Так необходимо продолжать до тех пор, пока длина интервала не станет меньшей заданной точности для нахождения значения корня. В этом случае за приближенное значение корня берется средина последного отрезка. Следует отметить, что этим методом возможно нахождение (с заданной точностью) приближенного значения корня, в котором функция меняет свой знак. Если же функция не меняет свой знак (т.е. ее график только касается оси абсцисс и возвращается в ту же полуплоскость относительно оси ОХ - такие корни являются кратными корнями четной степени), то нахождение корня этим методом невозможно.
Вычисления по методу половинного деления удобно производить с использованием таблиц (возможно в Excel) следующего вида
| j | A | f(a) | B | f(b) | Х | f(x) | b – a |
| 0 |
| ||||||
| 1 | |||||||
| … |
Для контроля за правильностью выполнения расчетов необходимо следить за значениями функции f(x) в предпоследнем столбце таблицы. Значения в нем должны постепенно (не обязательно монотонно) уменьшаться по абсолютной величине и в последних итерациях долны быть достаточно близкими к нулю. Если это не так - где-то произошла ошибка, расчеты необходимо перепроверить.
Пример 2. Используя метод половинного деления найти приближенное значение наибольшего корня уравнения y = x2 – 3 – ln(x) с точностью e = 0.005.
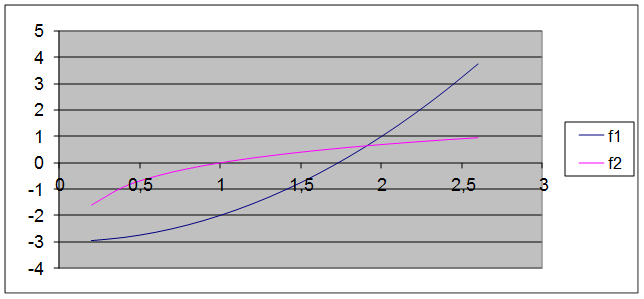 |
Произведем сначала отделение корней. Для этого воспользуемся графическим методом. Разобьем функцию f(x) = x2 – 3 – ln(x) на разность двух более простых функций f(x) = f1(x) – f2(x), где f1(x) = x2 – 3 и f2(x) = ln(x), и построим графики зависимостей y = f1(x) и y = f1(x) на одной координатной плоскости. Получим графики обоих функций
По графику определим границы интервала, внутри которого находится абсцисса точки пересечения графиков, корень исходного уравнения. За левую границу интервала примем значение 1, за правую - 2. Таким образом, мы получили интервал (a, b) = (1, 2), внутри которого содержится искомый нами корень заданного уравнения.
Дальнейшее уточнения значения корня с заданной точностью проведем с использованием таблицы указанного выше вида. После выполнения всех необходимых расчетов (в Excel) она примет следующий вид :
| i | a | f(a) | B | f(b) | Х | f(x) | b-a |
| 0 | 1 | -2 | 2 | 0,3069 | 1,5 | -1,1555 | 1 |
| 1 | 1,5000 | -1,1555 | 2 | 0,3069 | 1,7500 | -0,4971 | 0,5000 |
| 2 | 1,7500 | -0,4971 | 2 | 0,3069 | 1,8750 | -0,1130 | 0,2500 |
| 3 | 1,8750 | -0,1130 | 2 | 0,3069 | 1,9375 | 0,0925 | 0,1250 |
| 4 | 1,8750 | -0,1130 | 1,9375 | 0,0925 | 1,9063 | -0,011 | 0,0625 |
| 5 | 1,9063 | -0,0113 | 1,9375 | 0,0925 | 1,9219 | 0,0403 | 0,0313 |
| 6 | 1,9063 | -0,0113 | 1,9219 | 0,0403 | 1,9141 | 0,0144 | 0,0156 |
| 7 | 1,9063 | -0,0113 | 1,9141 | 0,0144 | 1,9102 | 0,0015 | 0,0078 |
| 8 | 1,9063 | -0,0113 | 1,9102 | 0,0015 | 1,9082 | -0,0049 | 0,0039 |
Так как на последнем (восьмом) шаге величина b – a оказалась меньше заданной точности, т.е. меньше 0.005, то процесс вычислений заканчиваем и за искомое значение корня примем последнее значение величины x, равное 1.908. Для дополнительного контроля правильности проведенных расчетов обратим внимание на значение f(x) при найденном значении x. Оно равно -0.0049, т.е. является достаточно близким к нулю. Это дает основание предполагать, что расчеты проведены правильно.
Метод Ньютона (другое название - метод касательных). Идеи этого метода и их представление в координатной системе (на графике) должны быть знакомы студентам по курсу высшей матаматики. Поиск приближенного значения корня x, заключенного внутри найденного интервала (a, b) методом Ньютона начинается с выбора начального приближения искомого корня x0. В качестве его можно взять значение одного из концов найденного интервала (a, b) либо любую точку из этого интервала. Важно, чтобы выбранное значение начального приближения удовлетворяло системе из двух неравенств :
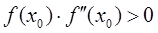
 . (5.1)
. (5.1)
В этом случае будет обеспечено условие сходимости итерационного процесса.
После выбора начального приближения производится уточнение значения корня по следующей итерационной формуле :
 (5.2)
(5.2)
здесь j - номер итерации. Если вычисленное значение производной близко к нулю (случай кратного корня) - вместо него (в знаменателе формулы (5.2)) необходимо использовать любое большее по абсолютной величине число, знак которого совпадает со знаком производной вблизи искомого корня. В частности, можно производить вычисления по формуле
 . (5.3)
. (5.3)
Эта формула пригодна для использования вместо формулы (5.2) независимо от величины производной, однако скорость сходимости итерациооного процесса замедлится.
Процесс итерационного уточнения корней завершается в том случае, если в двух последующих итерациях достигнуты значения, отличающиеся менее чем на величину заданной точности e, т.е. если будет выполнено неравенство  . В этом случае за найденное приближенное значение корня принимают значение величины xj+1.
. В этом случае за найденное приближенное значение корня принимают значение величины xj+1.
Неверный выбор начального приближения может привести к «разбросу» находимых значений приближений и отсутствию их сходимости к значению корня. Чаще всего в таких ситуациях процесс уточнения корня приведет к выходу за пределы интервала (a, b).
Вычисления по этому методу удобно производить с использованием таблиц (возможно в Excel) следующего вида :
| J | X | f (x) | f’(x ) | Dx = ff(x) / f’(x) |
| 0 |
|
|
|
|
| 1 |
|
|
|
|
| … |
|
|
|
|
Для контроля за правильностью выполнения расчетов необходимо (как и в методе половинного деление) следить за значениями функции f(x) в соответствующем столбце таблицы. Значения в нем должны постепенно и монотонно уменьшаться по абсолютной величине и в последних итерациях долны быть достаточно близкими к нулю. Если это не так - где-то произошла ошибка, расчеты необходимо перепроверить.
Пример 3. Используя метод Ньютона найти приближенное значение наибольшего корня уравнения y = x2 – 3 – ln(x) с точностью 0.005.
Вместо поиска начального приближения искомого корня воспользуемся интервалом, внутри которого он заключен, найденным при нахождении его методом половинного деления. Имеем a =1 и b = 2. В качастве начального приближения возьмем тот конец интервала, который удовлетворяет системе неравентсв (5.1). Имеем
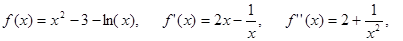
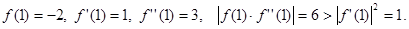
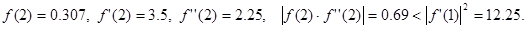
Следовательно, за начальное приближение необходимо взять правый конец интервала, т.е. положить  .
.
Произведем необходимые вычисления и их результаты поместим в таблицу. Получим
| I | X | f(x) | f'(x) | f(x) / f'(x) |
| 0 | 2 | 0,30685 | 3,5 | 0,08767 |
| 1 | 1,91233 | 0,00868 | 3,30173 | 0,00263 |
| 2 | 1,90970 | 0,00000 | 3,295757 | 0,00000 |
Уже на втором шаге получено искомое значение корня (с заданной точносью). Оно совпало со значением, полученным методом половинного деления.
Метод Рыбакова. Этот метод позволяет вычислить приближенные значения всех корней уравнения на заданном интервале (a, b) без проведения их предварительного отделения. Длина интервала (a, b) может быть достаточно большим и в нем может находиться несколько корней исходного уравнения. Для того, чтобы воспользоваться этим методом, необходимо определить значение вечины М, которая должна быть не меньше наибольшего значения абсолютной величины производной исходной функции на всем заданном интервале, т.е.
 . (5.4)
. (5.4)
Суть метода удобно рассмотреть по риcунку 5.1, на котором в координатной плоскости XOY изображен график абсолютной величины исходной функции (на интервале (a, b).
Начиная от левого конца интервала (т.е. положив x0=a), из точки с координатами (х0, f(х0)) под углом, тангенс которого равен значению М, проводят прямую линию до пересечения с осью ОХ. В точке пересечения получим очередную точку x1, значение которой может быть посчитано из предыдущего ее значения по формуле
 . (5.5)
. (5.5)
Дальше из новой точки (x1, f(x1)) проведем аналогичную операцию. Так будем продолжать до тех пор, пока шаг движения вперед станет очень малым (меншим заданной точности). В такой ситуации :
- последнюю точку xj примем за приближенное значение очередного корня
- увеличим величину xj на значение точности e
- продолжим тот же процесс до получения следующего корня или до достижения конечной точки интервала - b.
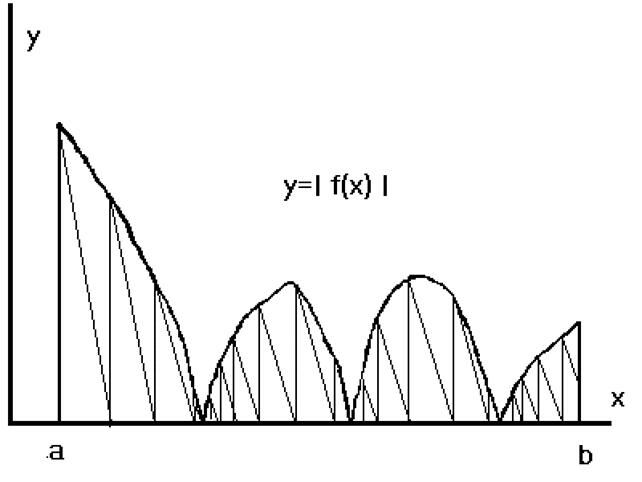
Рис. 5.1. Схема к методу Рыбакова поиска корней функции на интервале.
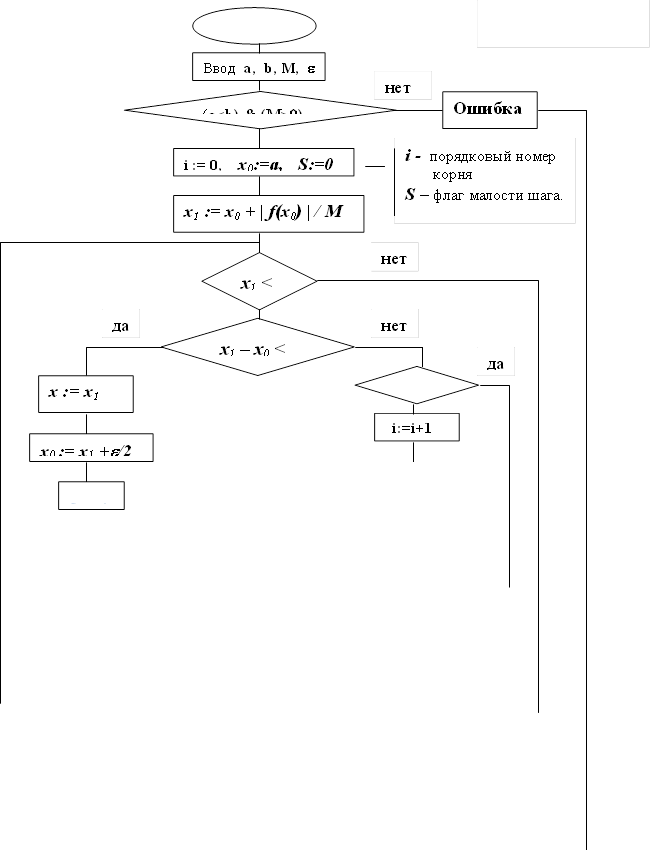
Более четко алгоритм этого метода в виде блок-схемы приведен на рис. 5.2, который студентам необходимо разобрать в деталях.
Обратите внимание на лекцию "Симметрия и асимметрия в композиции".
Выполнение условия (5.4) обеспечивает прохождение каждой прямой (наклонной) линии под кривой, не пересекая ее. Если это условие окажется нарушеным - наклонная линия может пересечь график абсолютной величины функции и какой-то корень уравнения может быть пропущен.
На практике, для проведения поиска корней конкретной функции по методу Рыбакова необходима разработка программы для ПЭВМ на алгоритмическом языке по приведенному выше алгоритму. В этой программе должна быть заложена эта конкретная функция f(x). Но, значение величины М можно не вводить, а выполнить его расчет. Для этого необходимо разбить интервал (a, b) на маленькие отрезки длиной h точками xj= a + j·h (j= 0, 1, ..), найти наибольшее значие среди величин  (j= 0, 1, ..) и несколько увеличить его умножением на числовой коэффициент, больший единицы, (на практике - равный не менее 1,25). Эта величина может быть тспользована в качестве М.
(j= 0, 1, ..) и несколько увеличить его умножением на числовой коэффициент, больший единицы, (на практике - равный не менее 1,25). Эта величина может быть тспользована в качестве М.

 | |||||||
 | |||||||
 | |||||||
 |





















