Локальная абсолютная непрерывность вероятных мер. Теорема Гирсанова

§8 Локальная абсолютная непрерывность вероятных мер. Теорема Гирсанова.

8.1. Пусть на фильтрованном измеримом пространстве  заданы две вероятностные меры и Р. Обозначим через  и  сужение вероятностных мер и Р, соответственно, на .

Обозначим .

Определение. Мера  называется локально абсолютно непрерывной относительно меры Р (обозначаем ), если  для каждого n.

Определение. Мера  называется локально эквивалентной мере Р (обозначаем ), если  для каждого n, т.е.  и  для каждого .

Обозначим через - производную Радона - Никодима, которую мы будем называть локальной плотностью. Отметим, что из  не следует .

Теорема 35. Пусть - локальная плотность меры  относительно меры Р. Тогда - мартингал относительно меры Р.

Доказательство. Пусть , имеем
Отсюда в силу произвольности А получаем, что Р - п. н. для  . Доказательство закончено.

Следствие 36. Если  - равномерно интегрируемый неотрицательный мартингал, то существует  - измеримая неотрицательная случайная величина  такая, что  и  Р - п. н. (Это утверждение вытекает из теоремы 6).

Рекомендуемые материалы

2.8.2. Теорема 37 (Гирсанов). Пусть  - локальный мартингал относительно меры Р, а  - локальная плотность меры  относительно меры Р. Пусть  и для любого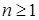

  Р - п. н. Тогда относительно меры  последовательность  определяемая соотношением

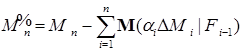
является локальным мартингалом.

Доказательство. Пусть -измеримая случайная величина. Тогда Р - п. н. справедливо равенство

.                                                            (21)

Действительно. Пусть  - любая  измеримая ограниченная случайная величина. Тогда, с одной стороны, имеем

В лекции "СЕРВАНТЕС Сааведра Мигель де" также много полезной информации.

                      (22)

С другой стороны

                  (23)

Из (23) и (22) в силу произвольности  получаем (21). Далее, в силу (21), имеем Р - п. н.

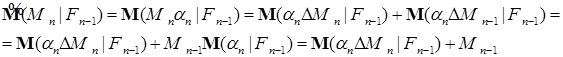
Значит является мартингал-разностью относительно меры . Доказательство закончено.