Подпространства и линейные оболочки

Подпространства и линейные оболочки

Определение 1.3  Подмножество  линейного пространства  называется подпространством пространства , если вместе с любыми двумя векторами оно содержит их сумму, а вместе с любым вектором - результат умножения его на любое число.

Утверждение 1.1  Подмножество  линейного пространства  является подпространством  тогда и только тогда, когда для любой системы векторов в оно содержит их произвольную линейную комбинацию.

Доказательство. Упражнение.

Примеры. 1) В пространстве всех геометрических векторов подмножество всех векторов, параллельных некоторой плоскости, будет подпространством, а подмножество всех векторов, концы которых лежат на некоторой плоскости, не будет подпространством.

2) Множество всех решений однородной линейной системы есть, как мы видели в первом семестре, векторное пространство, которое будет ни чем иным, как подпространством арифметического пространства  (где  в данном случае есть число неизвестных системы).

3) В пространстве  рассмотрим подмножество всех многочленов степени, не превосходящей некоторого фиксированного . Сумма любых двух таких многочленов снова есть многочлен из заданного множества, равно как и результат умножения такого многочлена на произвольное число остается в данном множестве многочленов. Следовательно, множество многочленов степени не выше  является  подпространством  пространства . Можно доказать, что система многочленов является базисом этого подпространства (упражнение!), и, таким образом, размерность данного подпространства многочленов равна . Мы имеем здесь, стало быть, пример конечномерного подпространства  бесконечномерного линейного пространства.

Определение 1.4   Линейной оболочкой системы векторов  некоторого линейного пространства  называется множество всех линейных комбинаций векторов системы.

Линейную оболочку будем обозначать . По определению тогда

Рекомендуемые материалы

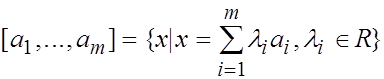
В первом семестре мы определили понятие ранга системы векторов как наибольшего числа линейно независимых векторов системы. Нетрудно доказать следующий результат:

Лекция "Решение проблемы" также может быть Вам полезна.

Утверждение 1.2  Ранг системы векторов равен размерности ее линейной оболочки.

Примеры. 1) В пространстве геометрических векторов возьмем систему векторов, состоящую из некоторых двух ненулевых и неколлинеарных векторов . Тогда (для произвольных вещественных  и ). Геометрически это множество векторов, параллельных плоскости векторов  (любые два неколлинеарных вектора могут быть «положены» в некоторую плоскость, определенную однозначно с точностью до параллельного

переноса) - см. рис. 1.1.

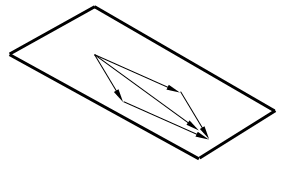
Рис. 1.1

2) Пространство многочленов, рассмотренное выше, есть линейная оболочка системы степенных функций .