Неориентированные графы - основные определения
Неориентированные графы
Основные определения
Пусть V – конечное множество некоторых элементов, и IV – его тождественное отношение, такое, что:
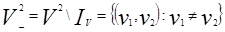
Обозначим
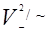Определим отношение эквивалентности следующим образом:
(v1,v2) ~ (w1,w2), если (v1,v2) = (w1,w2) или (v1,v2) = (w2,w1). Множество эквивалентных классов, определенное таким образом, обозначим
Каждый класс эквивалентности содержит два элемента, так как если
, то [(v1,v2)] = {(v1,v2), (v2,v1)}.
Рекомендуемые материалы
Графом называется упорядоченная пара G = (V, E), где V – непустое конечное множество вершин, а , то есть E - это множество неупорядоченных пар различных вершин.
Множество E - это множество ребер графа. Обычно в графе всегда можно определить количество вершин |V| и ребер |E|.
Граф G определяет нерефлексивное, симметричное отношение на множестве V. Обратное утверждение тоже верно: нерефлексивное, симметричное отношение на множестве V определяет граф.
Изображение графа G = (V, E) получается путем расположения различных точек на R2 для каждой вершины v Î V . Причем, если [v, w] Î E, проводим линию, соединяющую вершины v и w.
Графы в значительной мере выражают отношения между вершинами, а не их расположение в пространстве. То есть один и тот же граф может быть изображен разными способами (рис. 1).
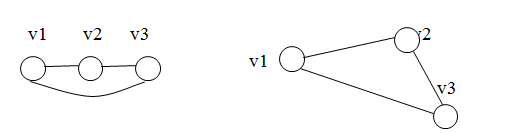
Рис. 1. Примеры изображения графа
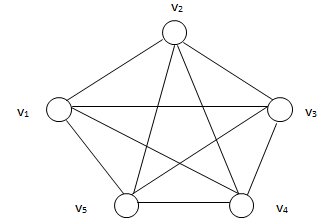
Приведем пример построения графа (рис. 2).
Пусть V={1, 2, 3, 4, 5}.
Тогда IV = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}.
V2 = V ´ V = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
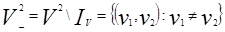
= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}
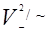
= {[(v1, v2)], [(v1, v3)], [(v1, v4)], [(v1, v5)],
[(v2, v1)], [(v2, v3)], [(v2, v4)], [(v2, v5)],
[(v3, v1)], [(v3, v2)], [(v3, v4)], [(v3, v5)],
[(v4, v1)], [(v4, v2)], [(v4, v3)], [(v4, v5)],
[(v5, v1)], [(v5, v2)], [(v5, v3)], [(v5, v4)]}.
По определению 
. Следовательно, может быть, что 
. В результате получили граф G = (V, E), причем такой, что |V| = 5, |E| = 20.
Вам также может быть полезна лекция "Координаты исследования историко-литературного процесса".
Рис. 2 . Полный граф
Граф H = (V1, E1) является подграфом графа G = (V, E), если V1 Í V и E1 Í E.
Если V1 = V, то граф H является остовным подграфом графа G. Если V1 – непустое подмножество вершин графа (V, E), то подграф (V1, E1), порожденный V1, определяется как
[v, w] Î E1 Û v, w Î V1 и [v, w] Î E.
Граф G = (V, E) называется полным, если для всех v1, v2 Î V имеем [v1, v2] Î E. Полный граф с n вершинами обозначается Kn.
Граф G = (V, E) называется двудольным, если существует разбиение множества его вершин V = {V1, V2} такое, что никакие две вершины из V1 или из V2 не являются смежными. Двудольный граф называется полным, если для любой пары v1 Î V, v2 Î V имеем [v1, v2] Î E. Если |V1| = m и |V2| = n, то полный двудольный граф G = (V, E) обозначается Km,n.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
