Определение основных элементарных функций. Формула Эйлера
§7. Определение основных элементарных функций. Формула Эйлера.
Рассмотрим степенной ряд 
Если z − действительная переменная, то он представляет
собой разложение функции 
в ряд Маклорена и, следовательно, удовлетворяет
характеристическому свойству показательной функции: 
, т.е. 
. Это и является основанием для определения экспоненциальной функции в комплексной области :
Определение 1. 
.
Аналогично определяются функции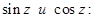 
Определение 2.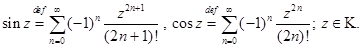 
Все три ряда сходятся абсолютно и равномерно в любой ограниченной замкнутой области комплексной плоскости.
Из трех полученных формул простой подстановкой выводится формула Эйлера:
Рекомендуемые материалы
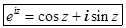
Отсюда сразу получается показательная форма записи комплексных чисел:
Формула Эйлера устанавливает связь между обычной и гиперболической тригонометрией.
Рассмотрим, например, cos z: 
Аналогично получаются остальные соотношения. Итак:
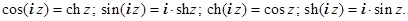
Примеры. Представить указанные выражения в виде 
1. 
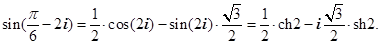
2. 
(выражение в скобках представляет собой число i , записанное в показательной форме)
3.
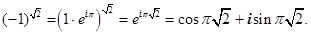
Обратите внимание на лекцию "Часть 5".
4. Найти линейно независимые решения линейного ДУ 2 – го порядка: 
Корни характеристического уравнения равны :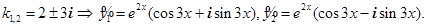 
Так как мы ищем действительные решения уравнения, то в качестве фундаментальной системы решений можно взять функции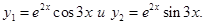 
Определим, в заключение, логарифмическую функцию комплексной переменной. Как и в действительной области, будем считать ее обратной к показательной. Для простоты рассмотрим только экспоненциальную функцию, т.е. решим уравнение 
относительно w , которую и назовем логарифмической функцией. Для этого прологарифмируем уравнение, представив z в показательной форме:
Если вместо arg z написать Arg z (§2), то получим бесконечнозначную функцию 
