Последовательность и ее предел

Лекция 2

Последовательность и ее предел.

Комплексное число называется пределом последовательности:  (или последовательность сходится к точке : ), если

выполнено  .

Теорема. Для того чтобы последовательность  { } необходимо и достаточно .

Доказательство провести самостоятельно, используя неравенство треугольника  ()  и теорему Пифагора  ().

Из теоремы следует, что многие свойства последовательностей действительных чисел могут быть перенесены на последовательности комплексных чисел.

Функция комплексной переменной.

Рекомендуемые материалы

Комплексное число , как всякое комплексное число, имеет действительную и мнимую части . Это – действительная  и мнимая  части функции.

Пример. Выделим действительную и мнимую части функции .

Элементарные функции комплексной переменной.

Экспонента  и при комплексных z сохраняет свои основные свойства

.

Формула Эйлера  справедлива и для комплексных чисел z. Это будет показано позже. Используя четность cosz, chz и нечетность sinz, shz, (для комплексных z это тоже будет показано позже), получим формулы связи экспоненты с с тригонометрическими и гиперболическими синусами и косинусами. . Складывая и вычитая , получим

.

Гиперболические косинус и синус определяются аналогично функциям действительной переменной

.

Отсюда .

Получим формулы связи тригонометрических и гиперболических косинусов и синусов.

Покажем, что функции - функции периодические с периодом .

,

 имеют тот же период , так как они являются линейной комбинацией  - периодических функций с периодом .

Покажем, что функции - функции периодические с периодом .

.

имеют тот же период , так как они являются линейной комбинацией  - периодических функций с периодом .

Упражнение. Выведите формулы

,

используя свойства экспоненты и полученные выше формулы.

Пример. Вычислить sin (+5i), tg ()

sin (+5i) =  sincos5i + cos sin5i = sin5i = ch5

Логарифмическая функция.

Функция  определяется как обратная функция по отношению к функции . Пусть , .

Тогда .

Так как , то, переходя в последнем соотношении к модулям, имеем , . 

Аргументы левой и правой части в соотношении могут отличаться на , поэтому . Поэтому

.

Это – многозначная функция. Ее главная ветвь

 - функция однозначная.

Пример. Вычислить ln(-1),  Ln(-1), ln(1+i).

Ln(-1) = ln |-1| + iarg (-1) + = +,  ln(-1) =

ln(1+i) = ln|1+i| + iarg(1+i) = .

Предел и непрерывность функции.

Комплексное число b называется пределом функции f(z) при ,

.

Это определение – то же, что определение предела функции действительной переменной с той лишь разницей, что модуль здесь имеет смысл расстояния на комплексной плоскости, а не на действительной прямой, как раньше. Кроме того, окрестность точки – не интервал с центром в этой точке, а круг без границы с центром в этой точке.

Функция  называется непрерывной в точке , если .

Функция  называется непрерывной в области G, если она непрерывна в каждой точке этой области.

Область M называется областью однолистности функции , если

Линейная функция  осуществляет линейное отображение комплексной плоскости на себя. . Отсюда видно, что линейное отображение сводится к растяжению в  раз и повороту на  комплексной плоскости. Здесь область однолистности – вся плоскость.

Инверсия  () переводит все точки, лежащие вне единичной окружности  внутрь и наоборот. Точки  остаются на месте, единичная окружность отображается на себя.

Отображение  () часть действительной оси () и верхнюю полуплоскость отображает на всю плоскость. Часть действительной оси () и нижняя полуплоскость тоже отображаются на всю плоскость. Здесь две области однолистности. Поэтому  обратная функция двузначна.

Упражнение. Покажите, что при отображении  существует n областей однолистности. Выделите их. Функция поэтому n – значна.

Отображение  переводит прямую, параллельную мнимой оси ( ) в  - окружность с центром в начале координат, радиусом . Прямая, параллельная действительной оси  переводится в  - луч из начала координат под углом y к действительной оси.

Поэтому полоса размером вдоль действительной оси переводится во всю плоскость и представляет собой область однолистности  (каждый отрезок в полосе, параллельный мнимой оси (x = a) отобразится в окружность радиуса a с центром в начале координат, меняя a, заполним этими окружностями всю плоскость). Следовательно, здесь бесконечное количество областей однолистности, а обратная функция - бесконечнозначна.

Производная функции комплексной переменной вводится так же, как и для функции действительной переменной

.

Функция  называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде

, то есть  - бесконечно малая при . Главная линейная относительно  часть приращения функции в точке ,  называется дифференциалом функции в точке , ().

Замечание. Функция двух переменных  называется дифференцируемой в точке (), если ее приращение в этой точке можно представить в виде

++,

где ,  - бесконечно малые при ,

,  .

Теорема. Для того, чтобы функция  была дифференцируема в точке , необходимо и достаточно, чтобы существовала ее конечная производная в этой точке.

Доказательство. Проводится так же, как и для функции действительной переменной с использованием теоремы о связи функции, предела и бесконечно малой.

Необходимость. Пусть функция дифференцируема в точке , тогда

,

Делим обе части на

. Так как  - бесконечно малая при , то по теореме о связи функции, ее предела и бесконечно малой, .

Поэтому  - формула для вычисления дифференциала.

Достаточность. Пусть в точке  существует конечная производная функции . Тогда по теореме о связи функции, предела и бесконечно малой . Умножая на , получим . Следовательно, функция дифференцируема в точке .

Функция называется дифференцируемой в области, если она дифференцируема в каждой точке этой области.

Теорема (Коши – Римана). Для того, чтобы функция  была дифференцируема в точке , необходимо и достаточно, чтобы ее действительная и мнимая части , были бы дифференцируемы в этой точке как функции двух переменных и в этой точке выполнялись бы условия Коши – Римана

, причем .

Замечание. С учетом условий Коши – Римана производная функции в точке может быть записана так: ==

==

Необходимость. Пусть функция дифференцируема в точке z_0. Тогда

.

Пусть  , .

.

Отделяя действительную и мнимую части, имеем:

,

.

Следовательно, функции дифференцируемы в точке

Из первого соотношения следует, что

.

Из второго соотношения следует, что

, .

Поэтому . .

Достаточность. Пусть функции дифференцируемы в точке и выполняются условия Коши – Римана.

где  - бесконечно малые при .

.

Функции - бесконечно малые при , поэтому они являются бесконечно малыми при . Справедливы неравенства . Поэтому отношения приращений в двух последних скобках – ограниченные величины. Следовательно, выражения в двух последних скобках – бесконечно малые величины при  как произведения бесконечно малых на ограниченные. Обозначим два последних слагаемых  - бесконечно малая при .

.

Умножая это выражение на , получим

.

Следовательно, функция дифференцируема в точке .

Условия Коши – Римана позволяют легко проверить дифференцируемость функции в точке.

Функция называется аналитической в области, если она дифференцируема в области.

Функция называется аналитической в точке, если она дифференцируема в этой точке и некоторой ее окрестности.

Основные элементарные функции  аналитические на всей комплексной плоскости.

Проверим, например, условия Коши – Римана для функции

Ещё посмотрите лекцию "КЛЮЧЕВСКИЙ Василий Осипович" по этой теме.

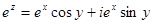
 Условия Коши – Римана выполнены при любых значениях переменных, функция аналитическая во всей комплексной плоскости.

Пример. Функция z = x не является дифференцируемой ни в одной точке, так как .

Пример Функция .

. Функция дифференцируема только в точке z=0 и более ни в одной точке. Она не аналитическая ни в одной точке, поскольку для аналитичности кроме дифференцируемости в точке нужна еще дифференцируемость в некоторой области.

Пример. не является дифференцируемой ни в одной точке, так как условия Коши – Римана не выполнены, .