Формула Тейлора с остаточным членом в форме Пеано, Лагранджа

Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.

Теорема. Пусть ф-ция F(x) определена в  и имеет в  производные до (n+1)-го порядка включительно. Пусть x – произвольное значение аргумента ф-ции из , тогда для произвольного значения P, p>0 , расположенная между a и x, такие что справедлива следующая формула: .  . Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде.

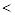
 эта функция – многочлен степени n – многочлен Тейлора с центром в точке а.

Обозначим . Рассмотрим вспомогательную функцию .

, где  Покажем, что на [a;x] удовлетворяет всем условиям теоремы Ролля:

1) непрерывность на [a;x];

2) дифференцируема на (a;x);

3)  

; ;    ;  

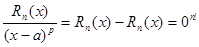
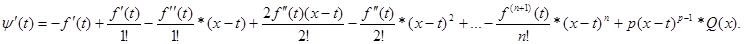
Рекомендуемые материалы

Теорема. Остаточный член в форме Тейлора представляет собой б. м. более высокого порядка малости, чем  при . , .

Доказать: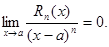

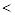
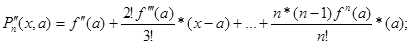
;   =0; ;   n раз применяем пр. Б-Л.=

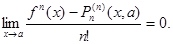
Бесплатная лекция: "Лекция 3" также доступна.

Такую запись остаточного члена называют ост. Чл. В форме Пеано: .

Рассмотрим другие формы записи остаточного члена. ,  

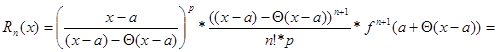
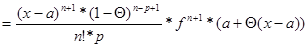
1) p=n+1, тогда  - остаточный член в форме Лагранжа.

2) p=1 – в форме Коши:   Число  в формуле Лагранжа и формуле Коши разные, т. К. зависят от P. Остаточный член в форме Лагранжа и Коши представляют собой погрешность, которую мы получаем, заменяя функцию f(x) ее многочленом Тейлора. Если нас интересует порядок малости такой замены при , то он совпадает с порядком малости остаточного члена в форме Пеано.

Оценка остаточного члена в форме Лагранжа.

Пусть функция имеет производную любого порядка в  и эти производные ограничены одной и той же константой M.  ;