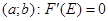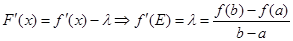Доказать теорему Лагранжа
2020-06-032021-03-09zzyxelСтудИзба
Доказать теорему Лагранжа.
Пусть функция 
.
1. Определена и непрерывна на отрезке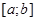 
.
2. Дифференцируема на интервале 
.
Тогда существует 
из интервала 
.
"6.2. Ламинарное движение жидкости" - тут тоже много полезного для Вас.
Доказательство: Рассмотрим вспомогательную функцию 
, где 
- константа.
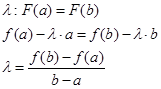
1. Она непрерывна на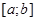
2. дифференцируема на .
Все условия теоремы Ролля выполняются 
существует из 
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
