Конформные отображения
Конформные отображения
Опр. Отображение обладающие свойствами консерватизма углов и постоянства растяжений называется конформным.
Теорема. Если  аналитическая функция в области G
аналитическая функция в области G  в G, то
в G, то  задает конформное отображение области G.
задает конформное отображение области G.
Док-во:
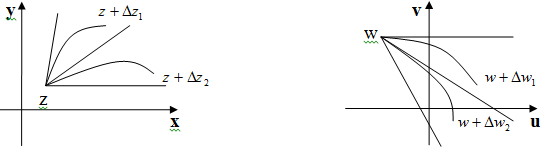
 ;
;  ;
;
 ;
;  ;
;
Рекомендуемые материалы
 - постоянство растяжений.
- постоянство растяжений.
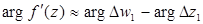
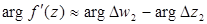
 - консерватизм углов.
- консерватизм углов.
Доказано.
1. Линейная функция.
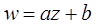
1)  - параллельный перенос.
- параллельный перенос.
2) 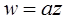
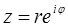
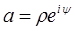
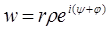
При линейном преобразовании прямые переходят в прямые, окружность переходит в окружность.
2. Дробно-линейная функция.

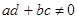
 , т.е. дробно-линейное преобразование сводится к линейному и функции
, т.е. дробно-линейное преобразование сводится к линейному и функции  .
.
Опр. Обобщенная окружность:
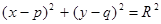
 , т.е. это окружность или прямая.
, т.е. это окружность или прямая.
Теорема. Дробно-линейная функция отображает обобщенную окружность в обобщенную окружность.
Док-во:
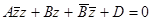

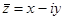
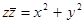
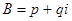
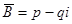
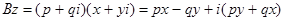
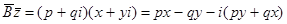
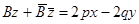
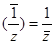

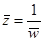
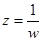
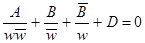
 - обобщенная окружность.
- обобщенная окружность.
Опр. Точки B и С - сопряженные относительно окружности Г, если любая окружность  , проходящая через эти точки, ортогональна Г.
, проходящая через эти точки, ортогональна Г.
Лемма. Если точки В и С явл. Сопряженными относительно окр-ти с центром О, А-точка пересечения Г и  ., то
., то  .
.
Утв. Если  дробно – линейное отображение, то
дробно – линейное отображение, то  переводит точки, сопряженные относительно окружности, в точки, сопряженные относительно ее образа.
переводит точки, сопряженные относительно окружности, в точки, сопряженные относительно ее образа.
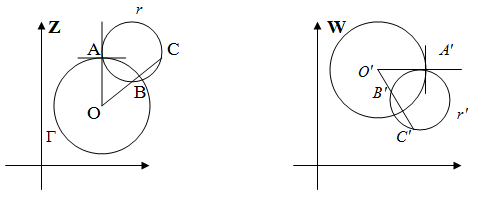
 ;
; 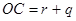
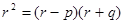
 , т.е. сопряженными являются точки 0 и
, т.е. сопряженными являются точки 0 и  .
.
Примеры решения задач:
Задача 1.
Отобразить полуокружность в единичный круг.
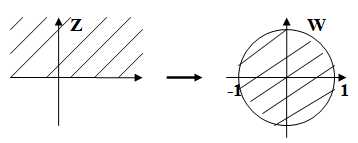
Решение:

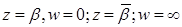
 и
и  сопряженные относительно Ох, т.е. действительная ось отображается в окружность.
сопряженные относительно Ох, т.е. действительная ось отображается в окружность.
 ;
; 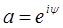
 - искомое отображение.
- искомое отображение.
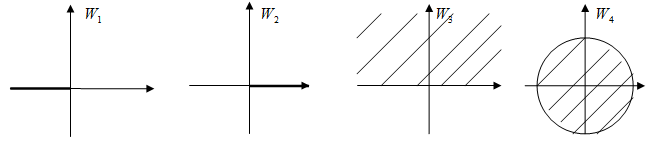
Задача 2.
Отобразить отрезок в единичный круг.
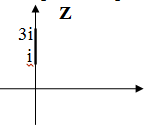
Решение:
 - отобразить отрезок в
- отобразить отрезок в  ;
;
 ;
;
 ;
;
 ;
;
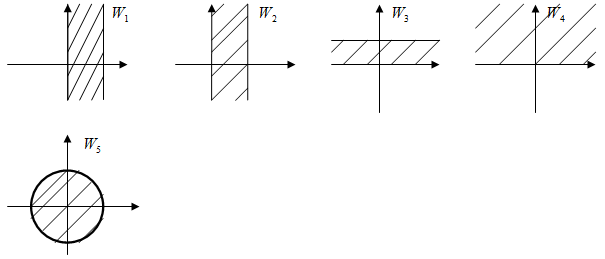
Задача 3.
Отобразить полосу в единичный круг.
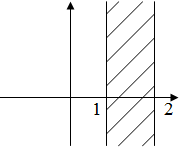
Решение:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Функция Жуковского
 ;
; 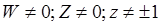
 ;
;
 ;
;
 ,
,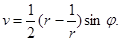
Ещё посмотрите лекцию "87 Криволинейные интегралы" по этой теме.
1)  - эллипс
- эллипс 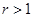

2) 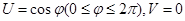
 - функция, обратная функции Жуковского.
- функция, обратная функции Жуковского.
Теорема Римана
Если G – односвязная область, граница которой состоит более чем из одной точки, то существует аналитическая функция, задающая конформное отображение G на единичный круг.

















