Определение определённого интеграла
11.1. Определение.
11.1.1. Вычисление площади криволинейной трапеции. Пусть на отрезке 
 задана непрерывная функция
задана непрерывная функция  , принимающая на этом отрезке неотрицательные значения :
, принимающая на этом отрезке неотрицательные значения :  при
при  . Требуется определить площадь
. Требуется определить площадь  трапеции
трапеции  , ограниченной снизу отрезком
, ограниченной снизу отрезком  , слева и справа - прямыми
, слева и справа - прямыми  и
и  , сверху - функцией
, сверху - функцией  .
.
 |
Для решения этой задачи разделим произвольным образом основание
 фигуры точками
фигуры точками 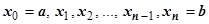 на
на 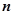 частей
частей 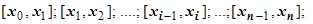 символом
символом 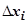 будем обозначать длину
будем обозначать длину 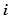 -го отрезка:
-го отрезка: 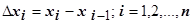 . На каждом из отрезков
. На каждом из отрезков 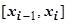 выберем произвольную точку
выберем произвольную точку 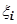 , найдём
, найдём 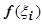 , вычислим произведение
, вычислим произведение 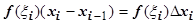 (это произведение равно площади прямоугольника
(это произведение равно площади прямоугольника 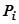 с основанием
с основанием 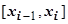 и высотой
и высотой 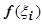 ) и просуммируем эти произведения по всем прямоугольникам. Полученную сумму обозначим
) и просуммируем эти произведения по всем прямоугольникам. Полученную сумму обозначим 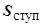 :
: 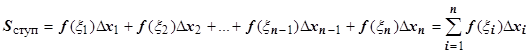 .
. 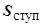 равно площади ступенчатой фигуры, образованной прямоугольниками
равно площади ступенчатой фигуры, образованной прямоугольниками 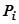 ,
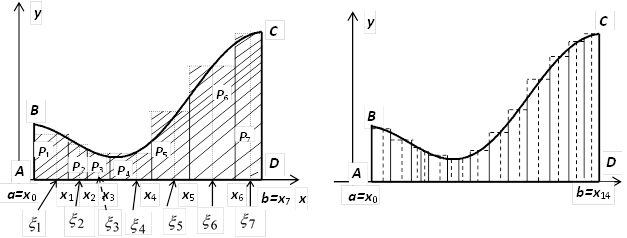
,  ; на левом рисунке эта площадь заштрихована.
; на левом рисунке эта площадь заштрихована. 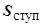 не равна искомой площади
не равна искомой площади  , она только даёт некоторое приближение к
, она только даёт некоторое приближение к  . Для того, чтобы улучшить это приближение, будем увеличивать количество
. Для того, чтобы улучшить это приближение, будем увеличивать количество 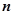 отрезков таким образом, чтобы максимальная длина этих отрезков
отрезков таким образом, чтобы максимальная длина этих отрезков  стремилась к нулю (на рисунке ступенчатые фигуры изображены при
стремилась к нулю (на рисунке ступенчатые фигуры изображены при  (слева) и при
(слева) и при  (справа)). При
(справа)). При  разница между
разница между 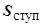 и
и  будет тоже стремиться к нулю, т.е.
будет тоже стремиться к нулю, т.е.
 .
.
11.1.2. Определение определённого интеграла. Пусть на отрезке  задана функция
задана функция  . Разобьём отрезок
. Разобьём отрезок  произвольным образом на
произвольным образом на 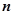 частей точками
частей точками 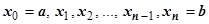 ; длину
; длину 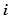 -го отрезка обозначим
-го отрезка обозначим 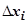 :
: 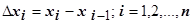 ; максимальную из длин отрезков обозначим
; максимальную из длин отрезков обозначим  . На каждом из отрезков
. На каждом из отрезков 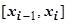 выберем произвольную точку
выберем произвольную точку 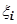 и составим сумму
и составим сумму  .
.
Сумма  называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм
называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм  при
при  , не зависящий ни от способа разбиения отрезка
, не зависящий ни от способа разбиения отрезка  на части
на части 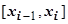 , ни от выбора точек
, ни от выбора точек 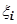 , то функция
, то функция  называется интегрируемой по отрезку
называется интегрируемой по отрезку  , а этот предел называется определённым интегралом от функции
, а этот предел называется определённым интегралом от функции  по отрезку
по отрезку  и обозначается
и обозначается
 .
.
"16 Культура России XVII века" - тут тоже много полезного для Вас.
Функция  , как и в случае неопределённого интеграла, называется подынтегральной, числа
, как и в случае неопределённого интеграла, называется подынтегральной, числа  и
и  - соответственно, нижним и верхним пределами интегрирования. Кратко определение иногда записывают так:
- соответственно, нижним и верхним пределами интегрирования. Кратко определение иногда записывают так:  .
.
В этом определении предполагается, что  . Для других случаев примем, тоже по определению:
. Для других случаев примем, тоже по определению:
Если  , то
, то  ; если
; если  , то
, то  .
.
11.1.3. Теорема существования определённого интеграла. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема по этому отрезку.
, то она интегрируема по этому отрезку.
Примем это утверждение без доказательства, поясним только его смысл. Интегрируемость функции означает существование конечного предела последовательности интегральных сумм, т.е. такого числа  , что для любого
, что для любого  найдётся такое число
найдётся такое число  , что как только разбиение отрезка удовлетворяет неравенству
, что как только разбиение отрезка удовлетворяет неравенству  , то, независимо от выбора точек
, то, независимо от выбора точек 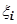 ,
,  . Требование непрерывности
. Требование непрерывности  достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на
достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на  при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если
при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если  неограничена на
неограничена на  , то она неограничена на каком-либо
, то она неограничена на каком-либо 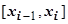 , т.е. на этом отрезке можно найти такую точку
, т.е. на этом отрезке можно найти такую точку 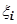 , что слагаемое
, что слагаемое  , а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).
, а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).
11.1.4. Геометрический смысл определённого интеграла. Как следует из пункта 11.1.1, если  на отрезке
на отрезке  , то
, то  равен площади криволинейной трапеции
равен площади криволинейной трапеции  , ограниченной снизу отрезком
, ограниченной снизу отрезком  , слева и справа - прямыми
, слева и справа - прямыми  и
и  , сверху - функцией
, сверху - функцией  .
.



















