Формула Тейлора

Формула Тейлора

            Теорема 2.7. Если функция  есть функция класса  для некоторого открытого множества , то для любой точки  найдется такая ее окрестность (содержащаяся в ), что приращение функции в этой окрестности представимо в виде:

               (1)

            Перед доказательством теоремы заметим следующее. Формула (1) называется формулой Тейлора для числовой функции векторного аргумента. Она вполне аналогична формуле Тейлора из одномерного анализа. При она дает обычную форму приращения дифференцируемой в точке функции:

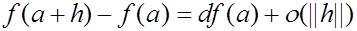
(см. формулу (3) п. 2.5).

            При  имеем:

(2)

Эта формула (2) особенно важна при исследовании функций на экстремум.

Рекомендуемые материалы

            Переходим к доказательству теоремы. Мы проведем его в два этапа: сначала мы дадим новый вывод формулы Тейлора в одномерном случае и получим эту формулу с остаточным членом в интегральной форме.            Затем мы сведем вывод в векторном случае к полученному одномерному результату. Мы не сможем вполне строго и подробно доказать оценку остаточного члена в общем случае, так как для этого требуется более подробное рассмотрение высших производных.

            Доказательство теоремы 2.7. 1) Вывод одномерной формулы Тейлора с остаточным членом в интегральной форме. В предположении, что функция  дифференцируема на отрезке  преобразуем интеграл

            ,

используя интегрирование по частям при :

            (3)

            Пусть функция дифференцируема на отрезке   раз, причем -ая производная функции непрерывна на . Тогда, используя формулу (3), вычислим:

Итак, полагая  и обозначая через  последний интеграл в написанной выше цепочке выкладок, получим

                     (4)            Это и есть искомый вид одномерной формулы Тейлора с остаточным членом в интегральной форме.         

            Для оценки остаточного члена воспользуемся обобщенной теоремой об оценке (это возможно ввиду непрерывности -ой производной!):

            ,

где  - наименьшее (наибольшее) значение непрерывной функции на отрезке .

            Но очевидно, что . Следовательно,

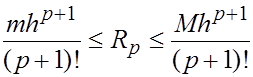
            Это значит, что модуль остаточного члена имеет порядок , или . Таким образом, мы пришли к остаточному члену в форме Пеано.

            Применяя же к интегралу  обобщенную теорему о среднем, будем иметь:,

где  ( - точка интервала ). Последнее выражение представляет собой, как известно, остаточный член в форме Коши.

            Итак, для достаточно гладкой функции замена ее приращения суммой в (4) с отбрасыванием остаточного члена дает ошибку, которая есть бесконечно малая высшего порядка по сравнению с приращением аргумента, возведенного в «степень гладкости» функции.

            2) Вывод формулы Тейлора для числовой функции векторного аргумента.

            Фиксировав точку  и вектор , рассмотрим приращение функции в окрестности точки в виде:

            , где .

            Поскольку  и  фиксированы, мы можем считать это приращение функцией вещественного аргумента . Обозначим   и применим к функции только что выведенную формулу Тейлора (4), в которой :

            ,                  (5)

где .

            Конечно, еще нужно вычислить производные функции , обосновав тем самым их существование. Прежде всего, заметим, что эта функция есть сложная функция вещественного переменного , так как она ( зависит от  не непосредственно, а через вектор  (геометрически любой такой вектор  можно представить очень наглядно - это вектор, конец которого лежит на отрезке, соединяющем точки  и  (см. рис. 2.14).

                                   a          x          a+h

                                   Рис. 2.14

            Тогда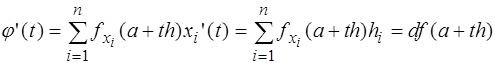

т.е. первая производная функции  равна первому дифференциалу функции в текущей точке .

            Совершенно аналогично

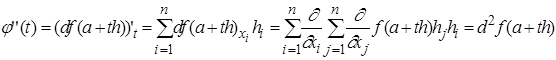
Индукцией по  легко доказать формулу:

Так как по условию , то функция  имеет на отрезке  все производные до -ой включительно, и последняя производная непрерывна на отрезке. Таким образом, разложение (5) корректно.

Кроме того, очевидно, что

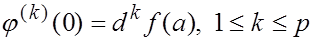
Следовательно, поскольку , а , мы получаем:

            ,       (6)

где  .

            В силу непрерывности -ого дифференциала остаточный член можно оценить, используя обобщенную теорему о среднем:

            ,                             (7)

где .

            Модули первых двух дифференциалов оценить легко:

            ,

(при оценке второго дифференциала мы использовали неравенство Коши-Буняковского!).

            Можно доказать (это доказательство не приводится), что и в общем случае имеет место оценка:

(интуитивно это понятно из записи степенной формы для дифференциала высшего порядка - см. п. 2.10).

Рекомендуем посмотреть лекцию "11.1 Казахстан в годы Великой Отечественной войны".

            Итак, для остаточного члена (7) можно записать

            ,

а формулу (6) - переписать в виде:

            Мы получили формулу (1) и тем самым полностью доказали теорему 2.7.