Обобщенная постановка первой смешанной задачи для параболического уравнения
§12. Обобщенная постановка первой смешанной задачи для параболического уравнения.
Здесь ограничимся однородными краевыми условиями. Для них удается доказать теорему о существовании и единственности решения в произвольной области, ограниченной или неограниченной.
Будем рассматривать в цилиндрической области  , параболическое уравнение второго порядка:
, параболическое уравнение второго порядка:
 . (1)
. (1)
Коэффициенты уравнения для почти всех  из области
из области  удовлетворяют условию равномерной эллиптичности
удовлетворяют условию равномерной эллиптичности
 , (2)
, (2)
с положительными постоянными  и Г. Ищется решение
и Г. Ищется решение  уравнения (1), удовлетворяющее краевому условию:
уравнения (1), удовлетворяющее краевому условию:
 (3)
(3)
и начальному условию
Рекомендуемые материалы
 . (4)
. (4)
Для определения обобщенного решения задачи (1), (3), (4) понадобятся пространства
 и
и  .
.
Введем обозначения  .
.
Рассмотрим отображение  , действующее по формуле:
, действующее по формуле:
 .
.
Замыкание образа этого отображения и есть пространство  . Как и раньше, нетрудно установить, что элемент
. Как и раньше, нетрудно установить, что элемент
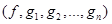
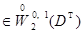
однозначно восстанавливается по координате 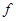 : элементы
: элементы  являются обобщенными, производными по
являются обобщенными, производными по  для
для  . Следует отметить, что
. Следует отметить, что 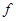 может не иметь производную по
может не иметь производную по  .
.
Чтобы определить пространство  , рассмотрим отображение
, рассмотрим отображение  , действующее по формуле
, действующее по формуле
 .
.
Пространство  определяется как замыкание образа этого
определяется как замыкание образа этого
отображения. Норма в этом пространстве определяется формулой:
 . (5)
. (5)
Определение.
Обобщенным решением задачи (1), (3), (4) в  называется функция
называется функция  , удовлетворяющая интегральному тождеству:
, удовлетворяющая интегральному тождеству:
 (6)
(6)
при любой функции  , такой, что
, такой, что  .
.
Для доказательства единственности обобщенного решения задачи (1), (3), (4) установим следующее его свойство.
Теорема 1.
Обобщенное решение задачи (1), (3), (4) принадлежит классу  и удовлетворяет энергетическому тождеству:
и удовлетворяет энергетическому тождеству:
 (7)
(7)
при всех  .
.
Напомним, что функции  и являются элементом
и являются элементом  , которые представляют собой классы эквивалентных функций. Принадлежность этого элемента классу
, которые представляют собой классы эквивалентных функций. Принадлежность этого элемента классу  означает наличие такой функции
означает наличие такой функции  в классе эквивалентности этого элемента, для которой определенно отображение
в классе эквивалентности этого элемента, для которой определенно отображение  и оно непрерывно для всех
и оно непрерывно для всех  .
.
Для доказательства теоремы будет использоваться осреднение Стеклова. Оно определяется формулой:
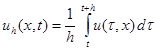
для любой непрерывной функции. Установим ряд свойств осреднения Стеклова.
Свойства осреднения Стеклова:
1
 .
.
Доказательство.
 .
.
После смены порядков интегрирования по  и
и  будем иметь
будем иметь
 .
.
Поскольку установлена ограниченность оператора Стеклова в пространстве  , то он определен не только на плотном множестве, которое составляют непрерывные функции, но и во всем пространстве
, то он определен не только на плотном множестве, которое составляют непрерывные функции, но и во всем пространстве  .
.
2
 в
в  при
при 
 .
.
Ввиду непрерывности оператора Стеклова, достаточно провести доказательство для функций  .
.
 Далее, интегрируя
Далее, интегрируя
 ,
,
после замены переменной  , будем иметь
, будем иметь
 при
при  .
.
3 Если
Если 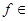
 имеет обобщенную производную
имеет обобщенную производную 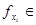
 , то
, то  . Это свойство для гладких функций очевидно, а для негладких устанавливается по непрерывности осреднения Стеклова.
. Это свойство для гладких функций очевидно, а для негладких устанавливается по непрерывности осреднения Стеклова.
4
 .
.
5
 .
.
Доказательство.
 .
.
После смены порядка интегрирования по  и
и  , получим
, получим
 .
.
Лемма 1.
Если 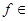
 имеет обобщенную производную
имеет обобщенную производную 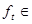
 , то
, то  . Доказательство проведем сначала для
. Доказательство проведем сначала для  .
.
Тогда  .
.
Отсюда, по неравенству Коши-Буняковского
 (8)
(8)
Это неравенство влечет равномерную непрерывность отображения  в
в  .
.
Пусть теперь  – произвольная функция. Тогда найдется последовательность
– произвольная функция. Тогда найдется последовательность  , сходящаяся к
, сходящаяся к  в
в  при
при  .
.
Функции 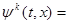
 сходятся к
сходятся к  в
в  при каждом фиксированном
при каждом фиксированном  , поэтому функция
, поэтому функция 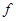 и в этом случае удовлетворяет неравенству (8) .
и в этом случае удовлетворяет неравенству (8) .
Лемма доказана.
Следствие. Если 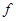
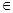
 , то при
, то при 
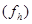
 и
и  .
.
Приступим к доказательству теоремы 1.
Возьмем функцию  . Продолжим ее нулем для значений
. Продолжим ее нулем для значений  . Тогда функция
. Тогда функция  будет принадлежать
будет принадлежать  и удовлетворять
и удовлетворять  .
.
Подставим эту функцию в тождество (6):
 . (9)
. (9)
Тогда по свойству 5 ,
,
 . (10)
. (10)
Далее,
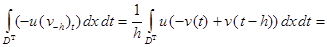
 . (11)
. (11)
Соотношение (9) принимает вид:
 . (12)
. (12)
Последнее справедливо при всех  .
.
Лемма 2.
 в
в  при
при  равномерно по
равномерно по  .
.
Доказательство.
По свойству 2
 в
в  при
при  . Далее выберем конкретный представитель
. Далее выберем конкретный представитель  из класса эквивалентности элемента
из класса эквивалентности элемента 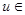
 . Тогда по теореме Фубини:
. Тогда по теореме Фубини:
 .
.
Это означает, что при почти всех  функция
функция  является элементом
является элементом  .
.
Опять по теореме Фубини при  имеем:
имеем:
 . (13)
. (13)
Будем доказывать равномерную фундаментальность последовательности  в
в  для
для  . Для этого подставим в (12)
. Для этого подставим в (12)  и вычтем два получившихся тождества:
и вычтем два получившихся тождества:
 . (14)
. (14)
Поскольку 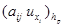
 в
в  , то эта последовательность фундаментальна в
, то эта последовательность фундаментальна в  , поэтому
, поэтому  из (14) следует существование
из (14) следует существование  такого, что при
такого, что при  справедливо неравенство:
справедливо неравенство:
 . (15)
. (15)
Выберем в (14)  при
при  , равную нулю вне
, равную нулю вне  . Тогда
. Тогда
 .
.
Тогда  .
.
Проинтегрируем последнее по  :
:
Рекомендация для Вас - Экологическая ситуация в России и пути оздоровления экологического состояния.
 .
.
Отсюда из фундаментальности  в
в  следует равномерная по
следует равномерная по  фундаментальность
фундаментальность  в
в  .
.
Следовательно,  .
.
Переходя в (13) к пределу по  , получим:
, получим:
 .
.
Следовательно,  .
.






















