Методы спуска

Методы спуска

По аналогии с методами спуска для системы линейных уравнений заменим задачу решения системы    (7) задачей минимизации функции .

Идея методов спуска:

1) Выбирается начальное приближение ;

2) Выбирается направление, в котором  убывает;

3) В этом направлении от  выбирается следующее приближение ;

4) По рекуррентной формуле последовательно находят приближения ,…,;

5) Последнее приближение .

1 способ) Покоординатный спуск

Рекомендуемые материалы

Пусть .

Подставим в  значения всех координат , кроме первой переменной.

Получим функцию от одной переменной. Найдем ее точку минимума. Это будет x₁(1).

Затем  подставим в  x₁(1) и значения всех остальных координат , кроме второй переменной.

Получим функцию от одной переменной. Найдем ее точку минимума. Это будет x₁(2). Продолжая таким образом, получим . И т.д.

Проиллюстрируем поведение алгоритма для m = 2.

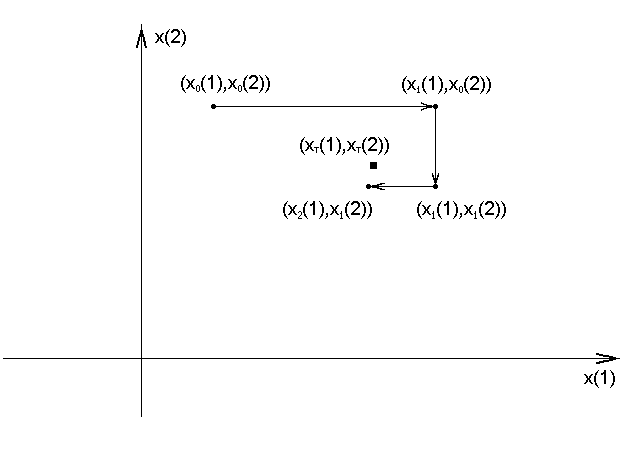
Модификации алгоритма:

1) Случайный покоординатный спуск — порядок переменных выбирается случайным образом.

2) "Метод муравьиной кучи" — покоординатный спуск выполняется для нескольких разных нулевых приближений.

Недостатки алгоритма:

1) Не гарантирует сходимости.

2) Не гарантирует приближение к глобальному экстремуму.

2 способ) Метод наискорейшего спуска.

Использует рекуррентную формулу , где  – некоторый параметр, определяемый из условия:

Бесплатная лекция: "35 Провозглашение независимости Республики Беларусь" также доступна.

.

3 способ) Условная минимизация

Задача: Найти точку , в которой достигается минимум , при условиях в виде неравенств или равенств:

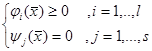
Методы решения таких задач получили название математическое программирование.

Если все функции F, j, y  являются линейными  — линейное  программирование. Если есть нелинейные функции — нелинейное программирование. Если искомое решение должно состоять из целых чисел — целочисленное программирование.