Позиционные игры
Часть II позиционные игры
Во многих практически важных конфликтных ситуациях, располагая той или иной информацией об их прошлом развитии, стороны-участницы совершают свой выбор не раз и навсегда, а последовательно во времени, шаг за шагом. Тем самым, они используют стратегии, отражающие как динамику конфликта, так и степень собственной информированности о фактически складывающейся обстановке в развитии этого конфликта.
1. Структура позиционной игры
Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются так называемые позиционные игры.
Позиционная игра — это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.
Процесс самой игры состоит в последовательном переходе от одного состояния игры к другому состоянию, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом (случайный ход).
В качестве примеров позиционных игр можно привести крестики-нолики, шашки, шахматы, карточные игры, домино и др. Интересно, что право выбора первого хода в этих играх часто определяется случайным образом.
Состояния игры принято называть позициями (отсюда и название — позиционные игры), а возможные выборы в каждой позиции — альтернативами.
Рекомендуемые материалы
Характерной особенностью позиционной игры является возможность представления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры (рис. 1).

Для определенности мы будем рассматривать позиционные игры, в каждой позиции которых, кроме окончательных, ровно две альтернативы — первая и вторая.
Замечание. Символ О, А или В в кружке указывает, кто из игроков (О, А или В) делает очередной ход в заданной позиции. При этом символом О обычно обозначается ход в игре, осуществляемый не игроком, а каким-нибудь случайным механизмом (иногда его называют природой). Например, в позиционной игре, представленной на рис. 1 своим деревом, первый ход производится случайно.
Пользуясь графическим описанием игры, можно сказать, что процесс игры состоит в переходе от начальной позиции к окончательной через непосредственно следующие одна за другой промежуточные позиции.
Каждая окончательная вершина определяет единственную цепь (последовательность идущих друг за другом звеньев), связывающую начальную вершину с данной (рис. 2). Такая цепь называется партией. На рис. 2 одна из партий выделена жирными линиями. Число различных партий равно числу окончательных вершин (позиций).

Рис. 2
В каждой окончательной позиции задан числовой выигрыш игрока А.
Замечание. Мы будем рассматривать здесь только антагонистические позиционные игры.
В шахматах функция выигрышей игрока А (белых) определяется так:
+1 на выигрываемых партиях,
0 на ничейных партиях,
-1 на проигрываемых партиях.
Функция выигрышей игрока В (черных) отличается от функции выигрышей белых только знаком.
Различают позиционные игры с полной информацией и позиционные игры с неполной информацией.
В позиционных играх с полной информацией (пример — шашки, шахматы) каждый игрок при своем ходе знает ту позицию дерева игры, в которой он находится.
В позиционных играх с неполной информацией (пример — домино) игрок, де
лающий ход, не знает точно, в какой именно позиции дерева игры он фактически
находится. Этому игроку известно лишь некоторое множество позиций, включающее
в себя его фактическую позицию. Такое множество позиций называется информационным множеством.
Таким образом, в игре с неполной информацией игрок при своем ходе знает, в каком информационном множестве он находится, но ему неизвестно, в какой именно позиции этого множества.
Позиции, принадлежащие одному и тому же информационному множеству, объединяются пунктирными линиями.
Рассмотрим примеры двух игр, состоящих из двух ходов, которые последовательно делают участвующие в ней игроки А и В. Начинает игрок А: он выбирает одну из двух возможных альтернатив — число х, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива). На ход игрока А игрок В отвечает своим ходом, выбирая одну из двух возможных альтернатив — число у, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива).
И в результате игрок А получает вознаграждение или вынужден платить штраф.
Пример 13.
1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.
2-й ход. Игрок В выбирает число у из множества двух чисел {1,2}, зная выбор числа х игроком А.
Функция W(x, у) выплат игроку А за счет игрока В задается так
W(l, l) = 1, W(2, l) = -2,
W(l, 2) = -l, W(2, 2)= 2.
На рис. 3 показаны дерево игры и информационные множества.
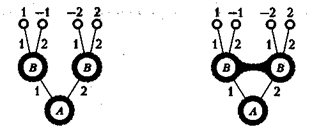
Рис. 3 Рис.4
Пример 14. В случав, вели выполнены все условия предыдущего примера, кроме одного — хода игрока В.
2-й ход — игрок В выбирает число у из множества двух чисел {1, 2}, не зная выбора числа х игроком А, информационные множества выглядят так, как показано на рис. 4.
2. Нормализация позиционной игры
Заранее определенную последовательность ходов игрока, выбранную им в зависимости от информации о ходах другого игрока и ходах игрока О (природы), будем называть чистой стратегией этого игрока.
В том случае, если в игре нет случайных ходов (игрок О в игре не участвует), выбор игроком А и игроком В чистых стратегий однозначно определяет исход игры — приводит к окончательной позиции, где игрок А. и получает свой выигрыш. Это обстоятельство позволяет сводить позиционную игру к матричной игре.
Процесс сведения позиционной игры к матричной называется нормализацией позиционной игры.
Покажем на нескольких примерах, как это делается.
Пример 13 (продолжение). Опишем стратегии игроков.
Стратегию игрока А можно задать одним числом х, показывающим, какую альтернативу, первую или вторую, выбрал игрок.
Тем самым, у игрока А две чистых стратегии:
А1 —выбрать х = 1, А2 — выбрать х = 2.
Стратегию игрока В, принимая во внимание, что выбор игрока А на 1-м ходе ему известен, удобно описывать упорядоченной парой
[y1, y2].
Здесь y1 (y1 = 1, 2) — альтернатива, выбираемая игроком В при условии, что игрок А выбрал первую альтернативу, х = 1, a y2 (y2 = 1, 2) — альтернатива, выбираемая игроком В при условии, что игрок А выбрал вторую альтернативу, х = 2.
Например, выбор игроком В стратегии [2, 1] означает, что если на 1-м ходе игрок А выбрал х = 1, то игрок В на своем ходе должен выбрать у = 2. Если же на 1-м xoде игрок А выбрал х = 2, то согласно этой стратегии игрок В на своем ходе должен выбрать у = 1.
Таким образом, у игрока В четыре чистых стратегии:
В1 — [1,1], у = 1 при любом выборе х;
В2 — [1, 2], у = х при любом выборе х;
В3 — [2,1], у ≠ х при любом выборе х;
В4 — [2, 2], у = 2 при любом выборе х.
Покажем теперь, как рассчитываются выигрыши игрока А в зависимости от примененных стратегий.
Пусть, например, игрок А выбрал стратегию А1 — (1), а игрок В — стратегию В2 — [1, 2]. Тогда х = 1, а из стратегии [1, 2] вытекает, что у = 1. Отсюда
W(х, y) = W(1, 1) = 1.
Остальные выигрыши рассчитываются совершенно аналогично.
Результаты расчетов записывается обычно или в виде таблицы выигрышей игрока А
| В1 | В2 | В3 | В4 | ||
| [1, 1] | [1, 2] | [2, 1] | [2, 2] | ||
| А1 | х = 1 | W(1, 1) | W(1, 1) | W(1, 2) | W(1, 2) |
| А2 | х = 2 | W(2, 1) | W(2, 2) | W(2, 1) | W(2, 2) |
или в вида матрицы игры
 ,
,
где, как обычно, строки соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В,
Полученная матрица имеет седловую точку. Оптимальные стратегии игроков: А1 — (1) и В3 — [2, 1]. Тем самым, игрок А на 1-м ходе выбирает х = 1, а игрок В на 2-м ходе выбирает у = 2. Цена игры v = -1.
Пример 14 (продолжение). Опишем стратегии игроков.
У игрока А они те же, что и в предыдущем примере
А1 – выбрать х = 1, А2 — выбрать х = 2.
Так как игроку В выбор игрока А неизвестен, то есть игрок В не знает, в какой именно из двух позиций он находится (см. рис. 4), то у него те же две стратегии:
В1 — выбрать у = 1, В2 — выбрать у = 2.
Соответствующие таблица выигрышей игрока А и матрица игры имеют следующий вид
| В1 | В2 | ||
| Y = 1 | y = 2 | ||
| А1 | х = 1 | W(1, 1) | W(1, 2) |
| А2 | х = 2 | W(2, 1) | W(2, 2) |

Полученная матрица седловой точки не имеет. Оптимальные смешанные стратегии игроков: Р = {2/3, 1/3} и Q = {1/2, 1/2}. Цена игры v = 0.
Замечание 1. На этих двух примерах хорошо видно, что результат сведения позиционной игры к матричной напрямую зависит от степени информированности игроков. В частности, отсутствие у игрока В сведений о выборе, сделанном игроком А приводит к уменьшению количества его возможных стратегий. Сравнивая, ответы, полученные в примерах 13 и 14, замечаем, что, снижение уровня информированности игрока (в данном случае — игрока В) делает для него исход игры менее, благоприятными.
Замечание 2. Приведенные выше примеры не исчерпывают всех возможных вариантов даже в этом, самом простом, случае двухходовых позиционных игр.
Рассмотрим теперь несколько примеров сведения к матричным играм позиционных игр, состоящих из трех ходов, сосредоточив при этом основное внимание на одном из наиболее ответственных шагов нормализации — описании стратегий игроков.
Пример 15.
1-й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}.
2-й ход делает игрок В: зная выбранное игроком А число х, он выбирает число у из множества двух чисел {1, 2}.
3-й ход делает игрок А: не зная о выбранном игроке В числе у на 2-м ходе и забыв выбранное им самим на 1-м ходе число х, он выбирает число z из множества двух чисел {1, 2}.
После этого игрок А получает вознаграждение W(x, у, z) за счет игрока В, например, такое:
W(1, 1, 1) = -2 W(2, 1, 1) = 3
W(1, 1, 2) = 4 W(2, 1, 2) = 0
W(1, 2, 1) = 1 W(2, 2, 1) = -3
W(1, 2, 2) = -4 W(2, 2, 2) = 5
На рис.5 показаны дерево игры и информационные множества.

Рис. 5
Нормализуем эту игру.
Поскольку игроку В выбор игрока А на 1-м ходе известен, то у игрока В те же четыре стратегии, что и в примере 13:
В1 – [1, 1], В2 – [1, 2], В3 – [2, 1], В4 – [2, 2].
Игрок А на 3-м ходе не знает предыдущих выборов — ни значения х, ни значения у. Поэтому каждая его стратегия состоит просто из пары чисел (х, z), где x (х = 1, 2) — альтернатива, выбираемая игроком А на 1-м ходе, а z (z = 1, 2) — альтернатива, выбираемая игроком А на 3-м ходе.
Например, выбор игроком А стратегии (2, 1) означает, что на 1-м ходе он выбирает x = 2, а на 3-м ходе — z = 1.
Таким образом, у игрока А четыре стратегии:
A1 – [1, 1], A2 – [1, 2], A3 – [2, 1], A4 – [2, 2].
Покажем теперь, как рассчитываются выигрыши игрока А в зависимости от стратегий, применяемых в данной игре. Пусть, например, игрок А выбрал стратегию A2 — (1, 2), а игрок В — стратегию В3 — (2, 1]• Тогда х = 1, откуда вытекает, что у = 2. Значение z = 2 выбрано игроком А независимо от выбора игрока В. Вычисляя значение функции выигрышей для этого набора, получаем
W(x, y, z) = W(1, 2, 2) = -4.
В результате подобных рассуждений получаются и остальные пятнадцать выигрышей. Это позволяет построить таблицу выигрышей игрока А. Имеем
| В1 | В2 | В3 | В4 | ||
| [1, 1] | [1, 2] | [2, 1] | [2, 2] | ||
| А1 | (1, 1) | W(1, 1, 1) | W(1, 1, 1) | W(1, 2, 1) | W(1, 2, 1) |
| А2 | (1, 2) | W(1, 1, 2) | W(1, 1, 2) | W(1, 2, 2) | W(1, 2, 2) |
| А3 | (2, 1) | W(2, 1, 1) | W(2, 2, 1) | W(2, 1, 1) | W(2, 2, 1) |
| А4 | (2, 2) | W(2, 1, 2) | W(2, 2, 2) | W(2, 1, 2) | W(2, 2, 2) |
или
 .
.
Пример 16.
1-й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}.
2-й ход делает игрок В: не зная о выборе игрока А на 1-м ходе, он выбирает число у из множества двух чисел {1, 2}.
3-й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, не зная ни значения х, ни значения у.
После этого игроки расплачиваются по правилу, указанному в примере 15.
Графическое представление этой игры показано на рис. 6.

Рис. 6
Ясно, что у игрока А те же четыре стратегии, что и в примере 15:
A1 – [1, 1], A2 – [1, 2], A3 – [2, 1], A4 – [2, 2].
У игрока В всего две стратегии:
B1 – выбрать y = 1, B2 – выбрать y = 2
В этом случае (весьма слабой информированности игроков) таблица выигрышей игрока A и соответствующая матрица строятся совсем просто. Имеем
| В1 | В2 | ||
| y = 1 | y = 2 | ||
| А1 | (1, 1) | W(1, 1, 1) | W(1, 1, 1) |
| А2 | (1, 2) | W(1, 1, 2) | W(1, 2, 2) |
| А3 | (2, 1) | W(2, 1, 1) | W(2, 2, 1) |
| А4 | (2, 2) | W(2, 1, 2) | W(2, 2, 2) |

Оптимальные смешанные стратегии игроков и цена игры соответственно равны:

В следующем примере информационные множества выглядят немного иначе.
Пример 17.
1-й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}.
2-й ход делает игрок В: не зная о выборе игрока А на 1-м ходе, он выбирает число у из множества двух чисел {1, 2}.
3-й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, зная выбор у игрока В на 2-м ходе, но не помня собственного выбора х на 1-м ходе.
После этого игроки расплачиваются по правилу, указанному в примере 15.
Графическое представление этой игры показано на рис. 7.

Рис. 7
Поскольку игроку В неизвестен выбор игрока А на 1-м ходе, то, выполняя свой ход, он не знает, в какой именно из двух возможных позиций он находится. Поэтому у игрока В всего две стратегии:
B1 – выбрать y = 1, B2 – выбрать y = 2
При описании стратегий игрока А нужно исходит из того, что к 3-му ходу игрок А утратил сведения о собственном выборе на 1-м ходе, но ему известен выбор игрока В на 2-м ходе. Поэтому выбор числа z игроку А следует связать с известным ему к 3-му xоду значением у. Удобнее всего это сделать по аналогии с расчетом стратегий игрока В в примерах 13 и 15, т. е. при помощи упорядоченной пары
[z1, z2]
Здесь z1 (z1 = 1, 2) — альтернатива, выбираемая игроком А при условии, что игрок В выбрал первую альтернативу, у = 1, a z2 (z2 — 1, 2) — альтернатива, выбираемая игроком А при условии, что игрок В выбрал вторую альтернативу, у = 2.
Чистую стратегию игрока А в данной игре можно записать так
(x, [z1, z2]).
Здесь х (х = 1, 2) — альтернатива, которую игрок А выбирает на 1-м ходе, z1 (z1 = 1, 2) — альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал выбрал первую альтернативу (у = 1) и z2 (z2 — 1, 2) — альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал вторую альтернативу (у = 2).
Например, выбор игроком А стратегии (2, [2, 1]) означает, что на 1-м ходе игрок А выбирает x = 2, а на 3-м z = 2, если игрок В выбрал у = 1, и z = 1, если игрок В выбрал у = 2.
Тем самым, у игрока А восемь чистых стратегий:
A1 — (1, [1, 1]), A2 — (1, [1, 2]), A3 — (1, [2, 1]), A4 — (1, [2, 2]),
A5 — (2, [1, 1]), A6 — (2, [1, 2]), A7 — (2, [2, 1]), A8 — (2, [2, 2]),
Покажем теперь, как в зависимости от применяемых стратегий определяются элементы таблицы выигрышей игрока А.
Пусть, например, игрок А выбрал стратегию A3 — (1, [2, 1]), а игрок В — стратегию В2 — (2). Тогда x = 1, у = 2, а из [2, 1] вытекает, что z = 1. Отсюда
W(x, y, z) = W(1, 2, 1) = 1.
По этой же схеме вычисляются и остальные элементы таблицы.
В результате получаем
| В1 | В2 | |||
| (1) | (2) | |||
| А1 | (1, [1, 1]) | W(1, 1, 1) | W(1, 2, 1) | |
| А2 | (1, [1, 2]) | W(1, 1, 1) | W(1, 2, 2) | |
| А3 | (1, [2, 1]) | W(1, 1, 2) | W(1, 2, 1) | |
| А4 | (1, [2, 2]) | W(1, 1, 2) | W(1, 2, 2) | |
| А5 | (2, [1, 1]) | W(2, 1, 1) | W(2, 2, 1) | |
| А6 | (2, [1, 2]) | W(2, 1, 1) | W(2, 2, 2) | |
| А7 | (2, [2, 1]) | W(2, 1, 2) | W(2, 2, 1) | |
| А8 | (2, [2, 2]) | W(2, 1, 2) | W(2, 2, 2) | |

Оптимальные смешанны* стратегии игроков и цена игры соответственно равны:

Рассмотрим позиционную игру со случайным ходом.
Пример 18.
1-й ход производится случайно: игрок О выбирает число х, равное 1, с вероятностью 0,5 и равное 2 с такой же вероятностью.
2-й ход делает игрок А: он выбирает число у из множества двух чисел {1, 2}, не зная результатов случайного выбора на 1-м ходе.
3-й ход делает игрок В: он выбирает число z из множества двух чисел {1, 2}, зная о том, какое именно число х случайно выбрано игроком О на 1-м ходе и не зная выбора у игрока А на 2-м ходе.
После этого игроки расплачиваются, используя функцию W(x, y, z), ту же. что и в предыдущих примерах.
Графическое представление этой игры показано на рис.8.

Рис. 8
Опишем стратегии игроков
Поскольку игроку А исход случайного испытания неизвестен, то он имеет всего две стратегии:
А1 – (1), А2 – (2),
При построении своих стратегий игроку В естественно воспользоваться имеющейся у него информацией о результате 1-го хода. Это позволит ему описать свою стратегию упорядоченной парой
[z1, z2].
Здесь z1 (z1 = 1, 2) — альтернатива, выбираемая игроком В при условии, что х = 1, a z2 (z2 = 1, 2) — альтернатива, выбираемая игроком В при условии, что х = 2. Тем самым, у игрока В четыре стратегии:
В1 — [1, 1], В2 — [1, 2], В3 — [2, 1], В4 — [2, 2].
Покажем теперь, как определяются элементы таблицы выигрышей игрока А.
Пусть, например, игрок А выбрал стратегию А1 — (1), а игрок В — стратегию В3 — [2, 1].
Различаются два случая
1) х = 1 и 2) х = 2.
Если х = 1, то стратегия В3 указывает игроку В3 его Выборг z = 2. А так как у = 1, то в результате имеем
W(x, y, z) = W(1, 1, 2) = 4.
Если х = 2, то стратегия В3 указывает игроку В его выбор z = 1. А так как у = 1, то в результате
W(x, y, z) = W(2, 1, 1) = 3.
Поскольку первая и вторая альтернативы на 1-м ходе выбираются с вероятностями 0,5 и 0,5, то и вышеуказанные выигрыши появляются с теми же вероятностями и, следовательно, средний выигрыш игрока А при этих стратегиях определяется так
4 x 0,5 + 3 x 0,5 = 3,5.
Аналогичным образом рассчитывая остальные средние выигрыши, получаем при х = 1
| В1 | В2 | В3 | В4 | ||
| [1, 1] | [1, 2] | [2, 1] | [2, 2] | ||
| А1 | (1) | W(1, 1, 1) | W(1, 1, 1) | W(1, 1, 2) | W(1, 1, 2) |
| А2 | (2) | W(1, 2, 1) | W(1, 2, 1) | W(1, 2, 2) | W(1, 2, 2) |
или
 ,
,
при х = 2
| В1 | В2 | В3 | В4 | ||
| [1, 1] | [1, 2] | [2, 1] | [2, 2] | ||
| А1 | (1) | W(2, 1, 1) | W(2, 1, 1) | W(2, 1, 2) | W(2, 1, 2) |
| А2 | (2) | W(2, 2, 1) | W(2, 2, 2) | W(2, 2, 2) | W(2, 1, 1) |
или
 .
.
Искомая матрица игры имеет следующий вид
 .
.
Наконец, рассмотрим пример позиционной игры со случайным разыгрыванием права первого хода.
Пример 19.
1-й ход делает игрок О, выбирая число х, равное 1 с вероятностью 2/3 и равное 2 с вероятностью 1/3.
Если х = 1, то на 2-м ходе игрок А выбирает число у из множества двух чисел {1, 2}, зная результат случайного выбора на 1-м ходе, а на 3-й ходе игрок В выбирает число z из множества двух чисел {1, 2}, зная х, но не зная у.
Если x = 2, то на 2-м ходе игрок В выбирает число у из множества двух чисел {1, 2}, зная результат случайного выбора на 1-м ходе, а на 3-м ходе игрок А выбирает число z из множества двух чисел {1, 2}, зная х, но не зная у.
После этого игроки расплачиваются, используя функцию W(x, y, z), ту же, что и в предыдущих примерах.
Графическое представление этой игры показано на рис. 9.

Рис. 9
Чистую стратегию игрока А в данной игре можно описать упорядоченной парой

где у (у = 1, 2) — выбор игрока А на 2-м ходе, если на 1-м ходе выбрано х = 1, а z (z = 1, 2) — выбор игрока А на 3-м ходе, если на 1-м ходе выбрано х = 2.
Например, стратегия |1, 2| означает, что на 2-м хода игрок А выбирает у = 1, а на 3-м ходе — z = 2.
Тем самым, у игрока А четыре стратегии:
А1 — |1, 1|, А 2 — |1, 2|, А 3 — |2, 1|, А 4 — |2, 2|.
У игрока В те же четыре стратегии:
В1 — |1, 1|, В2 — |1, 2|, В3 — |2, 1|, В4 — |2, 2|.
Покажем теперь, как находятся элементы матрицы выигрышей игрока А.
Пусть, например, игрок А применяет стратегию А2 — |1, 2|, а игрок В — стратегию В3 — |2, 1|.
Различаются два случая
1) х = 1 и 2) х = 2.
По условию при х = 1 игрок А имеет возможность сделать только 2-й ход (выбрать у), а игрок В — только 3-й (выбрать 2). При х = 2 их возможности меняются местами: игроку В предоставлено право 2-го хода (выбрать у), а игроку А — 3-го (выбрать z). .
Если х = 1, то стратегия А2 указывает игроку А при 2-м ходе взять у = 1, а стратегия В3 указывает игроку В при 3-м ходе взять z = 1. В результате
W(x, y, z) = W(1, 1, 1) = -2.
Если х = 2, то стратегия B3 указывает игроку В при 2-м ходе взять у = 2, а стратегия А2 указывает игроку А при 3-м ходе взять z = 2. В результате
W(x, y, z) = W(2, 2, 2) = 5.
Поскольку первая и вторая альтернативы на 1-м ходе выбираются соответственно с вероятностями 2/3 и 1/3, то и найденные выигрыши появляются с теми же вероятностями. Следовательно, математическое ожидание выигрыша игрока А при таких стратегиях рассчитывается так
 .
.
Итак,
при х = 1
| В1 | В2 | В3 | В4 | ||
| |1, 1| | |1, 2| | |2, 1| | |2, 2| | ||
| А1 | |1, 1| | W(1, 1, 1) | W(1, 1, 2) | W(1, 1, 1) | W(1, 1, 2) |
| А2 | |1, 2| | W(1, 1, 1) | W(1, 1, 2) | W(1, 1, 1) | W(1, 1, 2) |
| А3 | |2, 1| | W(1, 2, 1) | W(1, 2, 2) | W(1, 2, 1) | W(1, 2, 2) |
| А4 | |2, 2| | W(1, 2, 1) | W(1, 2, 2) | W(1, 2, 1) | W(1, 2, 2) |
или
 ,
,
при х = 2
| В1 | В2 | В3 | В4 | ||
| |1, 1| | |1, 2| | |2, 1| | |2, 2| | ||
| А1 | |1, 1| | W(2, 1, 1) | W(2, 1, 1) | W(2, 2, 1) | W(2, 2, 1) |
| А2 | |1, 2| | W(2, 1, 2) | W(2, 1, 2) | W(2, 2, 2) | W(2, 2, 2) |
| А3 | |2, 1| | W(2, 1, 1) | W(2, 1, 1) | W(2, 2, 1) | W(2, 2, 1) |
| А4 | |2, 2| | W(2, 1, 2) | W(2, 1, 2) | W(2, 2, 2) | W(2, 2, 2) |
или
 .
.
Отсюда получаем искомую матрицу игры
 .
.
Замечание. Графическое представление и функция выигрышей полностью определяют позиционную игру. В рассмотренных выше примерах 16-19 мы пользовались одной и той же функцией и одним и тем же деревом. Отличие было только в маркировке вершин дерева и информационных множествах. При построении последних необходимо соблюдать два правила:
1) в одно информационное множество могут входить позиции только одного игрока,
2) цепь, определяющая партию игры, может иметь с информационным множеством не более одной общей позиции.

Рис. 10
Как показывает рис. 10, и при таких ограничениях информационные множества могут выглядеть довольно необычно.
3. Позиционные игры с полной информацией
Позиционная игра называется игрой с полной информацией, если в каждой позиции любой ее партии игрок, делающий ход, знает, какие альтернативы были выбраны на предыдущих ходах. В графическом описании каждая вершина дерева такой игры представляет собой отдельное информационное множество.
Примерами позиционных игр с полной информацией могут служить крестики-нолики, шашки и шахматы.
Основная особенность позиционной игры с полной информацией состоит в том, что соответствующая ей матрица выигрышей всегда имеет седловую точку, то есть в игре с полной информацией существуют оптимальные чистые стратегии и, значит, равновесная ситуация.
Сказанное означает, что в шахматах (крестиках-ноликах, шашках) уже в начальной позиции либо имеется способ выигрыша за белых, либо способ выигрыша за черных, либо как та, так и другая сторона способна форсировать ничью.
Однако известное доказательство существования равновесной ситуации неконструктивно и не дает эффективных приемов фактического нахождения решения игры.
И такие способы (стратегии) в шахматах не найдены до сих пор, и даже неизвестно, какая из перечисленных возможностей имеет место на самом деле.
Иное дело с игрой крестики-нолики: стратегий в ней немного и она разобрана до самого конца — существуют оптимальные чистые стратегии, ведущие игроков к ничьей.
Рассмотрим несколько примеров.
1. Как нетрудно заметить, двухходовая игра из примера 11 является игрой с полной информацией. Ее нормализация приводит к матрице с седловой точкой (см. пример 13).
2. «Выкладывание монет на стол» . Два игрока поочередно кладут монеты одинаковых размеров на обыкновенный стол, всякий раз выбирая произвольное доступное место для монеты (взаимное накрывание монет не допускается). Тот из игроков, кто положит монету, не оставляющую места для новых монет, выигрывает.
Это игра с полной информацией. Существует вполне определенная стратегия, обеспечивающая выигрыш тому из игроков, кто начинает игру. А именно, начинающий игру должен положить первую монету точно в центр стола и на каждый ход противника отвечать симметричным ходом. Исход игры от стратегии второго игрока не зависит.
3. «Переговоры» . В переговорах участвуют две стороны А и В. В слегка идеализированном варианте это может выглядеть, например, так.
Сначала сторона А высказывает одно из нескольких предложений, способных заинтересовать сторону В. Затем сторона В, ознакомившись с предложением стороны А, высказывает одно из нескольких встречных предложений, способных, по ее мнению, заинтересовать сторону А. В свою очередь, сторона А, ознакомившись с реакцией стороны В на сделанные предложения, высказывает ей новое предложение, внеся одну из нескольких возможных корректировок в свое первоначальное предложение с учетом мнения стороны В и т.д.
Если предмет переговоров сложен, то подобный обмен ходов может затянуться. Однако любые переговоры непременно заканчиваются. И там, на финише, ждет функция выигрышей.
Попробуем смоделировать короткий переговорный процесс трехходовой позиционной игрой.
Предположим, что переговоры заканчиваются через три хода, на каждом из которых соответствующая сторона имеет возможность выбора из двух альтернатив, и опишем соответствующую позиционную игру.
1-й ход делает сторона А: она выбирает одно из двух возможных предложений — число х из множества двух чисел {1, 2}.
2-й ход делает сторона В: она выбирает число у из множества двух чисел {1, 2}, зная число х, предложенное стороной А.
3-й ход делает сторона А: она выбирает число z из множества двух чисел {1, 2}, зная о предложении стороны В на 2-м ходе и помня собственное предложение на 1-м ходе.

Рис. 11
После этого сторона А либо получает вознаграждение (например, в виде кредита от стороны В), либо выплачивает стороне В штраф.
Все эти возможности описываются функцией выигрышей W(x, у, z), заданной следующей таблицей
W(1, 1, 1) = a W(2, 1, 1) = e
W(1, 1, 2) = b W(2, 1, 2) = f
W(1, 2, 1) = c W(2, 2, 1) = g
W(1, 2, 2) = d W(2, 2, 2) = h.
Графическое представление этой игры показано на рис. 11.
Ясно, что описанная позиционная игра является игрой с полной информацией.
Начнем с описания возможных стратегий игрока В.
Поскольку игроку В выбор игрока А на 1-м ходе известен, то у игрока В те же четыре стратегии, что и в примере 13:
В1 – [1, 1], В2 – [1, 2], В3 – [2, 1], В4 – [2, 2],
С описания возможных стратегий игрока А дело обстоит немного посложнее — их восемь.
Чистая стратегия игрока А в данной игре описывается упорядоченной тройкой
(x, [z1, z2]).
Здесь x (x = 1, 2) — альтернатива, которую игрок А выбирает на 1-м ходе, z1 (z1 = 1, 2)— альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал первую альтернативу (у = 1) и z2 (z2 = 1, 2) — альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал вторую альтернативу (у = 2).
Например, выбор игроком А стратегии (1, (2, 1]) означает, что на 1-м ходе игрок А выбирает х = 1, а на 3-м z = 2. если игрок В выбрал у = 1, и z = 1, если игрок В выбрал у = 2.
Тем самым, у игрока А восемь чистых стратегий:
A1 — (1, [1, 1]), A2 — (1, [1, 2]), A3 — (1, [2, 1]), A4 — (1, [2, 2]),
A5 — (2, [1, 1]), A6 — (2, [1, 2]), A7 — (2, [2, 1]), A8 — (2, [2, 2]),
Покажем теперь, как в зависимости от применяемых стратегий определяются элементы таблицы выигрышей игрока А.
Пусть, например, игрок А выбрал стратегию A6 — (2, [1, 2]), а игрок В — стратегию В3 – [2, 1]. Тогда х = 2. Из [2, 1] вытекает, что у = 1, а из (2, [1, 2]), что z = 1. Отсюда
W(x, y, z) = W(2, l, 1) = е.
Рассчитывая по этой же схеме все остальные элементы таблицы выигрышей, в итоге получим
| В1 | В2 | В3 | В4 | ||
| [1, 1] | [1, 2] | [2, 1] | [2, 2] | ||
| А1 | (1, [1, 1]) | W(1, 1, 1) | W(1, 1, 1) | W(1, 2, 1) | W(1, 2, 1) |
| А2 | (1, [1, 2]) | W(1, 1, 1) | W(1, 1, 1) | W(1, 2, 2) | W(1, 2, 2) |
| А3 | (1, [2, 1]) | W(1, 1, 2) | W(1, 1, 2) | W(1, 2, 1) | W(1, 2, 1) |
| А4 | (1, [2, 2]) | W(1, 1, 2) | W(1, 1, 2) | W(1, 2, 2) | W(1, 2, 2) |
| А5 | (2, [1, 1]) | W(2, 1, 1) | W(2, 2, 1) | W(2, 1, 1) | W(2, 2, 1) |
| А6 | (2, [1, 2]) | W(2, 1, 1) | W(2, 2, 2) | W(2, 1, 1) | W(2, 2, 2) |
| А7 | (2, [2, 1]) | W(2, 1, 2) | W(2, 2, 1) | W(2, 1, 2) | W(2, 2, 1) |
| А8 | (2, [2, 2]) | W(2, 1, 2) | W(2, 2, 2) | W(2, 1, 2) | W(2, 2, 2) |

Вследствие того, что рассматриваемая позиционная игра является игрой с полной информацией, полученная матрица имеет седловую точку при любой функции выигрышей. В атом легко убедиться, произвольно выбирая значат» параметров а, b, c, d, е, f, g и h.
При увеличении числа ходов стратегии в позиционной игре с полной информацией строятся по аналогичной схеме.
Рассмотрим, например, четырехходовую позиционную игру.
1-й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}.
2-й ход делает игрок В: он выбирает число у из множества двух чисел {1, 2}, зная число х, выбранное игроком А на 1-м ходе.
3-й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, зная число у, выбранное игроком В на 2-м ходе, и помня свой выбор числа х на 1-м ходе.
4-й ход делает игрок В: он выбирает число u из множества двух чисел {1, 2}, зная число z, выбранное игроком А на 3-м хода, помня свой выбор числа у на 2-м хода и зная выбор игрока А на 1-м ходе — число х.
После этого игроки А и В расплачиваются а соответствии с заданной функцией выигрышей W(x, y, z, u).
В этой игре стратегии у игрока А те же, что и в задаче, рассмотренной выше: каждая из них задается тройкой вида
(x, [z1, z2]),
и общее их число равно восьми.
Что касается стратегий игрока В, то в этой игре их шестнадцать и каждая из них задается четверкой вида
([y1, y2], [u1, u2]).
Матрица выигрышей игрока А в данной игре имеет размер 8 х 16. Покажем, как определяются ее элементы в зависимости от применяемых стратегий игроков.
Пусть, например, игрок А выбрал стратегию А' — (2, [2, 1]), а игрок В стратегию В' — ([2, 1], [1,2]). Тогда х = 1, у = 2, а z = 1. Из того, что [u1, u2] = [1, 2], получаем, что u = 1. Отсюда следует, что искомый элемент матрицы выплат равен
W(1, 2, 1, 1)
Остальные элементы матрицы вычисляются аналогично.
Так как эта позиционная игра также является игрой с полной информацией, то получаемая матрица будет иметь седловую точку.
Несколько слов в заключение
В рассмотренных примерах основное внимание было; уделено описанию процесса нормализации позиционной игры — построению дерева игры и информационных множеств, выработке стратегий игроков и вычислению элементов платежной матрицы. Следующий естественный шаг — отыскание цены игры и оптимальных стратегий игроков — проводится методами, о которых рассказывалось в главе, посвященной матричным играм.
Мы достаточно подробно остановились на позиционных играх двух лиц, где был: явно выражены интересы одного из игроков (игрока А). Следует, однако, иметь в вид] что в одних случаях интересы игрока В могут быть полностью противоположным интересам игрока А, в то время как в других вполне может оказаться, что то, что хорошо для одного игрока, не обязательно плохо для другого. Приведем два простых примера.
Пример А.
1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.
2-й ход. Игрок В выбирает число у из множества двух чисел {1, 2}, зная выбор числа х игроком А.
Функции выплат игрокам А и В — WA(x, у) и WB(x, у) соответственно — задаются так:
WA (1, 1) = 1, WA (1, 2) = -1, WA (2, 1) = -2, WA (2, 2) = 2,
WB (1, 1) = 2, WB (1, 2)= 1, WB (2, 1) = 1, WB (2, 2) = 2.
Дерево игры показано на рис. 12. Исход игры зависит от того, каковы намерения игрока В — максимизировать свой выигрыш:
WB(x, у) → max,
или максимизировать свой относительный выигрыш:
WB(x, у) WA(x, у)- , у) → max.
В первом Случав это достигается так:
При x = 1 у = 1 и WB(1, 1) = 2 (WA (1, 1) = 1);
При x = 2 у = 2 и WB (2, 2) = 2 (WA (2, 2) = 2).
Во втором случае:
При x = 1 у = 2 и WB(1, 2) - WA (1, 2) = 1 – (-1) = 2);
При x = 2 у = 1 и WB (2, 1) - WA (2, 1) = 1 – (-2) = 3).
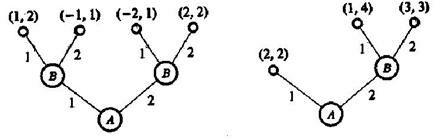
Рис.12 Рис. 13
Пример Б. Игра задается деревом (см. рис. 13).
1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.
Если х = 1, то каждый из игроков получает свой выигрыш, равный 2.
Если х = 2, то право 2-го хода получает игрок В, где он и выбирает число у из множества двух чисел {1, 2}.
При у = 1 выигрыш игрока А равен 1, а игрока В — 4. При у = 2 оба игрока получают поровну — по 3.
В случае, когда каждый из игроков стремится к получению максимального выигрыша и любые виды кооперации запрещены, исход игры ясен — игрок А выбирает х = 1, и игра заканчивается. Но при х =2 и у = 2 каждый из игроков получает по 3 (такой исход предпочтительнее простейшего (1, 1)), и, если допустить соглашение между игроками, это обстоятельство вполне может изменить исход игры.
3.6 Принятие решений и теория игр. Примеры.
В теории игр рассматриваются ситуации, связанные с принятием решений, в которых два разумных противника имеют конфликтующие цели. К числу типичных примеров относится рекламирование конкурирующих товаров и планирование военных стратегий противоборствующих армий. Эти ситуации принятия решений отличаются от рассмотренных ранее, где природа не рассматривается в роли недоброжелателя.
В игровом конфликте участвуют два противника, именуемые игроками, каждый из которых имеет некоторое множество (конечное или бесконечное) возможных выборов, которые называются стратегиями. С каждой парой стратегий связан платеж, который один из игроков выплачивает другому. Такие игры известны как игры двух лиц с нулевой суммой, так как выигрыш одного игрока равен проигрышу другого. В такой игре достаточно задать результаты в виде платежей для одного из игроков. При обозначении игроков через А и В с числом стратегий m и n соответственно, игру обычно представляют в виде матрицы платежей игроку А:
| B1 | B2 | … | Bn | |
| A1 | a11 | a12 | … | a1n |
| A2 | a21 | a22 | … | a2n |
| . . . | . . . | . . . | . . . | . . . |
| Am | am1 | am2 | … | amn |
Такое представление матричной игры означает, что если игрок А использует стратегию i, а игрок В — стратегию j, то платеж игроку А составляет аij и, следовательно, игроку В — – аij.
3.6.1. Оптимальное решение игры двух лиц с нулевой суммой
Поскольку игры берут свое начало в конфликте интересов, оптимальным решением игры является одна или несколько таких стратегий для каждого из игроков, при этом любое отклонение от данных стратегий не улучшает плату тому или другому игроку. Эти решения могут быть в виде единственной чистой стратегии или нескольких стратегий, которые являются смешанными в соответствии с заданными вероятностями. Рассматриваемые ниже примеры демонстрируют перечисленные случаи.
Пример 3.6-1
Две компании А и В продают два вида лекарств против гриппа; Компания А рекламирует продукцию на радио (A1), телевидении (А2) и в газетах (А3) – Компания В, в дополнение к использованию радио (B1), телевидения (В2) и газет (В3), рассылает также по почте брошюры (B4). В зависимости от умения и интенсивности проведения рекламной кампании, каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица характеризует процент клиентов, привлеченных или потерянных компанией А.
| B1 | B2 | B3 | B4 | Минимумы строк | |
| A1 | 8 | –2 | 9 | –3 | –3 |
| A2 | 6 | 5 | 6 | 8 | 5← Максимин |
| A3 | –2 | 4 | –9 | 5 | –9 |
| Максимумы столбцов | 8 | 5 | 9 | 8 | |
|
| Минимакс |
Решение игры основано на обеспечении наилучшего результата из наихудших для каждого игрока. Если компания А выбирает стратегию А1, то, независимо от того, что предпринимает компания В, наихудшим результатом является потеря компанией А 3% рынка в пользу компании В. Это определяется минимумом элементов первой строки матрицы платежей. Аналогично при выборе стратегии А2 наихудшим исходом для компании А является увеличение рынка на 5% за cчет компании В. Наконец, наихудшим исходом при выборе стратегии А3 является потеря компанией А 9% рынка в пользу компании В. Эти результаты содержатся в столбце "Минимумы строк". Чтобы достичь наилучшего результата из наихудших, компания А выбирает стратегию А2, так как она соответствует наибольшему элементу столбца "Минимумы строк".
Рассмотрим теперь стратегии компании В. Так как элементы матрицы являются платежами компании А, критерий наилучшего результата из наихудших для компании В соответствует выбору минимаксного значения. В результате приходим к выводу, что выбором компании В является стратегия В2.
Оптимальным решением игры является выбор стратегий А2 и В2, т.е. обеим компаниям следует проводить рекламу на телевидении. При этом выигрыш будет в пользу компании А, так как ее рынок увеличится на 5%. В этом случае говорят, что цена игры равна 5% и что компании А и В используют стратегии, соответствующие седловой точке.
Решение, соответствующее седловой точке, гарантирует, что ни одной компании нет смысла пытаться выбрать другую стратегию. Действительно, если компания В переходит к другой стратегий (Bl, B3 или В4), то компания А может сохранить свой выбор стратегии А2, что приведет к большей потере рынка компанией В (6% или 8%). По тем же причинам компании А нет резона использовать другую стратегию, ибо если она применит, например, стратегию А3, то компания В может использовать свою стратегию В3 и увеличить свой рынок на 9%. Аналогичные выводы имеют место, если компания А будет использовать стратегию А1.
Оптимальное решение игры, соответствующее седловой точке, не обязательными должно характеризоваться чистыми стратегиями. Вместо этого оптимальное решение может требовать смешивания случайным образом двух или более стратегий, как это сделано в следующем примере.
Пример 3.6-2
Два игрока А и В играют в игру, основанную на подбрасывании монеты. Игроки одновременно и независимо друг от друга выбирают герб (Г) или решку (Р). Если результаты двух подбрасываний монеты совпадают (т.е. ГГ или РР), то игрок А получает один доллар от игрока В. Иначе игрок А платит один доллар игроку В.
Следующая матрица платежей игроку А показывает величины минимальных элементов строк и максимальных элементов столбцов, соответствующих стратегиям обоих игроков.
Максиминная и минимаксная величины (цены) для этой игры равны – 1 доллар и 1 доллар соответственно. Так как эти величины не равны между собой, игра не имеет решения в чистых стратегиях; В частности, если игрок А использует стратегию АГ, игрок В выберет стратегию ВР, чтобы получить от игрока А один доллар. Если это случится, игрок А может перейти к стратегии АР, чтобы изменить исход игры и получить один доллар от игрока В. Постоянное искушение каждого игрока перейти к другой стратегии указывает на то, что решение в виде чистой стратегии неприемлемо. Вместо этого оба игрока должны использовать надлежащую случайную комбинацию своих стратегий. В рассматриваемом примере оптимальное значение цены игры находится где-то между максиминной и минимаксной ценами для этой игры:
максиминная (нижняя) цена ≤ цена игры ≤ минимаксная (верхняя) цена.
Следовательно, в данном случае цена игры должна лежать в интервале [–1,1], измеряемом в долларах.
Упражнения 3.6,а
1. Определите решение, определяемое седловой точкой, соответствующие чистые стратегии и цену игры для следующих игр, в которых платежи заданы для игрока А.
а)
| B1 | B2 | B3 | B4 | |
| A1 | 8 | 6 | 2 | 8 |
| A2 | 8 | 9 | 4 | 5 |
| A3 | 7 | 5 | 3 | 5 |
b)
| B1 | B2 | B3 | B4 | |
| A1 | 4 | –4 | –5 | 6 |
| A2 | –3 | –4 | –9 | –2 |
| A3 | 6 | 7 | –8 | –9 |
| A4 | 7 | 3 | –9 | 5 |
2. В следующих играх заданы платежи игроку А. Укажите область значений для параметров р и q, при которых пара (2, 2) будет седловой точкой в каждой игре.
а)
| B1 | B2 | B3 | |
| A1 | 1 | q | 6 |
| A2 | p | 5 | 10 |
| A3 | 6 | 2 | 3 |
b)
| B1 | B2 | B3 | |
| A1 | 2 | 4 | 5 |
| A2 | 10 | 7 | q |
| A3 | 4 | p | 6 |
3. Укажите область, которой принадлежит цена игры в каждом из следующих случаев, предполагая, что платежи заданы для игрока A.
а)
| B1 | B2 | B3 | B4 | |
| A1 | 1 | 9 | 6 | 0 |
| A2 | 2 | 3 | 8 | 4 |
| A3 | –5 | –2 | 10 | –3 |
| A4 | 7 | 4 | –2 | –5 |
b)
| B1 | B2 | B3 | B4 | |
| A1 | –1 | 9 | 6 | 8 |
| A2 | –2 | 10 | 4 | 6 |
| A3 | 5 | 3 | 0 | 7 |
| A4 | 7 | –2 | 8 | 4 |
c)
| B1 | B2 | B3 | |
| A1 | 3 | 6 | 1 |
| A2 | 5 | 2 | 3 |
| A3 | 4 | 2 | –5 |
d)
| B1 | B2 | B3 | B4 | |
| A1 | 3 | 7 | 1 | 3 |
| A2 | 4 | 8 | 0 | –6 |
| A3 | 6 | –9 | –2 | 4 |
4. Две фирмы производят два конкурирующих товара. Каждый товар в настоящее время контролирует 50% рынка. Улучшив качество товаров, обе фирмы собираются развернуть рекламные кампании. Если они не будут этого делать, то существующее состояние рынка не изменится. Однако если какая-либо фирма будет более активно рекламировать свои товары, то другая фирма потеряет соответствующий процент своих потребителей. Исследование рынка показывает, что 50% потенциальных потребителей получают информацию посредством телевидения 30% – через газеты и 20% – посредством радио.
а) Сформулируйте задачу в виде игры двух лиц с нулевой суммой и выберите подходящие средства рекламы для каждой фирмы.
b) Укажите интервал значений, которому принадлежит цена игры. Может ли каждая фирма действовать с единственной чистой стратегией?
5. Пусть aij – (i, j)-й элемент платежной матрицы с m стратегиями игрока A и n стратегиями игрока В. Элементы платежной матрицы представляют собой платежи игроку А. Докажите, что
 .
.
3.6.2. Решение матричных игр в смешанных стратегиях
Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Графический метод применим для решения игр, в которых хоть один игрок имеет две чистые стратегии. Этот метод интересен в том плане, что графически объясняет понятие седловой точки. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.
ГРАФИЧЕСКОЕ РЕШЕНИЕ ИГР. Рассмотрим игру 2 x n, в которой игрок А имеет две стратегии.
Игра предполагает, что игрок А смешивает стратегии А1 и А2 с соответствующими вероятностями x1 и 1 –х1, 0 ≤ x1 ≤ 1. Игрок В смешивает стратегии В1, В2,..., Вn с вероятностями у1, у2, ...,уп, где yj ≥ 0,j = 1, 2,..., и, y1 + у2 + …+ уn = 1. В этом случае ожидаемый выигрыш игрока А, соответствующий j-й чистой стратегии игрока В, вычисляется в виде
Следовательно, игрок А ищет величину х1, которая максимизирует минимум ожидаемых выигрышей
 .
.
Пример 3.6-3
Рассмотрим следующую игру 2x4, в которой платежи выплачиваются игроку А.
| B1 | B2 | B3 | B4 | |
| A1 | 2 | 2 | 3 | –1 |
| A2 | 4 | 3 | 2 | 6 |
Игра не .имеет решения в чистых стратегиях, и, следовательно, стратегии должны быть смешанными. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, приведены в следующей таблице.
| Чистые стратегии игрока В | Ожидаемые выигрыши игрока А |
| 1 | –2x1 + 4 |
| 2 | –x1 + 3 |
| 3 | x1 + 2 |
| 4 | –7x1 + 6 |
На рис. 14.6 изображены четыре прямые линии, соответствующие чистым стратегиям игрока В. Чтобы определить наилучший результат из наихудших, построения нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выигрыш для игрока А независимо от того, что делает игрок В. Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точке х1* = 0.5. Эта точка определяется пересечением прямых 3 и 4. Следовательно, оптимальным решением для игрока А является смешивание стратегий A1 и A2 вероятностями 0.5 и 0.5 соответственно. Соответствующая цена игры v определяется подстановкой х1 = 0.5 уравнение либо прямой 3, либо 4, что приводит к следующему.


рис. 14.6
Оптимальная смешанная стратегия игрока В определяется двумя стратегиями, которые определяют нижнюю огибающую графика. Это значит, что игрок В может смешивать стратегии B3 и В4, в этом случае у1 = y2 = 0 и у4 = 1 – у3. Следовательно, ожидаемые платежи игрока В, соответствующие чистым стратегиям игрока А, имеют следующий вид.
| Чистые стратегии игрока В | Ожидаемые выигрыши игрока А |
| 1 | 4ό3 – 1 |
| 2 | –4ò3 + 6 |
Наилучшее решение из наихудших для игрока В представляет собой точку минимума верхней огибающей заданных двух прямых (построение прямых и определение верхней огибающей будет для Вас поучительным). Эта процедура эквивалентна решению уравнения
 .
.
Его решением будет у3 = 7/8, что определяет цену игры v = 4 х (7/8) – 1 = 5/2.
Таким образом, решением игры для игрока А является смешивание стратегий А1 и А2 равными вероятностями 0.5 и 0.5, а для игрока В – смешивание стратегий В3 и В4 с вероятностями 7/8 и 1/8. (В действительности игра имеет альтернативное решение для игрока В, так как максиминная точка на рис. 14.6 определяется более чем двумя прямыми. Любая выпуклая линейная комбинация этих альтернативных решений также является решением задачи.)
Для игры, в которой игрок А имеет m стратегий, а игрок В – только две, решение находится аналогично. Главное отличие состоит в том, что здесь строятся графики функций, представляющих ожидаемые платежи второго игрока, соответствующие чистым стратегиям игрока А. В результате ведется поиск минимаксной точки верхней огибающей построенных прямых.
Упражнения 3.6,b
1. Решите графически игру с подбрасыванием монет из примера 3.6-2.
2. Робин часто путешествует между двумя городами. При этом есть возможность выбирать один из двух маршрутов: маршрут А представляет собой скоростное шоссе в четыре полосы, маршрут В – длинную обдуваемую ветром дорогу. Патрулирование дорог осуществляется ограниченным числом полицейских. Если все полицейские расположены на одном маршруте, Робин с ее страстным желанием ездить очень быстро, несомненно, получит штраф в 100 долларов за превышение скорости. Если полицейские патрулируют на двух маршрутах в соотношении 50 на 50, то имеется 50%-ная вероятность, что Робин получит штраф в 100 долларов на маршруте А и 30%-ная вероятность, что она получит такой же штраф на маршруте В. Кроме того, маршрут В длиннее, поэтому бензина расходуется на 15 долларов больше, чем на маршруте А. Определите стратегию как для Робин, так и для полиции.
3. Решите графически следующие игры, в которых платежи выплачиваются игроку А.
а)
| B1 | B2 | B3 | |
| A1 | 1 | –3 | 7 |
| A2 | 2 | 4 | –6 |
b)
| B1 | B2 | |
| A1 | 5 | 8 |
| A2 | 6 | 5 |
| A3 | 5 | 7 |
4. Дана следующая игра двух лиц с нулевой суммой.
| B1 | B2 | B3 | |
| A1 | 5.0 | 50.0 | 50.0 |
| A2 | 1.0 | 1.0 | 0.1 |
| A3 | 10.0 | 1.0 | 10.0 |
a) Проверьте, что смешанные стратегии с вероятностями (1/6, 0, 5/6) для игрока А и с вероятностями (49/54, 5/54, 0) для игрока В являются оптимальными, и определите цену игры.
b) Покажите, что цена игры равна
 .
.
решение матричных игр методами линейного программирования. Теория игр находится в тесной связи с линейным программированием, так как любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования и наоборот. Дж. Данциг [2] отмечает, что когда в 1947 году создатель теории игр Дж. фон Нейман впервые ознакомился с симплекс-методом, он сразу установил эта взаимосвязь и обратил особое внимание на концепцию двойственности в линейном программировании. Этот раздел иллюстрирует решение матричных игр методами линейного программирования.
Оптимальные значения вероятностей хi, i = 1, 2,..., m, игрока А могут быть определены путем решения следующей максиминной задачи.
 ,
,

Чтобы сформулировать эту задачу в виде задачи линейного программирования, положим
 .
.
Отсюда вытекает, что
 .
.
Следовательно, задача игрока А может быть записана в виде
Максимизировать z = v
при ограничениях
 ,
,

Отметим последнее условие, что цена игры v может быть как положительной, так и отрицательной.
Оптимальные стратегии у1, у2, ...,уn игрока В определяются путем решения задачи


Используя процедуру, аналогичную приведенной выше для игрока А, приходим к выводу, что задача для игрока В сводится к следующему.
Минимизировать w = v
при ограничениях


Две полученные задачи оптимизируют одну и ту же (не ограниченную в знаке) переменную v, которая является ценой игры. Причиной этого является то, что задача игрока В является двойственной к задаче игрока А (вам предлагается доказать это утверждение в упр. 3.5,с(6), используя определение двойственности). Это означает, что оптимальное решение одной из задач автоматически определяет оптимальное решение другой.
Пример 3.6-4
Решим следующую матричную игру методами линейного программирования.
| B1 | B2 | B3 | Минимумы строк | |
| A1 | 3 | –1 | –3 | –3 |
| A2 | –2 | 4 | –1 | –2 |
| A3 | –5 | –6 | 2 | –6 |
| Максимумы столбцов | 3 | 4 | 2 |
Значение цены игры v находится между –2 и 2.
Задача линейного программирования для игрока А
Максимизировать z = v
при ограничениях

Оптимальным решением, полученным с помощью программы TORA, является
x1 = 0.3945, х2 = 0.3119, х3 = 0.2936 и v = – 0.9083.
Соответствующими двойственными переменными являются y1 = –0.3211, у2 = –0.0826, у3 = –0.5963. Причина того, что переменные у1, у2, у3 не являются положительными, как это должно быть, заключается в том, что задача линейного программирования для игрока А является задачей максимизации с ограничениями вида "≥". При этих условиях, как известно, соответствующе двойственные переменные должны быть отрицательными. Чтобы убедиться в том, что причина именно в этом, преобразуем все ограничения вид "≥" в задаче линейного программирования для игрока А в ограничения вида "≤" путем умножения каждого неравенства на –1. Соответствующие двойственные переменные будут неотрицательными, как и требуется (см. упр. 3.6,с(1)). Действительно, построение двойственной задачи непосредственно из задачи линейного программирования для игрока А показывает (см. упр. 3.6,с(6)), что в двойственной задаче, являющейся соответствующей задачей линейного программирования для игрока В, Должны быть уj ≤ 0, но в то же время требуется выполнение условия –y1 – у2 – ... – уn = 1, что равносильно требованиям уj ≥ 0 и y1 + у2 + ... + уn = 1. К счастью, проблем, связанных со знаками, можно избежать преобразуя ограничения–неравенства вида "≥" в задаче линейного программирования для игрока А в ограничения–неравенства вида "≤".
Задача линейного программирования для игрока В
Минимизировать z = v
при ограничениях
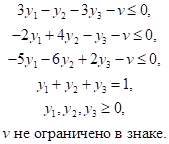
Оптимальным решением, полученным с помощью программы TORA, является
у1 = 0.3211, у2 = 0.0826, уз = 0.5963 и v = –0.9083. Соответствующими двойственными переменными являются х1 = –0.3945, х2 = –0.3119, х3 = –0.2936. Двойственные переменные отрицательны, ибо, подобно разобранной выше задаче для игрока А, в этом случае задача минимизации линейного программирования имеет ограничения–неравенства вида "≤". Приведение ограничений к виду "≥" исправит ситуацию со знаками.
Упражнений 3.6,с
1. Покажите в задаче из примера 3.6-4, что если ограничения–неравенства задачи линейного программирования для игрока А приведены к виду "≤", то аналогичные ограничения задачи для игрока В преобразуются в вид "≥" и двойственные переменные, полученные из одной или другой задачи, будут неотрицательными.
2. На загородном пикнике две команды, по два человека в каждой, играют в прятки. Есть четыре места, где можно спрятаться (А, Б, В и Г), и два члена прячущейся команды могут спрятаться каждый отдельно в любых двух из четырех мест. Затем другая команда имеет возможность проверить любые два места. Команда, которая ищет, получает премию, если будут обнаружены оба участника прячущейся команды, если же не обнаружен ни один участник, то она выплачивает премию. Иначе игра заканчивается вничью.
a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой.
b) Определите оптимальные стратегии и цену игры.
c) Имеет ли задача альтернативные решения?
d) Является ли эта игра справедливой, т.е. имеет ли она цену, равную нулю?
3. Университетские команды UA и DU определяют свои стратегии игры в национальном чемпионате по баскетболу для колледжей. Оценивая возможности своих "запасных скамеек", каждый тренер разработал по четыре варианта замены игроков на протяжении игры. Способность каждой команды выполнять двух-, трех–очковые и штрафные броски является основным фактором, определяющим результат игры. Приведенная ниже таблица содержит очки чистого выигрыша команды UA на протяжении одного владения мячом в зависимости от стратегий, планируемых каждой командой.
| DU1 | DU2 | DU3 | DU4 | |
| UA1 | 3 | –2 | 1 | 2 |
| UA2 | 2 | 3 | –3 | 0 |
| UA3 | –1 | 2 | –2 | 2 |
| UA4 | –1 | –2 | 4 | 1 |
a) Решите игру методами линейного программирования и определите выигрышные стратегии.
b) Исходя из имеющейся информации, какая из двух команд может выиграть чемпионат?
c) Пусть за всю игру имеется 60 возможностей владения мячом (30 владений для каждой команды). Предскажите ожидаемое количество очков, с которым будет выиграна игра чемпионата.
4. Армия полковника Блотто сражается с вражеской армией за контроль над двумя стратегически важными позициями. Полковник имеет в своем распоряжении два полка, а его противник — три. Каждый из противников может посыпать на любую позицию только целое число полков или совсем не посылать. Позиция будет захвачена армией, которая атакует большим количеством полков. Иначе результат сражения является ничейным
a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой и решите игр; методами линейного программирования.
b) Какая армия выиграет сражение?
5. В игре двух лиц, именуемой двухпальцевой игрой Морра, каждый игрок показывает один или два пальца и одновременно отгадывает число пальцев, которые покажет его противник. Игрок, который угадал, выигрывает сумму, равную суммарному числу показанных противниками пальцев. Иначе игра заканчивается вничью. Сформулируйте задачу в виде игры двух лиц с нулевой суммой и решите игру методами линейного программирования.
6. Покажите, что задача, двойственная к задаче линейного программирования для игрока А, является задачей линейного программирования для игрока В и что еле дующие два утверждения не противоречат друг другу.
a) Задача линейного программирования для игрока А записана в форме, приведенной в разделе 3.6.2.
b) Задача линейного программирования для игрока А записана в форме, упомянутой в п. а), в которой все ограничения вида "≥" приведены к виду "≤".
3.7. Заключение
В этой главе рассмотрены критерии выбора оптимальных решений как в ситуациях точными (детерминированными), так и неполными (вероятностными или неопределенными) данными. Дальнейшие приложения критериев выбора оптимальных решений в ситуациях с неполными данными будут рассмотрены в последующих главах. В частности, критерий ожидаемой величины используется в главах, посвященных управлению запасам) теории массового обслуживания, имитационному моделированию и марковским процесса принятия решений. Это вовсе не значит, что другие критерии неприменимы. Критерий ожидаемой величины используется скорее традиционно в силу своей простоты.
Литература
Chen S. and Hwang C. Fuzzy Multiple Decision Making, Springer – Verlag, Berlin, 1992.
Dantzing G. B. Linear Programming and Extension, Princeton University Press, Princeton, N. J., 1963.
Meyerson R. Game Theory: Analysis of Conflict, Harvard University Press, Cambridge, Mass., 1991.
Saaty T. L. Fundamentals of Decision Making, RWS Publications, Pittsburg, 1994.
Комплексные задачи
1. Руководитель цеха рассматривает три возможных решения относительно существующего фрезерного станка.
a) Модифицировать имеющийся станок, установив на нем автоматическую подачу (АП).
b) Купить новый станок с программным управлением (ПУ).
c) Заменить станок обрабатывающим центром (ОЦ).
Три альтернативы оцениваются на основе двух критериев: денежный и функциональный. Следующая таблица содержит необходимые данные.
| Критерий | Единицы | АП | ПУ | ОЦ |
| Денежный | ||||
| Начальная стоимость ($) | 12 000 | 25 000 | 120 000 | |
| Стоимость обслуживания ($) | 2 000 | 4 000 | 15 000 | |
| Стоимость обучения персонала ($) | 3 000 | 8 000 | 20 000 | |
| Функциональный | ||||
| Производительность | Изделий/день | 8 | 14 | 40 |
| Время наладки | Минут | 30 | 20 | 3 |
| Металлические отходы | Фунты/день | 440 | 165 | 44 |
Руководитель считает, что денежный критерий в полтора раза важнее функционального. Кроме того, производительность в два раза важнее времени наладки и в три раза важнее, чем количество получаемых металлических отходов. Показатель, связанный с временем наладки, считается в четыре раза важнее показателя, связанного с количеством металлических отходов. Что же касается денежного критерия, то руководитель считает, что стоимость обслуживания и стоимость обучения персонала одинаково важны, а начальная стоимость в два раза важнее каждого из этих двух показателей.
Проанализируйте описанную ситуацию и дайте соответствующие рекомендации.
2. Компания использует каталог товаров для продажи, включающий более 200 000 наименований, хранящихся на многих региональных складах. В прошлом компания считала важным иметь точный перечень запасов на каждом складе. Как следствие этого, каждый год проводился переучет — интенсивная и неприятная работа, которая неохотно выполнялась всеми складами. Компания для проверки качества складских операций в регионе сопровождала каждый переучет ревизией, которая охватывала около 100 наименований на каждом складе. Результаты проверки обнаружили, что в среднем лишь 64% наименований на каждом складе соответствовали действительной инвентарной описи, что является неприемлемым. Дабы исправить ситуацию, компания распорядилась чаще проводить переучет дорогих и быстро реализуемых товаров. Системному аналитику была поставлена задача разработать процедуры для реализации этих планов. Вместо того чтобы напрямую заняться выполнением задания компании, системный аналитик решил установить причину возникшей проблемы. Он перешел в своем исследовании от формулировки "Как мы можем увеличить частоту переучетов?" к "Как можно повысить точность переучетов?". Изучение проблемы под таким углом зрения свелось к следующему анализу. Предполагая, что доля точно сосчитанных наименований на складе равна р, аналитик затем предположил, что есть основания считать, что имеется 95%-ная вероятность того, что если изделие было правильно учтено в первый раз, то будет правильно переучтено и при последующем переучете. Для части 1 – р товаров, которая не была точно учтена в первом раунде проверки, доля правильного учета во втором раунде равна 80%. Используя эту информацию, аналитик с помощью дерева решений построил график безубыточности, который сравнил точность учета в первом и втором раундах проверки. Конечный результат сводился к тому, что склады, на которых уровень точности выше порога безубыточности, не требовали переучета. Удивительным результатом предложенного решения было рьяное усилие со стороны каждого склада сделать правильный учет за первый раз, что привело к повышению точности учета на всех складах.
Как аналитик убедил руководство в жизнеспособности предложенного порога безубыточности для повторного переучета?
3. В аэрофлоте рабочие часы устанавливаются в соответствии с договорами, заключенными с профсоюзными организациями. В частности, максимальная продолжительность работы может быть ограничена 16 часами для полетов на Боинге-74719 (В-747) и 14 часами — на Боинге-707 (В-707). Если эти пределы превышаются в силу неожиданных задержек, экипаж должен быть заменен новым. Аэрофлот содержит резервные экипажи для таких случаев. Средняя годовая стоимость содержания член» резервного экипажа оценивается в 30 000 долларов. Задержка полета на одну ночь, обусловленная отсутствием резервного экипажа, может стоить 50 000 долларов. Член экипажа находится по вызову непрерывно 12 часов в сутки 4 дня в неделю и может находиться по вызову три оставшихся дня недели. Самолет В-747 может обслуживаться двумя экипажами для самолета В-707.
Следующая таблица содержит вероятности вызова резервных экипажей, вычисленные на основании трехлетнего опыта.
| Категория рейса | Рейс (время вылета) | Вероятность вызова | |
| В – 747 | В – 707 | ||
| 1 | 14.0 | 0.014 | 0.072 |
| 2 | 13.0 | 0.000 | 0.019 |
| 3 | 12.5 | 0.000 | 0.006 |
| 4 | 12.0 | 0.016 | 0.006 |
| 5 | 11.5 | 0.003 | 0.003 |
| 6 | 11.0 | 0.002 | 0.003 |
Приведённые данные свидетельствуют, например, что для 14-часового рейса вероятность вызова равна 0.014 для В-747 и 0.072— для В-707.
Типичная пиковая часть расписания дня имеет следующий вид.
| Время дня | Самолет | Категория рейса |
| 8:00 | 707 | 3 |
| 9:00 | 707 | 6 |
| 707 | 2 | |
| 10:00 | 707 | 3 |
| 11:00 | 707 | 2 |
| 707 | 4 | |
| 15:00 | 747 | 6 |
| 16:00 | 747 | Рекомендуем посмотреть лекцию "Борьба с немцами и шведами". 4 |
| 19:00 | 747 | 1 |
Существующая политика относительно резервных экипажей состоит в использовании двух экипажей (по семь членов каждый) от 5:00 до 11:00, четырех — от 11:00 до 17:00 и двух — от 17:00 до 23:00.
Оцените эффективность Существующей политики относительно резервных экипажей. В частности, является ли число резервных экипажей очень большим, очень малым или таким, как необходимо?





















