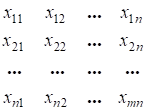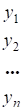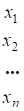Линейные экономические модели
Лекция 9. Линейные экономические модели
Модель Леонтьева многоотраслевой экономики
Эффективное ведение народного хозяйства предполагает наличие баланса между отдельными отраслями.
Предположим, что вся производящая сфера народного хозяйства разбита на некоторое число n отраслей, каждая из которых производит свой однородный продукт, причем разные отрасли производят разные продукты. Разумеется, такое представление об отрасли является в значительной мере абстракцией, так как в реальной экономике отрасль определяется не только названием выпускаемого продукта, но и ведомственной принадлежностью своих предприятий (например, данному министерству, тресту и т.п.). Однако представление об отрасли в указанном выше смысле (как «чистой» отрасли) все же полезно, так как оно позволяет провести анализ сложившейся технологической структуры народного хозяйства, изучить функционирование народного хозяйства «в первом приближении».
Итак, предполагаем, что имеется n различных отраслей O1,…,On, каждая из которых производит свой продукт. В дальнейшем отрасль Оi , будем называть «i-я отрасль». В процессе производства своего продукта каждая отрасль нуждается в продукции других отраслей (производственное потребление). Будем вести речь о некотором определенном промежутки времени [Т0, T1], (обычно таким промежутком служит плановый год) и введем следующие обозначения:
хi – общий объем продукции отрасли i за данный промежуток времени – так называемый валовой выпуск отрасли i.
xij – объем продукции отрасли i, расходуемый отраслью j в процессе производства;
уi – объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере – объем конечного потребления. Этот объем составляет обычно более 75% всей производственной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.
Рекомендуемые материалы
Указанные величины можно свести в таблицу.
Таблица 9
Показатели работы отраслей
| Производственное потребление | Конечное потребление | Валовой выпуск |
|
|
|
|
Балансовый характер этой таблицы выражается в том, что при любом i= l, ..., n должно выполняться соотношение
xi = xi1 + xi2 +...+ xin + yi, (14)
означающее, что валовой выпуск xi расходуется на производственное потребление, равное xi1 + xi2 +...+ xin, и непроизводственное потребление, равное уi. Будем называть (14) соотношениями баланса.
Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки, киловатт-часы и т.п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевой балансы. Для определенности в дальнейшем будем иметь в виду (если не оговорено противное) стоимостной баланс.
В. Леонтьев, рассматривая развитие американской экономики в предвоенный период, обратил внимание на важное обстоятельство. А именно, величины  остаются постоянными в течение ряда лет. Это обуславливается примерным постоянством используемой технологии.
остаются постоянными в течение ряда лет. Это обуславливается примерным постоянством используемой технологии.
В соответствии со сказанным сделаем такое допущение: для выпуска любого объема хj продукции отрасли j необходимо затратить продукцию отрасли i в качестве aijxj , где аij – постоянный коэффициент. Проще говоря, материальные издержки пропорциональны объему производимой продукции. Это допущение постулирует, как говорят, линейность существующей технологии. Принцип линейности распространяется и на другие виды издержек. Например, на оплату труда, а также на нормативную прибыль. Итак, согласно гипотезе линейности имеем
xij = aij xj(i, j =1, ..., n). (15)
Коэффициенты аij называют коэффициентами прямых затрат (коэффициент материалоемкости).
В предположении линейности соотношения (14) принимают вид:
x1 = a11x1 + a12x2 + … +a1n xn + y1
x2 = a21x1 + a22x2 + … +a2n xn + y2
…………………………………..
xn = an1x1 + an2x2 + … +ann xn + yn,
или, в матричной записи,
 , (16)
, (16)
где
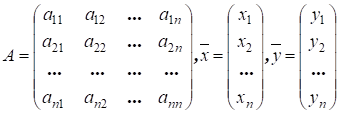
Вектор  называется вектором валового выпуска, вектор
называется вектором валового выпуска, вектор  – вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (16) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов
– вектором конечного потребления, а матрица А – матрицей прямых затрат. Соотношение (16) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов  и
и  это соотношение называют также моделью Леонтьева.
это соотношение называют также моделью Леонтьева.
Уравнения межотраслевого баланса можно использовать для целей планирования. В этом случае задача ставится так: для предстоящего планового периода [T0,T1] задается вектор  конечного потребления. Требуется определить вектор
конечного потребления. Требуется определить вектор  валового выпуска. Проще говоря, нужно решить задачу: сколько следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В этом случае необходимо решить систему линейных уравнений (16) с неизвестным вектором
валового выпуска. Проще говоря, нужно решить задачу: сколько следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В этом случае необходимо решить систему линейных уравнений (16) с неизвестным вектором  при заданных матрице А и вектору
при заданных матрице А и вектору  . При этом нужно иметь в виду следующие особенности системы (16):
. При этом нужно иметь в виду следующие особенности системы (16):
1. Все компоненты матрицы А и вектора  неотрицательны (это вытекает из экономического смысла А и
неотрицательны (это вытекает из экономического смысла А и  ). Для краткости будем говорить о неотрицательности самой матрицы А и вектора
). Для краткости будем говорить о неотрицательности самой матрицы А и вектора  и записывать это так:
и записывать это так:  .
.
2. Все компоненты вектора  также должны быть неотрицательными:
также должны быть неотрицательными:  .
.
Замечание. Обратим внимание на смысл коэффициентов аij прямых затрат в случае стоимостного (а не натурального) баланса. В этом случае из (16) видно, что aij совпадает со значением хij при xj = 1 (1 руб.).
Таким образом, аij есть стоимость продукции отрасли i, вложенной в 1 руб. продукции отрасли j. Отсюда, между прочим, видно, что стоимостной подход по сравнению с натуральным обладает более широкими возможностями, при таком подходе уже необязательно рассматривать «чистые», т. е. однопродуктовые, отрасли. Ведь и в случае многопродуктовых отраслей тоже можно говорить о стоимостном вкладе одной отрасли в выпуск 1 руб. продукции другой отрасли; скажем, о вкладе промышленной сферы в выпуск 1 руб. сельскохозяйственной продукции или о вкладе промышленной группы А (производство предметов потребления). Вместе с тем надо понимать, что планирование исключительно в стоимостных величинах может легко привести к дисбалансу потоков материально-технического снабжения.
Пример 31. Таблица 10 содержит данные баланса трех отраслей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить, соответственно, до 60, 70и 30 условных денежных единиц.
Таблица 10
Показатели работы 3 отраслей
| № п/п | Отрасль | Потребление | Конечный продукт | Валовый выпуск | ||
| 1 | 2 | 3 | ||||
| 1 2 3 | Добыча и переработка углеводородов Энергетика Машиностроение | 5 10 20 | 35 10 10 | 20 20 10 | 40 60 10 | 100 100 50 |
Решение. Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат. Согласно формуле (9.1), имеем:
 ,
,  ,
,  .
.
Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь
 . (9.2)
. (9.2)
Требуется найти новый вектор валового выпуска  , удовлетворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты
, удовлетворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты  неизвестного вектора
неизвестного вектора  находятся из системы уравнений, которая в матричной форме имеет следующий вид:
находятся из системы уравнений, которая в матричной форме имеет следующий вид:
 , или
, или  . (9.3)
. (9.3)
Матрица этой системы
 .
.
Решение системы линейных уравнений (9.3) при заданном векторе правой части (9.12) (например, методом Гаусса) дает новый вектор  как решение уравнений межотраслевого баланса:
как решение уравнений межотраслевого баланса:
 .
.
Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 52,2 %, уровень энергетики – на 35,8 % и выпуск машиностроения – на 85 % – по сравнению с исходными величинами, указанными в табл. 9.2.
Продуктивные модели Леонтьева
Определение. Матрица А ³ 0 называется продуктивной, если для любого вектора  ³ 0 существует решение
³ 0 существует решение  ³ 0 уравнения (9.1)
³ 0 уравнения (9.1)
 (13)
(13)
В этом случае модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.
Итак, модель Леонтьева продуктивна, если любой вектор  ³ 0 конечного потребления можно получить при валовом выпуске
³ 0 конечного потребления можно получить при валовом выпуске  ³ 0.
³ 0.
Нижеследующая теорема 1 показывает, что нет необходимости требовать существования решения  ³ 0 уравнения (9.1) для любого вектора
³ 0 уравнения (9.1) для любого вектора  ³ 0. Достаточно, чтобы такое решение существовало хотя бы для одного вектора
³ 0. Достаточно, чтобы такое решение существовало хотя бы для одного вектора  ³ 0.
³ 0.
Условимся в дальнейшем писать  ³ 0 и называть вектор
³ 0 и называть вектор  положительным, если все компоненты этого вектора строго положительны.
положительным, если все компоненты этого вектора строго положительны.
Теорема 9.1 (первый критерий продуктивности.) Если А ³ 0 и для некоторого положительного вектора  * уравнение (7.3) имеет решение
* уравнение (7.3) имеет решение  * ³ 0, то матрица А продуктивна.
* ³ 0, то матрица А продуктивна.
Заметим, что на самом деле  > 0, что следует из
> 0, что следует из  * = А
* = А * +
* +  * и А ³ 0,
* и А ³ 0,  *³ 0,
*³ 0,  * ³ 0.
* ³ 0.
Уравнение Леонтьева (9.1) можно записать следующим образом:
(Е - А)  =
=  , (9.4)
, (9.4)
где Е - единичная матрица.
Возникает, естественно, вопрос об обращении матрицы Е - А.
Понятно, что если обратная матрица (Е - А)-1 существует, то из (9.4) вытекает
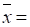 (Е - А)-1
(Е - А)-1 (9.5)
(9.5)
Следующая теорема дает более эффективное условие продуктивности, чем теорема 9.1
Теорема 9.2 (второй критерий продуктивности). Матрица А ³ 0 продуктивна тогда и только тогда, когда матрица (Е – А)-1 существует и неотрицательна.
Доказательство. Если (Е – А)-1 существует и ³ 0, то из формулы (9.5) следует продуктивность матрицы А.
Обратно, пусть матрица А продуктивна, Рассмотрим следующие системы уравнений:
(Е – А) 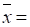
 , (Е – А)
, (Е – А)  ,..., (Е – А)
,..., (Е – А)  , где е1, е2,…, еn – столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т.е. существуют такие векторы (столбцы)
, где е1, е2,…, еn – столбцы единичной матрицы. Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение, т.е. существуют такие векторы (столбцы)  ³ 0,
³ 0,  ³ 0,...,
³ 0,...,  ³ 0, что
³ 0, что
(Е – А)  =
=  , (Е – А)
, (Е – А) =
=  ,..., (Е – А)
,..., (Е – А)  =
=  . (9.6)
. (9.6)
Обозначим через С матрицу, составленную из столбцов с1,с2,...,сп. Тогда вместо п равенств (9.6) можно написать одно: (Е – А)С = Е.
Следовательно, матрица (Е – А) имеет обратную С, причем С ³ 0. Теорема доказана.
Пример 32. Исследуем на продуктивность матрицу
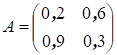
В данном случае
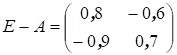
Необходимые вычисления предоставим читателю провести самостоятельно. Получаем матрицу (Е – А)-1, которая существует и равна
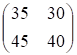
Мы видим, что эта матрица неотрицательна. Следовательно, А продуктивна.
Теорема 3. (третий критерий продуктивности). Матрица А ³ 0 продуктивна тогда и только тогда, когда сходиться бесконечный ряд.
Е + А + А2 + ... (9.7)
Полученный нами критерий продуктивности матрицы А (сходимость ряда (9.7)) в ряде случаев может быть использован для проверки матрицы А на продуктивность. Покажем, например, что если сумма элементов любого столбца неотрицательной матрицы А меньше 1*, то А продуктивна. Действительно, пусть q - наибольшая из указанных сумм, q <1. Ясно, что тогда все элементы матрицы А не превосходят q. Из правила перемножения матриц легко вывести, что любой элемент матрицы А2 не превосходит q2:
(A2)ij = ai1ajl + ai2aj2 +...+ ainanj £ q (ai1 +...+ anj) < q2 <1.
Точно так же получим, что элементы матрицы А3 не превосходит q3 и т.д. Отсюда следует сходимость ряда (9.7), а значит, и продуктивность матрицы А.
Например для матрицы
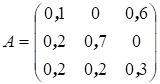
сумма элементов каждого столбца меньше единицы. Следовательно, А продуктивна.
Аналогично доказывается, что если в неотрицательной матрице А сумма элементов любой строки меньше 1, то матрица А продуктивна. Впрочем, то же самое можно вывести и из следующего предложения: если продуктивна матрица А, то продуктивна и матрица Ат ,что следует из теоремы 2.
Пусть А  0 – продуктивная матрица. Запасом продуктивности матрицы А назовем такое число
0 – продуктивная матрица. Запасом продуктивности матрицы А назовем такое число  , что все матрицы
, что все матрицы  , где 1<
, где 1< <1 +
<1 +  , продуктивны, а матрица (1+
, продуктивны, а матрица (1+ )А – не продуктивна.
)А – не продуктивна.
Пример 33. Выяснить, какой запас продуктивности имеет матрица А из примера 30.
Решение. Будем руководствоваться критерием продуктивности из теоремы 2 (существование неотрицательной матрицы (Е – А)-1). В данном случае
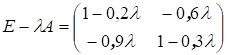
Определитель этой матрицы
 .
.
Обратной матрицей будет
 .
.
Для продуктивности  нужно, чтобы все элементы обратной матрицы были неотрицательны, т.е.
нужно, чтобы все элементы обратной матрицы были неотрицательны, т.е.  ,
,  ,
,  . Имеем
. Имеем  при
при  ,
,  . Отсюда матрица
. Отсюда матрица  продуктивной при
продуктивной при  , т.е.
, т.е.  . Запас продуктивности матрицы А равен 0,015.
. Запас продуктивности матрицы А равен 0,015.
Задания для самостоятельной работы
Задача 1. Отрасль состоит из четырех предприятий: вектор выпуска продукции и матрица коэффициентов прямых затрат имеют вид
 ,
,  .
.
Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.
Задача 2. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в табл. 9.3.
Таблица 9.3
Данные по выпуску продукции
| Вид сырья | Расход сырья по видам продукции, вес. ед./изд. | Запас сырья, вес. ед. | ||
| 1 | 2 | 3 | ||
| 1 2 3 | 5 10 9 | 12 6 11 | 7 8 4 | 2350 2060 2270 |
Найти объем выпуска продукции каждого вида при заданных запасах сырья.
Задача 3. В условиях примера 2 из 2.3.3 определить прирост объемов валовых выпусков по каждой отрасли (в процентах), если конечное потребление увеличить по отраслям, соответственно, на 30, 10 и 50 %. Решить задачу методом обратной матрицы и методом Гаусса.
Задача 4. Исследовать на продуктивность матрицу
 .
.
Найти запас продуктивности.
Лекция 10. Линейные экономические модели:
модель равновесных цен, модель международной торговли
Модель равновесных цен
Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева – так называемую модель равновесных цен. Пусть, как и прежде, А - матрица прямых затрат,  (xl, x2,...,xn) – вектор валового выпуска. Обозначим через
(xl, x2,...,xn) – вектор валового выпуска. Обозначим через  (р1, р2, …рn – вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда, например, первая отрасль получит доход, равный p1, х1.
(р1, р2, …рn – вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда, например, первая отрасль получит доход, равный p1, х1.
Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли в объеме a11, второй отрасли в объеме а21, n-й отрасли в объеме an1 т. д. На покупку этой продукции ею будет затрачена сумма, равная a11 p1 + a21 p2 +...+ anl pn. Следовательно, для выпуска продукции в объеме х1 первой отрасли необходимо потратить на закупку продукции других отраслей сумму равную x1(a11p1 + a21p2 +...+ an1pn). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим V1 (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Таким образом, имеет место следующее равенство:
x1 p1 = x1 (a11 p1 +a21 p2 +… +an1 pn) + V1.
Разделив это равенство на х1 получаем
p1 = (a11 p1 +a21 p2 +… +an1 pn) + v1,
где v1  – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
– норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
Подобным же образом получаем для остальных отраслей
p2 = a12 p1 + a22 p2 + … + an2 pn +v2
……………………………………
pn = a1n p1 + a2n p2 +…+ ann pn +v2
Найденные равенства могут быть записаны в матричной форме следующим образом:
 , (9.8)
, (9.8)
где  - вектор норм добавленной стоимости.
- вектор норм добавленной стоимости.
Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева с той лишь разницей, что  заменен на
заменен на ,
, – на
– на , А – на Ат.
, А – на Ат.
Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей. Она также позволяет прогнозировать изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Пример 34. Рассмотрим экономическую систему, состоящую из трех отраслей. Назовем их условно: топливно-энергетическая отрасль, промышленность и сельское хозяйство. Пусть
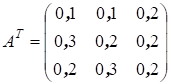
- транспонированная матрица прямых затрат,  = (4;10;4)
= (4;10;4)
- вектор норм добавленной стоимости.
Определим равновесные цены. Для этого, как и в модели Леонтьева, воспользуемся формулой (9.8):
 ,
,
где СТ = (Е - АТ)-1 транспонированная матрица полных затрат.
После необходимых вычислений имеем
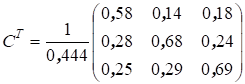
Отсюда получаем, что  .
.
Допустим теперь, что в топливно-энергетической отрасли произойдет увеличение нормы добавленной стоимости на 1,11. Определим равновесные цены в этом случае. Принимая во внимание, что  (5,11;10;4), находим, что
(5,11;10;4), находим, что
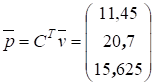
Таким образом, продукция первой отрасли подорожала на 14,5 %, второй - на 3,5% третьей отрасли - на 4,17%. Нетрудно также, зная объемы выпуска, подсчитать вызванную этим повышением инфляцию.
Модель международной торговли.
Собственные векторы и собственные значения матриц
Модель международной торговли (кратко: модель обмена) служит для ответа на следующий вопрос: какими должны быть соотношения между государственными бюджетами стран, торгующих между собой, чтобы торговля была взаимовыгодной, т.е. не было значительного дефицита торгового баланса для каждой из стран- участниц.
Проблема достаточно важна, так как дефицит в торговле между странами порождает такие явления, как лицензии, квоты, таможенные пошлины и даже торговые войны.
Для простоты изложения рассмотрим три страны-участницы торговли с государственными бюджетами Х1, Х2, Х3, которые условно назовем США, Германия, и Кувейт. Будем считать, что весь госбюджет каждой страны тратится на закупки товаров либо внутри страны, либо на импорт из других стран. Пусть, скажем, США тратят половину своего бюджета на закупку товаров внутри страны,  бюджета – на товары из Германии, оставшуюся
бюджета – на товары из Германии, оставшуюся  бюджета – на товары из Кувейта. Кувейт, в свою очередь, тратит
бюджета – на товары из Кувейта. Кувейт, в свою очередь, тратит  бюджета на закупки в Германии и ничего не закупает внутри страны.
бюджета на закупки в Германии и ничего не закупает внутри страны.
Введем структурную матрицу торговли:
США Германия Кувейт
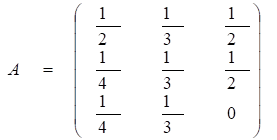
Вообще, пусть аij – часть госбюджета, которую j-я стана тратит на закупки товаров i-й страны. Заметим, что сумма элементов матрицы А в каждом столбце равна единице.
После подведения итогов торговля за год страна под номером i получит выручку pi = ai1X1 + ai2X2 + ai3X3. Например, США будут иметь выручку
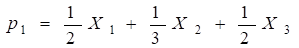
доля США доля Германии доля Кувейта
Для того чтобы торговля была сбалансированной, необходимо потребовать бездефицитность торговли для каждой страны:
 для всех i
для всех i
Предложение 1. Условием бездефицитной торговли являются равенства p = Xi, i = 1,2,3.
В матричной форме утверждение, содержащееся в предложении 1, выглядит следующим образом:
АХ = Х, (9.9)
где
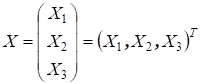
Обобщая равенства (9.9) рассмотрим следующее.
Определение 10.1. Ненулевой вектор  называется собственным вектором квадратной матрицы А порядка n, если
называется собственным вектором квадратной матрицы А порядка n, если
 (9.10)
(9.10)
где  – некоторое число.
– некоторое число.
При этом число  называется собственным значением матрицы А. Говорят так:
называется собственным значением матрицы А. Говорят так:  есть собственный вектор матрицы А, принадлежащий ее собственному значению
есть собственный вектор матрицы А, принадлежащий ее собственному значению  .
.
Пример 35. Найдем собственные векторы и собственные значения следующей матрицы порядка 2:
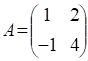
Положим  – вектор - столбец. Тогда из соотношения (9.10) следует, что
– вектор - столбец. Тогда из соотношения (9.10) следует, что
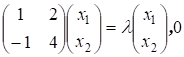
т.е.
 ,
,
или
 , (9.11)
, (9.11)
Если вектор  – собственный, то это означает, что однородная система уравнений (9.11) имеет ненулевое решение. Согласно последней теореме это условие эквивалентно тому, что определитель системы (9.11) равен нулю.
– собственный, то это означает, что однородная система уравнений (9.11) имеет ненулевое решение. Согласно последней теореме это условие эквивалентно тому, что определитель системы (9.11) равен нулю.
 ,
,
или  . Таким образом, собственными значениями матрицы А будут числа 2 и 3.
. Таким образом, собственными значениями матрицы А будут числа 2 и 3.
Найдем соответствующие собственные векторы. Подставим  =2 и
=2 и  =3 в систему (9.11)
=3 в систему (9.11)
 =2
=2  =3
=3

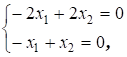

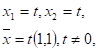
Однородная система уравнений  тогда и только тогда имеет ненулевое решение, когда ее определитель равен нулю:
тогда и только тогда имеет ненулевое решение, когда ее определитель равен нулю:
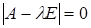
Если раскрыть данный определитель, как в рассмотренном примере (9.11), то получится многочлен степени п относительно  , называемый характеристическим многочленом матрицы А.
, называемый характеристическим многочленом матрицы А.
Определение 10.2. Уравнение
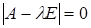
называется характеристическим уравнением матрицы А.
Таким образом, собственные значения матрицы А являются корнями ее характеристического уравнения.
Пример 36. Найти собственные значения собственные векторы матрицы.
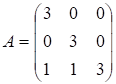
Запишем характеристическое уравнение:
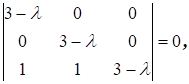
или  . Следовательно,
. Следовательно,  – единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводиться к единственному уравнению:
– единственное собственное значение матрицы А. Система уравнений для отыскания собственных векторов сводиться к единственному уравнению:
х1 + х2=0,
т.е. собственный вектор х = (–а, а, b) представляется в виде линейной комбинации
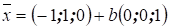
двух линейно независимых векторов  и
и  .
.
Вернемся к отысканию собственного вектора X в модели международной торговли. Система уравнений для нахождения X имеет вид (9.9) т.е.

 = 0.
= 0.
Нетрудно найти общее решение этой системы:
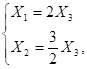
поэтому в качестве собственного вектора можно взять вектор
 (4; 3; 2)
(4; 3; 2)
В частности, это означает, что сбалансированность торговли этих трех стран может быть достигнута только в том случае, когда госбюджеты находятся в отношении
X1: X2: X3 = 4: 3: 2
Определение. Максимальное по модулю собственное значение неотрицательной матрицы А называется числом Фробениуса матрицы А, а соответствующий ему неотрицательный собственный вектор - вектором Фробениуса для А.
Понятие собственного значения, а также понятие вектора Фробениуса неотрицательной матрицы А позволяют по- новому подойти к вопросу о продуктивности модели Леонтьева.
Теорема. Неотрицательная квадратная матрица А продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.
Люди также интересуются этой лекцией: 8 Приложения.
Задания для самостоятельной работы
Экономическая система состоит из 3 отраслей: топливно-энергетическая, промышленность, сельское хозяйство. Пусть
 –
–
– транспонированная матрица прямых затрат,  – вектор норм добавленной стоимости.
– вектор норм добавленной стоимости.
1. Определить равновесные цены.
2. Определить равновесные цены, если произойдет увеличение нормы добавленной стоимости на 1,1 в топливно-энергетической отрасли.