Нелинейная регрессия
§ 9. Нелинейная регрессия . Метод линеаризации .
В параграфе 4 мы уже познакомились с некоторыми вариантами нелинейных регрессий. Сейчас немного подробнее об этом.
Нелинейные регрессии подразделяют на два больших класса:
1. Квазилинейные регрессии (нелинейные по факторам, но линейные по коэффициентам.
2. Собственно нелинейные регрессии (нелинейные и по факторам, и по коэффициентам)
Примеры:
Квазилинейные регрессии:
y = a lnx + b
y = a 
+ b
Рекомендуемые материалы
y = 
+ b
y = a x2 + b x + c
Во всех этих соотношениях коэффициенты стоят в первой степени, т.е. формулы линейны по коэффициентам.
Собственно нелинейные регрессии:
y = a е b x
y = a xb
(нелинейные по факторам, но линейные по Для линейной регрессии была получена простая нормальная система для коэффициентов
y = ax + b a ( x2 ) + b ( x ) = xy (22)
a ( x ) + b ( 1 ) = y
Пусть корреляционное поле показывает , что зависимость должна быть нелинейной . Нужно попытаться сделать такую замену переменных , чтобы в новых переменных зависимость стала линейной .И тогда коэффициенты корреляционной зависимости будут определяться из системы уравнений (22) .
 |
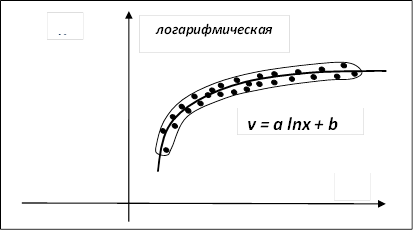Примеры :
1)
Сделаем замену : 
После этого уравнение регрессии становится линейным: 
и можно пользоваться всеми соотношениями, полученными для линейной регрессии. Нужно только с самого начала пересчитать исходные данные для фактора Х.
X X1 (=lnx)
| x1 |
| (x1)1 |
| x2 |
| (x1)2 |
| x3 |
| (x1)3 |
| . . . . |
| . . . . . |
| xn |
| (x1)n |
2)
Чтобы уравнение стало линейным, нужно убрать из показателя степени коэффициент b. Единственный способ это сделать – логарифмировать обе части равенства:
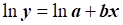
Сделаем замены : 
; 
; 
.
После этого уравнение регрессии становится линейным: 
.
Нужно пересчитать исходные данные для фактора Y, и потом, когда коэффициенты регрессии 
будут найдены, вернуться назад к коэффициентам 
.
3)
 |
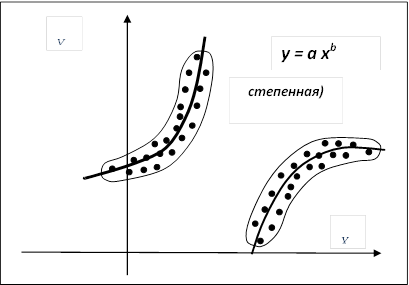Линеаризация проводится логарифмированием.
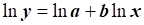
Сделаем замены : ; ;
; .
После этого уравнение регрессии становится линейным: 
.
4) Гиперболическая зависимость : 
Сделаем замену : 
и получим линейное уравнение 
.
5) Логистическая зависимость (с явлением перегиба с насыщением) : 
.
Сначала перейдем к обратным величинам
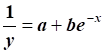
Затем делаем замены:
Основные принципы разработки инвестиционной стратегии в условиях кризиса - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
; 
;
; .
и получаем линейное уравнение .
Общее замечание:
Для квазилинейных регрессий замену и линеаризацию можно сделать всегда.
Для собственно нелинейных регрессий это совсем не обязательно.
