Статистический анализ
Власов М. П.
конспект лекций по дисциплине
Компьютерные методы статистического анализа и прогнозирование
ТЕМА 3 Статистический анализ
Содержание
стр.
1. Ковариационный анализ …………………………………………….. 2
2. Дисперсия и дисперсионный анализ ……………………..…………. 5
Рекомендуемые материалы
3. Многомерный статистический анализ …………………………….. 11
4.Факторный анализ …………………………………………………… 21
Санкт-Петербург 2008
1. Ковариационный анализ
Ковариационная матрица образуется из попарных ковариаций нескольких случайных величин. Для  -мерного случайного вектора
-мерного случайного вектора  ковариационная матрица является квадратной матрицей
ковариационная матрица является квадратной матрицей  ,
,  с компонентами
с компонентами
 .
.
На главной диагонали ковариационной матрицы находятся дисперсии величин  , т.е.
, т.е.  . Все ковариационные матрицы являются симметричными (т.е.
. Все ковариационные матрицы являются симметричными (т.е.  ) и неотрицательно определёнными. Если ковариационная матрица положительно определена, то распределение
) и неотрицательно определёнными. Если ковариационная матрица положительно определена, то распределение  называют невырожденным. Для оценки
называют невырожденным. Для оценки  по выборке
по выборке  (где
(где  ), используют выборочную ковариационную матрицу
), используют выборочную ковариационную матрицу 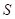
 ,
,
где  — вектор-столбец арифметических средних
— вектор-столбец арифметических средних  . Если случайные векторы
. Если случайные векторы  имеют нормальное распределение с ковариационной матрицей
имеют нормальное распределение с ковариационной матрицей  , то
, то 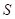 является оценкой максимального правдоподобия для
является оценкой максимального правдоподобия для  .
.
Ковариационный анализ представлен совокупностью методов и результатов, относящихся к математико-статистическому анализу моделей. Эти модели предназначены для исследования зависимости среднего значения некоторого количественного результирующего показателя  от набора неколичественных факторов
от набора неколичественных факторов  и одновременно от набора количественных (регрессионных или сопутствующих) переменных
и одновременно от набора количественных (регрессионных или сопутствующих) переменных  . Результирующий признак
. Результирующий признак  может быть векторным (тогда говорят о многомерном ковариационном анализе).
может быть векторным (тогда говорят о многомерном ковариационном анализе).
Неколичественные факторы  задают сочетания условий (качественной природы), в которых производилась фиксация каждого из наблюдений (экспериментальных значений)
задают сочетания условий (качественной природы), в которых производилась фиксация каждого из наблюдений (экспериментальных значений)  и
и  , и описываются обычно с помощью т. н. индикаторных переменных. Среди индикаторных и сопутствующих переменных могут быть, как случайные, так и не случайные (контролируемые в эксперименте).
, и описываются обычно с помощью т. н. индикаторных переменных. Среди индикаторных и сопутствующих переменных могут быть, как случайные, так и не случайные (контролируемые в эксперименте).
Основные теоретические и прикладные разработки по ковариационному анализу относятся к линейным моделям. В частности, если анализируется схема из  наблюдений со скалярным результирующим признаком
наблюдений со скалярным результирующим признаком  , с
, с  возможными типами условий эксперимента и с
возможными типами условий эксперимента и с  сопутствующими переменными
сопутствующими переменными  , то линейная модель соответствующего ковариационного анализа задаётся уравнениями:
, то линейная модель соответствующего ковариационного анализа задаётся уравнениями:
 ,
,  , (1.1)
, (1.1)
где индикаторные переменные  , если условие
, если условие  эксперимента имело место при наблюдении
эксперимента имело место при наблюдении  , и равны нулю — в противном случае; коэффициенты
, и равны нулю — в противном случае; коэффициенты  - определяют эффект влияния условия
- определяют эффект влияния условия  ;
;  — значение сопутствующей переменной
— значение сопутствующей переменной  , при котором наблюдался результирующий признак
, при котором наблюдался результирующий признак  (
( ;
;  );
);  — значения соответствующих коэффициентов регрессии
— значения соответствующих коэффициентов регрессии  по
по  вообще говоря, зависящие от конкретного сочетания условий эксперимента, т. е. от вектора
вообще говоря, зависящие от конкретного сочетания условий эксперимента, т. е. от вектора  , а
, а  - величина остаточных случайных компонент («ошибок измерения»), имеющих нулевые средние значения. Основное содержание ковариационного анализа — в построении статистических оценок для неизвестных параметров
- величина остаточных случайных компонент («ошибок измерения»), имеющих нулевые средние значения. Основное содержание ковариационного анализа — в построении статистических оценок для неизвестных параметров  ;
;  и статистических критериев, предназначенных для проверки различных гипотез относительно значений этих параметров.
и статистических критериев, предназначенных для проверки различных гипотез относительно значений этих параметров.
Если в (1.1) постулировать априори  , то получится модель дисперсионного анализа; если же из (3.1) исключить влияние неколичественных факторов (т. е. положить
, то получится модель дисперсионного анализа; если же из (3.1) исключить влияние неколичественных факторов (т. е. положить  ), то получится линейная модель регрессионного анализа. Своим названием ковариационный анализ обязан тому обстоятельству, что в его вычислениях используются разбиения ковариаций переменных
), то получится линейная модель регрессионного анализа. Своим названием ковариационный анализ обязан тому обстоятельству, что в его вычислениях используются разбиения ковариаций переменных  и
и  точно так же, как в дисперсионном анализе используются разбиения остаточной суммы квадратов.
точно так же, как в дисперсионном анализе используются разбиения остаточной суммы квадратов.
Считается, что термин «ковариационный анализ» введён английским статистиком Р. А. Фишером в связи с рассмотрением одной частной схемы этой модели в § 49 144-го издания книги •«Статистические методы для исследователей» (пер. с англ., М., 1958).
Для оценивания неизвестных значений параметров и проверки гипотез в линейной модели ковариационного анализа (1.1), запишем её в матричном виде:
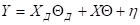
или
 (1.1”.)
(1.1”.)
где  — вектор-столбец наблюдений результирующего показателя;
— вектор-столбец наблюдений результирующего показателя;  — матрица плана эксперимента по неколичественным факторам
— матрица плана эксперимента по неколичественным факторам  ;
;
 — вектор-столбец неизвестных параметров, соответствующих неколичественным факторам (общее среднее, главные эффекты, взаимодействия и т. п.);
— вектор-столбец неизвестных параметров, соответствующих неколичественным факторам (общее среднее, главные эффекты, взаимодействия и т. п.);
 —- матрица плана регрессионных (количественных) объясняющих переменных;
—- матрица плана регрессионных (количественных) объясняющих переменных;
 — вектор-столбец параметров (неизвестных коэффициентов регрессии);
— вектор-столбец параметров (неизвестных коэффициентов регрессии);
 — вектор-столбец случайных остатков модели, подчиняющийся нормальному распределению
— вектор-столбец случайных остатков модели, подчиняющийся нормальному распределению  , где остаточная дисперсия
, где остаточная дисперсия  неизвестна (подлежит оцениванию). Предполагается, что тип условий эксперимента
неизвестна (подлежит оцениванию). Предполагается, что тип условий эксперимента  («способ обработки» — в исходной терминологии дисперсионного анализа) не влияет на матрицу плана регрессионных экспериментов
(«способ обработки» — в исходной терминологии дисперсионного анализа) не влияет на матрицу плана регрессионных экспериментов  , т. е. столбцы матрицы X линейно не зависят от столбцов матрицы
, т. е. столбцы матрицы X линейно не зависят от столбцов матрицы  (существенное предположение). К несущественным предположениям относятся допущения о том, что матрицы
(существенное предположение). К несущественным предположениям относятся допущения о том, что матрицы  и
и  имеют полный ранг (соответственно
имеют полный ранг (соответственно  и
и  ) и что не имеется ограничении на параметры
) и что не имеется ограничении на параметры  . Запись (
. Запись ( ), где
), где  и
и  - матрицы с одинаковым количеством строк, означает матрицу, полученную присоединением столбцов матрицы
- матрицы с одинаковым количеством строк, означает матрицу, полученную присоединением столбцов матрицы  к столбцам матрицы
к столбцам матрицы  . Аналогично
. Аналогично  — это матрица, полученная присоединением к строкам матрицы
— это матрица, полученная присоединением к строкам матрицы  строк матрицы
строк матрицы  (где
(где  и
и  — матрицы с одинаковым количеством столбцов). Существенное отличие моделей (1.1)-(1.1”) от внешне похожих на них моделей регрессионного и классического ковариационного анализа — в зависимости коэффициентов
— матрицы с одинаковым количеством столбцов). Существенное отличие моделей (1.1)-(1.1”) от внешне похожих на них моделей регрессионного и классического ковариационного анализа — в зависимости коэффициентов  от неколичественных переменных
от неколичественных переменных  . В этом случае анализ моделей осуществляется с помощью специальных методов расщепления смесей.
. В этом случае анализ моделей осуществляется с помощью специальных методов расщепления смесей.
Для нахождения оценок  и
и  неизвестных параметров
неизвестных параметров  и
и  можно было бы формально рассмотреть (1.1') как одну большую модель регрессии и применить к ней обычный метод наименьших квадратов. Однако можно добиться существенного упрощения анализа за счёт использования специального строения матрицы (
можно было бы формально рассмотреть (1.1') как одну большую модель регрессии и применить к ней обычный метод наименьших квадратов. Однако можно добиться существенного упрощения анализа за счёт использования специального строения матрицы ( ) и знаний специфики модели дисперсионного анализа.
) и знаний специфики модели дисперсионного анализа.
2. Дисперсия и дисперсионный анализ
Дисперсия это мера  случайного рассеивания значений случайно величины
случайного рассеивания значений случайно величины  от её математического ожидания
от её математического ожидания  , определяемая равенством
, определяемая равенством
 .
.
Когда говорят о дисперсии случайной величины  , всегда предполагают, что существует математическое ожидание
, всегда предполагают, что существует математическое ожидание  , при этом дисперсия
, при этом дисперсия  может существовать (т. е. быть конечной) или не существовать (т. е. быть бесконечной). Для дискретной случайной величины
может существовать (т. е. быть конечной) или не существовать (т. е. быть бесконечной). Для дискретной случайной величины  , принимающей не более чем счётное число различных значений
, принимающей не более чем счётное число различных значений  с вероятностями
с вероятностями
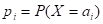
 ,
,
если  имеет плотность распределения
имеет плотность распределения  , то
, то
 ,
,
в общем случае
 ,
,
где  — функция распределения случайной величины
— функция распределения случайной величины  и интеграл понимается в смысле Лебега —Стильтьеса или Римана — Стильтьеса.
и интеграл понимается в смысле Лебега —Стильтьеса или Римана — Стильтьеса.
Помимо дисперсии можно рассматривать и другие меры отклонения случайной величины от её математического ожидания, например  ,
,  и т.д., а также меры, основанные на квантилях. Важность дисперсии объясняется той ролью, которую играет это понятие для предельных теорем теории вероятностей и в математической статистике при обработке наблюдений. В качестве оценки
и т.д., а также меры, основанные на квантилях. Важность дисперсии объясняется той ролью, которую играет это понятие для предельных теорем теории вероятностей и в математической статистике при обработке наблюдений. В качестве оценки  дисперсии
дисперсии  по выборке
по выборке  независимых наблюдений, распределение которых совпадает с распределением
независимых наблюдений, распределение которых совпадает с распределением  , рассматривают
, рассматривают
 ,
,  .
.
Из определения дисперсии (и из свойств математического ожидания) можно вывести следующие её свойства:
а)  (
( — некоторая неслучайная величина);
— некоторая неслучайная величина);
б)  ;
;
в)  (
( и
и  — некоторые неслучайные величины);
— некоторые неслучайные величины);
г)  .
.
Часто для обозначения дисперсии используют греческую букву «сигма» (в квадрате), т.е. записывают  .
.
Дисперсионный анализ это статистический метод, предназначенный для выявления влияния нескольких одновременно действующих факторов на исследуемый показатель (наблюдаемую величину). Термин «Дисперсионный анализ» был введён в статистическую практику английским статистиком Р. Фишером (1925) и изначально этот анализ широко использовался при проведении сельскохозяйственных экспериментов. Современные приложения дисперсионного анализа охватывают широкий круг задач экономики, социологии, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях.
Дисперсионный анализ обычно подразумевает, что эксперимент организован в соответствии с планом, позволяющим при сравнительно малом числе измерений независимо оценить влияние каждого из факторов на измеряемый количественный показатель. Сами факторы могут быть и качественными и количественными. Применение дисперсионного анализа при пассивных наблюдениях, например, в экономике, подразумевает надлежащий отбор групп данных из более богатой совокупности данных.
В основе дисперсионного анализа лежит следующая вероятностная модель:
 ,
,  (2.1)
(2.1)
где  — неизвестные параметры, отражающие влияние переменной
— неизвестные параметры, отражающие влияние переменной  на измеряемую величину
на измеряемую величину  , индекс
, индекс  помечает номер измерения. Ошибки
помечает номер измерения. Ошибки  предполагаются случайными величинами с нулевыми средними, постоянной дисперсией
предполагаются случайными величинами с нулевыми средними, постоянной дисперсией  и независимыми в совокупности. Большинство теоретических результатов в дисперсионном анализе развиты для ошибок, распределённых по нормальному закону.
и независимыми в совокупности. Большинство теоретических результатов в дисперсионном анализе развиты для ошибок, распределённых по нормальному закону.
В дисперсионном анализе переменные  принимают целочисленные значения, обычно это 0 и 1. При непрерывном изменении этих факторов (2.1) относится к регрессионному анализу. Если в (2.1) входят факторы обоих видов, то говорят о ковариационном анализе. Очевидно, что все три случая поглощаются регрессионным анализом. Однако, учёт структуры переменных позволяет развить методы статистически более прозрачные и вычислительно более удобные.
принимают целочисленные значения, обычно это 0 и 1. При непрерывном изменении этих факторов (2.1) относится к регрессионному анализу. Если в (2.1) входят факторы обоих видов, то говорят о ковариационном анализе. Очевидно, что все три случая поглощаются регрессионным анализом. Однако, учёт структуры переменных позволяет развить методы статистически более прозрачные и вычислительно более удобные.
Иногда в (2.1) предполагается, что параметры  — случайные величины. Тогда говорят о модели со случайными факторами. Термин «смешанная модель» применяют, когда в (2.1) входят случайные и постоянные параметры
— случайные величины. Тогда говорят о модели со случайными факторами. Термин «смешанная модель» применяют, когда в (2.1) входят случайные и постоянные параметры  .
.
Однофакторный анализ, несмотря на свою простоту, иллюстрирует основные идеи дисперсионный анализа. Модель (2.1) можно записать в следующем виде:
 ,
, ,
,  , (2.2)
, (2.2)
где вместо одного индекса  введено два
введено два  (поэтому
(поэтому  помечено одним индексом),
помечено одним индексом),  удовлетворяет тем же требованиям, что
удовлетворяет тем же требованиям, что  . Одной из наиболее популярных «нулевых» гипотез
. Одной из наиболее популярных «нулевых» гипотез  , проверяемых в рамках дисперсионного анализа, является гипотеза о равенстве всех
, проверяемых в рамках дисперсионного анализа, является гипотеза о равенстве всех  . Параметр
. Параметр  может быть, например, истолкован как производительность предприятия
может быть, например, истолкован как производительность предприятия  , урожайность сорта
, урожайность сорта  какой-либо сельскохозяйственной культуры и т. д.
какой-либо сельскохозяйственной культуры и т. д.
Очевидно, что (2.2) может быть проанализировано в рамках регрессионного анализа через оценивание параметров  . Подобный подход приводит хотя и к простым, но довольно громоздким вычислениям и требует обращения к понятию функции, допускающей оценку. Этот факт, по-видимому, и способствовал развитию дисперсионного анализа (расцвет дисперсионного анализа относится к докомпьютерной эре). Основная идея проверки гипотезы
. Подобный подход приводит хотя и к простым, но довольно громоздким вычислениям и требует обращения к понятию функции, допускающей оценку. Этот факт, по-видимому, и способствовал развитию дисперсионного анализа (расцвет дисперсионного анализа относится к докомпьютерной эре). Основная идея проверки гипотезы  заключается в следующем:
заключается в следующем:
строятся две независимые оценки дисперсии случайной величины  одна из которых предполагает выполнение гипотезы
одна из которых предполагает выполнение гипотезы  , а другая — нет. Затем составляется их отношение, которое должно иметь центральное
, а другая — нет. Затем составляется их отношение, которое должно иметь центральное  -распределение при выполнении
-распределение при выполнении  и нецентральное
и нецентральное  -распределение с параметром нецентральности, определяемым разбросом (дисперсией) параметров
-распределение с параметром нецентральности, определяемым разбросом (дисперсией) параметров  .
.
Можно показать, что такими двумя оценками являются:
 ,
,
 ,
,
где  ,
,  ,
,  , т. е. отношение
, т. е. отношение
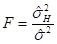
имеет  -распределение с
-распределение с  и
и  степенями свободы. Параметр нецентральности равен:
степенями свободы. Параметр нецентральности равен:
 ,
,
 .
.
По  -критерию гипотеза
-критерию гипотеза  отвергается с уровнем значимости
отвергается с уровнем значимости  , если
, если  . Параметр
. Параметр  определяет мощность
определяет мощность  -критерия, однако он полезен скорее для более глубокого понимания задачи проверки гипотезы, нежели для практических выводов, т. к.
-критерия, однако он полезен скорее для более глубокого понимания задачи проверки гипотезы, нежели для практических выводов, т. к.  неизвестны.
неизвестны.
Во многих исследованиях по дисперсионному анализу вместо записи (3.2) предполагают использовать представление:
 ,
,  . (2.3.)
. (2.3.)
Гипотеза  предполагает теперь, что все
предполагает теперь, что все  равны. Данное представление более удобно при рассмотрении задач многофакторного дисперсионного анализа.
равны. Данное представление более удобно при рассмотрении задач многофакторного дисперсионного анализа.
Многофакторный анализ. Предположим, что анализируя производительность предприятия  нужно оценить эффект использования технологии
нужно оценить эффект использования технологии  . Тогда по аналогии с (3.3) целесообразно рассмотреть следующую модель:
. Тогда по аналогии с (3.3) целесообразно рассмотреть следующую модель:
 ,
,
 ,
,  ,
,  . (2.4.)
. (2.4.)
Отсюда можно выписать аналоги (2.1) и (2.2). Константа ( называется парным взаимодействием факторов
называется парным взаимодействием факторов  и
и  .
.
Очевидно, что в рамках (2.4) естественным образом можно сформулировать довольно много гипотез, достойных экспериментальной проверки. Наиболее популярны следующие:
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ,
,  .
.
Например, гипотеза  может трактоваться как гипотеза о несущественности того, на каком предприятии какая технология используется для производства.
может трактоваться как гипотеза о несущественности того, на каком предприятии какая технология используется для производства.
Идея проверки гипотез так же, как и в однофакторном анализе, состоит в построении независимых оценок для дисперсии случайной величины  причём оценки конструируются в предположении справедливости или гипотезы
причём оценки конструируются в предположении справедливости или гипотезы  , или
, или  , или
, или  , или
, или  и
и  вместе и т. д.
вместе и т. д.
Сравнивая (2.3) и (2.4), можно построить модели и для большего числа факторов. Следует лишь иметь в виду, что при нескольких факторах можно (но необязательно) ввести тройные, четверные и т. д. взаимодействия. Обычно независимо от количества анализируемых факторов ограничиваются лишь парными взаимодействиями.
В отличие от однофакторного случая при многофакторном дисперсионном анализа не любое распределение наблюдений  по ячейкам (i,j...) позволяет конструировать независимые оценки для
по ячейкам (i,j...) позволяет конструировать независимые оценки для  при различных гипотезах. Задача разумного выбора
при различных гипотезах. Задача разумного выбора  составляет один из важнейших (и старейших) разделов математической теории планирования эксперимента. Особый практический интерес эта задача представляет при значительном количестве факторов. Предположив, что в каждой из ячеек
составляет один из важнейших (и старейших) разделов математической теории планирования эксперимента. Особый практический интерес эта задача представляет при значительном количестве факторов. Предположив, что в каждой из ячеек  ... проводятся
... проводятся  наблюдений, легко убедиться в необходимости
наблюдений, легко убедиться в необходимости  ... наблюдений для реализации всего эксперимента. Использование специальных планов позволяет резко сократить количество необходимых наблюдений.
... наблюдений для реализации всего эксперимента. Использование специальных планов позволяет резко сократить количество необходимых наблюдений.
3. Многомерный статистический анализ
Многомерный статистический анализ это раздел математической статистики, посвященный математическим методам построения оптимальных планов сбора, систематизации, обработки и интерпретации многомерных статистических данных, нацеленным, в первую очередь, на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практических выводов. Под многомерным признаком понимается  -мерный вектор
-мерный вектор  показателей (признаков, переменных)
показателей (признаков, переменных)  , среди которых могут быть: количественные, т. е. скалярно измеряющие в определённой шкале степень проявления изучаемого свойства объекта; порядковые (или ординальные), т.е. позволяющие упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства; классификационные (или номинальные), т. е. позволяющие разбивать исследуемую совокупность объектов на не поддающиеся упорядочиванию однородные (по анализируемому свойству) классы. Результаты измерения этих показателей
, среди которых могут быть: количественные, т. е. скалярно измеряющие в определённой шкале степень проявления изучаемого свойства объекта; порядковые (или ординальные), т.е. позволяющие упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства; классификационные (или номинальные), т. е. позволяющие разбивать исследуемую совокупность объектов на не поддающиеся упорядочиванию однородные (по анализируемому свойству) классы. Результаты измерения этих показателей
 (3.1.)
(3.1.)
на каждом из  объектов исследуемой совокупности образуют последовательность многомерных наблюдений, или исходный массив многомерных данных для проведения многомерного статистического анализа. Значительная часть многомерного статистического анализа обслуживает ситуации, в которых исследуемый многомерный признак интерпретируется как многомерная случайная величина и, соответственно, последовательность многомерных наблюдений (3.1) — как выборка из генеральной совокупности. В этом случае выбор методов обработки исходных статистических данных и анализ их свойств производится на основе тех или иных допущений относительно природы многомерного (совместного) закона распределения вероятностей
объектов исследуемой совокупности образуют последовательность многомерных наблюдений, или исходный массив многомерных данных для проведения многомерного статистического анализа. Значительная часть многомерного статистического анализа обслуживает ситуации, в которых исследуемый многомерный признак интерпретируется как многомерная случайная величина и, соответственно, последовательность многомерных наблюдений (3.1) — как выборка из генеральной совокупности. В этом случае выбор методов обработки исходных статистических данных и анализ их свойств производится на основе тех или иных допущений относительно природы многомерного (совместного) закона распределения вероятностей  .
.
По содержанию многомерный статистический анализ может быть условно разбит на три основных подраздела:
· многомерный статистический анализ многомерных распределений и их основных характеристик;
· многомерный статистический анализ характера и структуры взаимосвязей между компонентами исследуемого многомерного признака;
· многомерный статистический анализ геометрической структуры исследуемой совокупности многомерных наблюдений.
Многомерный статистический анализ многомерных распределений и их основных характеристик охватывает лишь ситуации, в которых обрабатываемые наблюдения (3.1.) имеют вероятностную природу, т.е. интерпретируются как выборка из соответствующей генеральной совокупности. К основным задачам этого подраздела относятся:
· статистическое оценивание исследуемых многомерных распределений, их главных числовых характеристик и параметров;
· исследование свойств используемых статистических оценок;
· исследование распределений вероятностей для ряда статистик, с помощью которых строятся статистические критерии проверки различных гипотез о вероятностной природе анализируемых многомерных данных.
Основные результаты относятся к частному случаю, когда исследуемый признак  подчинён многомерному нормальному закону распределения
подчинён многомерному нормальному закону распределения  , функция плотности которого
, функция плотности которого  задаётся соотношением
задаётся соотношением
 (3.2.)
(3.2.)
где  — вектор математических ожиданий компонент случайной величины
— вектор математических ожиданий компонент случайной величины  , т.е.
, т.е.  ,
,  , a
, a  — ковариационная матрица случайного вектора
— ковариационная матрица случайного вектора  , т.е.
, т.е.  — ковариации компонент вектора
— ковариации компонент вектора  (рассматривается невырожденный случай, когда ранг
(рассматривается невырожденный случай, когда ранг  ; в противном случае, т. е. при ранге
; в противном случае, т. е. при ранге  , вce результаты остаются справедливыми, но применительно к подпространству меньшей размерности
, вce результаты остаются справедливыми, но применительно к подпространству меньшей размерности  , в которой оказывается сосредоточенным распределение вероятностей исследуемого случайного вектора
, в которой оказывается сосредоточенным распределение вероятностей исследуемого случайного вектора  ).
).
Так, если (3.1.) — последовательность независимых наблюдений, образующих случайную выборку из  , то оценками максимального правдоподобия для параметров
, то оценками максимального правдоподобия для параметров  и
и  , участвующих в (3.2.), являются соответственно статистики
, участвующих в (3.2.), являются соответственно статистики
 (3.3.)
(3.3.)
и
 , (3.4.)
, (3.4.)
причём случайный вектор  подчиняется
подчиняется  -мерному нормальному закону
-мерному нормальному закону  и не зависит от
и не зависит от  , а совместное распределение элементов матрицы
, а совместное распределение элементов матрицы  описывается т. н. распределением Уишарта, плотность которого
описывается т. н. распределением Уишарта, плотность которого
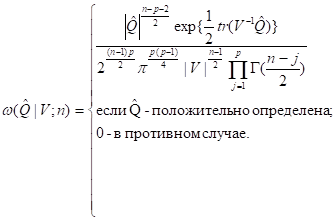
В рамках этой же схемы исследованы распределения и моменты таких выборочных характеристик многомерной случайной величины, как коэффициенты парной, частной и множественной корреляции, обобщённая дисперсия (т. е. статистика  ), обобщённая
), обобщённая  — статистика Хотеллинга. В частности, если определить в качестве выборочной ковариационной матрицы
— статистика Хотеллинга. В частности, если определить в качестве выборочной ковариационной матрицы  подправленную «на несмещённость» оценку
подправленную «на несмещённость» оценку  , а именно
, а именно
 ,
,
то распределение случайной величины  стремится к
стремится к  при
при  , а случайные величины
, а случайные величины
 (3.6.)
(3.6.)
и
 (3.7.)
(3.7.)
подчиняются  -распределениям с числами степеней свободы соответственно
-распределениям с числами степеней свободы соответственно  и
и  . В соотношении (3.7.)
. В соотношении (3.7.)  и
и  — объёмы двух независимых выборок вида (3.1.), извлечённых из одной и той же генеральной совокупности
— объёмы двух независимых выборок вида (3.1.), извлечённых из одной и той же генеральной совокупности  — оценки вида (3.3.) и (3.4.) —(3.5.), построенные по выборке
— оценки вида (3.3.) и (3.4.) —(3.5.), построенные по выборке  , а
, а
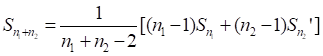
— общая выборочная ковариационная матрица, построенная по оценкам  и
и  .
.
Многомерный статистический анализ характера и структуры взаимосвязей компонент исследуемого многомерного признака объединяет в себе понятия и результаты, обслуживающие такие методы и модели многомерного статистического анализа, как множественная регрессия, многомерный дисперсионный анализ и ковариационный анализ, факторный анализ и метод главных компонент, анализ канонических корреляций. Результаты, составляющие содержание этого подраздела, могут быть условно разделены на два основных типа.
1) Построение наилучших (в определённом смысле) статистических оценок для параметров упомянутых моделей и анализ их свойств (точности, а в вероятностной постановке — законов их распределения, доверительных областей и т. д.). Так, пусть исследуемый многомерный признак  интерпретируется как векторная случайная величина, подчинённая
интерпретируется как векторная случайная величина, подчинённая  -мерному нормальному распределению
-мерному нормальному распределению  , и расчленён на два подвектора-столбца
, и расчленён на два подвектора-столбца  и
и  размерности
размерности  и
и  соответственно. Это определяет и соответствующее расчленение вектора математических ожиданий
соответственно. Это определяет и соответствующее расчленение вектора математических ожиданий  , теоретической и выборочной ковариационных матриц
, теоретической и выборочной ковариационных матриц  и
и  , а именно:
, а именно:
 ,
,  и
и  .
.
Тогда условное распределение подвектора  (при условии, что второй подвектор принял фиксированное значение
(при условии, что второй подвектор принял фиксированное значение  будет также нормальным
будет также нормальным  . При этом оценками максимального правдоподобия
. При этом оценками максимального правдоподобия  и
и  для матриц регрессионных коэффициентов
для матриц регрессионных коэффициентов  и ковариаций
и ковариаций  этой классической многомерной модели множественной регрессии
этой классической многомерной модели множественной регрессии
 (3.8.)
(3.8.)
будут взаимно независимые статистики соответственно
 и
и  ;
;
здесь распределение оценки  подчинено нормальному закону
подчинено нормальному закону  , а оценки
, а оценки  — закону Уишарта с параметрами
— закону Уишарта с параметрами  и
и  (элементы ковариационной матрицы
(элементы ковариационной матрицы  выражаются в терминах элементов матрицы
выражаются в терминах элементов матрицы  ).
).
Основные результаты по построению оценок параметров и исследованию их свойств в моделях факторного анализа, главных компонент и канонических корреляций относятся к анализу вероятностно-статистических свойств собственных (характеристических) значений и векторов различных выборочных ковариационных матриц.
В схемах, не укладывающихся в рамки классической нормальной модели, и тем более в рамки какой-либо вероятностной модели, основные результаты относятся к построению алгоритмов (и исследованию их свойств) вычисления оценок параметров, наилучших с точки зрения некоторого экзогенно заданного функционала качества (или адекватности) модели.
2) Построение статистических критериев для проверки различных гипотез о структуре исследуемых взаимосвязей. В рамках многомерной нормальной модели (последовательности наблюдений вида (3.1.) интерпретируются как случайные выборки из соответствующих многомерных нормальных генеральных совокупностей) построены, например, статистические критерии для проверки следующих гипотез.
I. Гипотезы  о равенстве вектора математических ожиданий исследуемых показателей заданному конкретному вектору
о равенстве вектора математических ожиданий исследуемых показателей заданному конкретному вектору  ; проверяются с помощью
; проверяются с помощью  -статистики Хотеллинга с подстановкой в формулу (3.6.)
-статистики Хотеллинга с подстановкой в формулу (3.6.)  .
.
II. Гипотезы  о равенстве векторов математических ожиданий в двух генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных двумя выборками; проверяются с помощью статистики
о равенстве векторов математических ожиданий в двух генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных двумя выборками; проверяются с помощью статистики  .
.
III. Гипотезы  о равенстве векторов математических ожиданий в нескольких генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных своими выборками; проверяются с помощью статистики
о равенстве векторов математических ожиданий в нескольких генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных своими выборками; проверяются с помощью статистики
 ,
,
в которой  есть
есть  -мерное наблюдение
-мерное наблюдение  в выборке объёма
в выборке объёма  , представляющей генеральную совокупность
, представляющей генеральную совокупность  , а
, а  и
и  — оценки вида (3.3.), построенные соответственно отдельно по каждой из выборок и по объединённой выборке объёма
— оценки вида (3.3.), построенные соответственно отдельно по каждой из выборок и по объединённой выборке объёма  .
.
IV. Гипотезы  и
и  об эквивалентности нескольких нормальных генеральных совокупностей, представленных своими выборками
об эквивалентности нескольких нормальных генеральных совокупностей, представленных своими выборками  ,
,  , проверяются с помощью статистики
, проверяются с помощью статистики
 ,
,
в которой  — оценка вида (4.4), построенная отдельно по наблюдениям выборки
— оценка вида (4.4), построенная отдельно по наблюдениям выборки  ,
,  .
.
V. Гипотезы о взаимной независимости подвекторов - столбцов  размерностей соответственно
размерностей соответственно  , на которые расчленён исходный
, на которые расчленён исходный  -мерный вектор исследуемых показателей
-мерный вектор исследуемых показателей  ,
,  ; проверяются с помощью статистики
; проверяются с помощью статистики
 ,
,
в которой  и
и  — выборочные ковариационные матрицы вида (3.4.) для всего вектора
— выборочные ковариационные матрицы вида (3.4.) для всего вектора  и для его подвектора
и для его подвектора  соответственно.
соответственно.
Многомерный статистический анализ геометрической структуры исследуемой совокупности многомерных наблюдений объединяет в себе понятия и результаты таких моделей и схем, как дискриминантный анализ, смеси вероятностных распределений, кластер-анализ и таксономия, многомерное шкалирование. Узловым во всех этих схемах является понятие расстояния (меры близости, меры сходства) между анализируемыми элементами. При этом анализируемыми могут быть как реальные объекты, на каждом из которых фиксируются значения показателей  , — тогда геометрическим образом обследованного объекта
, — тогда геометрическим образом обследованного объекта  будет точка
будет точка  в соответствующем
в соответствующем  -мерном пространстве, так и сами показатели
-мерном пространстве, так и сами показатели  ,
,  — тогда геометрическим образом показателя
— тогда геометрическим образом показателя  будет точка
будет точка  в соответствующем
в соответствующем  -мерном пространстве.
-мерном пространстве.
Методы и результаты дискриминантного анализа направлены на решение следующей задачи. Известно о существовании определённого числа  генеральных совокупностей и имеется по одной выборке из каждой совокупности («обучающие выборки»). Требуется построить основанное на имеющихся обучающих выборках наилучшее в определённом смысле классифицирующее правило, позволяющее приписать некоторый новый элемент (наблюдение
генеральных совокупностей и имеется по одной выборке из каждой совокупности («обучающие выборки»). Требуется построить основанное на имеющихся обучающих выборках наилучшее в определённом смысле классифицирующее правило, позволяющее приписать некоторый новый элемент (наблюдение  ) к своей генеральной совокупности в ситуации, когда заранее неизвестно, к какой из совокупностей этот элемент принадлежит. Обычно под классифицирующим правилом понимается последовательность действий: по вычислению скалярной функции от исследуемых показателей, по значениям которой принимается решение об отнесении элемента к одному из классов (построение дискриминантной функции); по упорядочению самих показателей по степени их информативности с точки зрения правильного отнесения элементов к классам; по вычислению соответствующих вероятностей ошибочной классификации.
) к своей генеральной совокупности в ситуации, когда заранее неизвестно, к какой из совокупностей этот элемент принадлежит. Обычно под классифицирующим правилом понимается последовательность действий: по вычислению скалярной функции от исследуемых показателей, по значениям которой принимается решение об отнесении элемента к одному из классов (построение дискриминантной функции); по упорядочению самих показателей по степени их информативности с точки зрения правильного отнесения элементов к классам; по вычислению соответствующих вероятностей ошибочной классификации.
Задача анализа смесей распределений вероятностей чаще всего (но не всегда) возникает также в связи с исследованием «геометрической структуры» рассматриваемой совокупности. При этом понятие однородного класса  формализуется с помощью генеральной совокупности, описываемой некоторым (как правило, унимодальным) законом распределения
формализуется с помощью генеральной совокупности, описываемой некоторым (как правило, унимодальным) законом распределения  , так что распределение общей генеральной совокупности, из которой извлечена выборка (4.1.), описывается смесью распределений вида
, так что распределение общей генеральной совокупности, из которой извлечена выборка (4.1.), описывается смесью распределений вида
 ,
,
где  — априорная вероятность (удельный вес элементов) класса
— априорная вероятность (удельный вес элементов) класса  в общей генеральной совокупности. Задача состоит в «хорошем» статистическом оценивании (по выборке
в общей генеральной совокупности. Задача состоит в «хорошем» статистическом оценивании (по выборке  ) неизвестных параметров
) неизвестных параметров  0Г, а иногда и
0Г, а иногда и  . Это, в частности, позволяет свести задачу классификации элементов к схеме дискриминантного анализа, хотя в данном случае отсутствовали обучающие выборки.
. Это, в частности, позволяет свести задачу классификации элементов к схеме дискриминантного анализа, хотя в данном случае отсутствовали обучающие выборки.
Методы и результаты кластер-анализа (классификация, таксономии, распознавания образов «без учителя») направлены на решение следующей задачи. Геометрическая структура анализируемой совокупности элементов задана либо координатами соответствующих точек (т.е. матрицей  ,
,  ,
,  ), либо набором геометрических характеристик их взаимного расположения, например, матрицей попарных расстояний
), либо набором геометрических характеристик их взаимного расположения, например, матрицей попарных расстояний  . Требуется разбить исследуемую совокупность элементов на сравнительно небольшое (заранее известное или нет) число классов так, чтобы элементы одного класса находились на небольшом расстоянии друг от друга, в то время как разные классы были бы по возможности достаточно взаимоудалены один от другого и не разбивались бы на столь удалённые друг от друга части.
. Требуется разбить исследуемую совокупность элементов на сравнительно небольшое (заранее известное или нет) число классов так, чтобы элементы одного класса находились на небольшом расстоянии друг от друга, в то время как разные классы были бы по возможности достаточно взаимоудалены один от другого и не разбивались бы на столь удалённые друг от друга части.
Задача многомерного шкалирования относится к ситуации, когда исследуемая совокупность элементов задана с помощью матрицы попарных расстояний  и заключается в приписывании каждому из элементов заданного числа
и заключается в приписывании каждому из элементов заданного числа  координат таким образом, чтобы структура попарных взаимных расстояний между элементами, измеренных с помощью этих вспомогательных координат, в среднем наименее отличались бы от заданной. Следует заметить, что основные результаты и методы кластер-анализа и многомерного шкалирования развиваются обычно без каких-либо допущений о вероятностной природе исходных данных.
координат таким образом, чтобы структура попарных взаимных расстояний между элементами, измеренных с помощью этих вспомогательных координат, в среднем наименее отличались бы от заданной. Следует заметить, что основные результаты и методы кластер-анализа и многомерного шкалирования развиваются обычно без каких-либо допущений о вероятностной природе исходных данных.
Прикладное значение многомерного статистического анализа состоит в основном в обслуживании следующих трёх проблем.
Проблема статистического исследования зависимостей между анализируемыми показателями. Предполагая, что исследуемый набор статистически регистрируемых показателей  разбит, исходя из содержательного смысла этих показателей и окончательных целей исследования, на
разбит, исходя из содержательного смысла этих показателей и окончательных целей исследования, на  -мерный подвектор
-мерный подвектор  предсказываемых (зависимых) переменных и
предсказываемых (зависимых) переменных и  -мерный подвектор
-мерный подвектор  предсказывающих (независимых) переменных, можно сказать, что проблема состоит в определении на основании выборки (3.1.) такой
предсказывающих (независимых) переменных, можно сказать, что проблема состоит в определении на основании выборки (3.1.) такой  -мерной векторной функции
-мерной векторной функции  из класса допустимых решений
из класса допустимых решений  , которая давала бы наилучшую, в определённом смысле, аппроксимацию поведения подвектора показателей
, которая давала бы наилучшую, в определённом смысле, аппроксимацию поведения подвектора показателей  . В зависимости от конкретного вида функционала качества аппроксимации и природы анализируемых показателей приходят к тем или иным схемам множественной регрессии, дисперсионного, ковариационного или конфлюентного анализа.
. В зависимости от конкретного вида функционала качества аппроксимации и природы анализируемых показателей приходят к тем или иным схемам множественной регрессии, дисперсионного, ковариационного или конфлюентного анализа.
Проблема классификации элементов (объектов или показателей) в общей (нестрогой) постановке заключается в том, чтобы всю анализируемую совокупность элементов, статистически представленную в виде матрицы  ,
,  ,
,  , или матрицы
, или матрицы  ,
,  , разбить на сравнительно небольшое число однородных, в определённом смысле, групп. В зависимости от природы априорной информации и конкретного вида функционала, задающего критерий качества классификации, приходят к тем или иным схемам дискриминантного анализа, кластер-анализа (таксономии, распознавания образов «без учителя»), расщепления смесей распределений.
, разбить на сравнительно небольшое число однородных, в определённом смысле, групп. В зависимости от природы априорной информации и конкретного вида функционала, задающего критерий качества классификации, приходят к тем или иным схемам дискриминантного анализа, кластер-анализа (таксономии, распознавания образов «без учителя»), расщепления смесей распределений.
Проблема снижения размерности исследуемого факторного пространства и отбора наиболее информативных показателей заключается в определении такого набора сравнительно небольшого числа  показателей
показателей  , найденного в классе допустимых преобразований
, найденного в классе допустимых преобразований  исходных показателей
исходных показателей  , на котором достигается верхняя грань некоторой экзогенно заданной меры информативности
, на котором достигается верхняя грань некоторой экзогенно заданной меры информативности  -мерной системы признаков. Конкретизация функционала, задающего меру автоинформативности (т. е. нацеленного на максимальное сохранение информации, содержащейся в статистическом массиве (4.1.) относительно самих исходных признаков), приводит, в частности, к различным схемам факторного анализа и главных компонент, к методам экстремальной группировки признаков. Функционалы, задающие меру внешней информативности, т. е. нацеленные на извлечение из (3.1.) максимальной информации относительно некоторых других, не содержащихся непосредственно в
-мерной системы признаков. Конкретизация функционала, задающего меру автоинформативности (т. е. нацеленного на максимальное сохранение информации, содержащейся в статистическом массиве (4.1.) относительно самих исходных признаков), приводит, в частности, к различным схемам факторного анализа и главных компонент, к методам экстремальной группировки признаков. Функционалы, задающие меру внешней информативности, т. е. нацеленные на извлечение из (3.1.) максимальной информации относительно некоторых других, не содержащихся непосредственно в  показателей или явлений, приводят к различным методам отбора наиболее информативных показателей в схемах статистического исследования зависимостей и дискриминантного анализа.
показателей или явлений, приводят к различным методам отбора наиболее информативных показателей в схемах статистического исследования зависимостей и дискриминантного анализа.
Основной математический инструментарий многомерного статистического анализа составляют специальные методы теории систем линейных уравнений и теории матриц (методы решения простой и обобщённой задачи о собственных значениях и векторах; простое обращение и псевдообращение матриц; процедуры диагонализации матриц и т. д.) и некоторые оптимизационные алгоритмы (методы покоординатного спуска, сопряжённых градиентов, ветвей и границ, различные версии случайного поиска и стохастической аппроксимации и т. д.).
4. Факторный анализ
Факторный анализ представляет совокупность методов построения математических моделей, позволяющих восстановить предполагаемую структуру, лежащую в основе наблюдаемых данных, для их описания в сжатом и интерпретируемом виде. Под структурой понимается небольшое число ненаблюдаемых переменных, называемых факторами, а также их количественное преобразование в наблюдаемые переменные (показатели, признаки, индексы и т. п.). В общем случае ни число факторов, ни их количественные значения для наблюдений, ни вид их преобразований в наблюдаемые переменные не известны и должны определяться в результате факторного анализа только из наблюдаемых данных. Таким образом, факторный анализ позволяет количественно описать предполагаемый механизм порождения наблюдаемых данных. Математические модели факторного анализа, имеющие вероятностную природу, относятся к многомерному статистическому анализу и факторный анализ является его разделом. В противном случае факторный анализ — раздел. Рассмотрим следующий простой физический пример (задача о цилиндрах). Предположим, что 12 переменных - функции радиуса основания ( ) и высоты
) и высоты  ) 30 прямых круговых цилиндров. Каждой переменной соответствует формула:
) 30 прямых круговых цилиндров. Каждой переменной соответствует формула:
1. Диагональ ( )
)
 .
.
2. Площадь основания ( )
)
 .
.
3. Площадь боковой поверхности ( )
)
 .
.
4. Площадь полной поверхности ( )
)
 .
.
5. Объём ( )
)
 .
.
6. Полнота ( )
)
 .
.
7. Угол между диагональю и основанием ( )
)
 .
.
8. Угол между диагональю и боковой поверхностью ( )
)
 .
.
9. Момент инерции ( )
)
 .
.
10. Электросопротивление ( )
)
 .
.
11. Электропроводность ( )
)
 .
.
12. Деформация кручения ( )
)
 .
.
Здесь все функции нелинейные и содержат степени и тригонометрические преобразования. Сначала случайным образом зададим радиус основания  и высоту
и высоту  30 цилиндров (например, сгенерировав 60 случайных чисел). Эти 60 чисел можно представить в виде матрицы размера 30x2. Затем по формулам преобразования
30 цилиндров (например, сгенерировав 60 случайных чисел). Эти 60 чисел можно представить в виде матрицы размера 30x2. Затем по формулам преобразования  и
и  в 12 переменных
в 12 переменных  получим вторую матрицу данных 30x12. Далее на 12 переменных каждого цилиндра наложим независимые нормальные ошибки с нулевым средним и заданными дисперсиями. В результате получим третью матрицу данных 30x12. Все 12 переменных физически значимы и, в принципе, их можно измерить фактически, причём с некоторой ошибкой измерения. В этом примере истинная структура, лежащая в основе третьей матрицы данных 30x12, известна и представляет собой две основные переменные (радиус основания и высота цилиндров), их истинные значения для 30 цилиндров, а также функции преобразования радиуса и высоты в 12 переменных. Факторный анализ применяется к третьей матрице данных 30x12 для восстановления истинной структуры, порождающей эти данные. При этом предполагается, что ни число основных переменных, ни их значения для 30 наблюдений, ни вид функций преобразования не известны и требуют определения. Причём не предполагается даже, что наблюдаемые данные относятся к цилиндрам. Структура, полученная в результате факторного анализа, сравнивается с истинной. Сравнение показывает очень хорошее соответствие восстановленной и истинной структур.
получим вторую матрицу данных 30x12. Далее на 12 переменных каждого цилиндра наложим независимые нормальные ошибки с нулевым средним и заданными дисперсиями. В результате получим третью матрицу данных 30x12. Все 12 переменных физически значимы и, в принципе, их можно измерить фактически, причём с некоторой ошибкой измерения. В этом примере истинная структура, лежащая в основе третьей матрицы данных 30x12, известна и представляет собой две основные переменные (радиус основания и высота цилиндров), их истинные значения для 30 цилиндров, а также функции преобразования радиуса и высоты в 12 переменных. Факторный анализ применяется к третьей матрице данных 30x12 для восстановления истинной структуры, порождающей эти данные. При этом предполагается, что ни число основных переменных, ни их значения для 30 наблюдений, ни вид функций преобразования не известны и требуют определения. Причём не предполагается даже, что наблюдаемые данные относятся к цилиндрам. Структура, полученная в результате факторного анализа, сравнивается с истинной. Сравнение показывает очень хорошее соответствие восстановленной и истинной структур.
Предполагаемый механизм порождения наблюдаемых данных в классической линейной модели факторного анализа описывается следующим образом:
 , (4.1)
, (4.1)
где  -
-  случайный вектор наблюдаемых величин,
случайный вектор наблюдаемых величин,
 ,
,  (здесь
(здесь  - знак математического ожидания);
- знак математического ожидания);
 -
-  неизвестная матрица нагрузок общих факторов на наблюдаемые величины;
неизвестная матрица нагрузок общих факторов на наблюдаемые величины;
 —
—  (
( ) ненаблюдаемый случайный вектор общих факторов,
) ненаблюдаемый случайный вектор общих факторов,  ,
,  (иногда
(иногда  интерпретируется как вектор неизвестных взаимно ортогональных нормированных неслучайных параметров);
интерпретируется как вектор неизвестных взаимно ортогональных нормированных неслучайных параметров);
 —
—  случайный вектор ошибок или, т. н., специфических факторов,
случайный вектор ошибок или, т. н., специфических факторов,  ,
,  ,
,  , где
, где  - неизвестная диагональная ковариационная матрица. Из модели (6.1.) следует, что
- неизвестная диагональная ковариационная матрица. Из модели (6.1.) следует, что
 . (4.2.)
. (4.2.)
Параметры  и
и  , общие для всех наблюдений, называются структурными, а значения вектора
, общие для всех наблюдений, называются структурными, а значения вектора  , связанные с отдельными наблюдениями значений случайного вектора
, связанные с отдельными наблюдениями значений случайного вектора  , называются случайными параметрами. При
, называются случайными параметрами. При  на
на  необходимо наложить
необходимо наложить  независимых ограничений, иначе её элементы не определены, так как в (4.1)
независимых ограничений, иначе её элементы не определены, так как в (4.1)  можно заменить на
можно заменить на  , а
, а  на
на  , где
, где  — любая
— любая  невырожденная матрица, и соотношение (4.2.) останется справедливым. Эта неопределённость устраняется применением целого ряда критериев, которые можно рассматривать как ограничения, накладываемые на модель факторного анализа.
невырожденная матрица, и соотношение (4.2.) останется справедливым. Эта неопределённость устраняется применением целого ряда критериев, которые можно рассматривать как ограничения, накладываемые на модель факторного анализа.
Вращение факторных осей в линейной модели (4.1.) - это умножение справа  матрицы факторных нагрузок
матрицы факторных нагрузок  на невырожденную действительную матрицу
на невырожденную действительную матрицу  порядка
порядка  , соответствующее выбору новой системы координат (новых факторных осей) в пространстве общих факторов (т. е. в
, соответствующее выбору новой системы координат (новых факторных осей) в пространстве общих факторов (т. е. в  -мерном подпространстве, натянутом на столбцы матрицы
-мерном подпространстве, натянутом на столбцы матрицы  как на
как на  векторов в исходном
векторов в исходном  -мерном пространстве) с целью наилучшей содержательной интерпретации общих факторов (например, в смысле простой структуры Тэрстоуна); тогда
-мерном пространстве) с целью наилучшей содержательной интерпретации общих факторов (например, в смысле простой структуры Тэрстоуна); тогда  вектор
вектор  задаёт координаты точки на этих новых факторных осях. Вращение факторных осей называется ортогональным, если
задаёт координаты точки на этих новых факторных осях. Вращение факторных осей называется ортогональным, если  - ортогональная матрица, и косоугольным - в противном случае. Для вращения факторных осей существуют два подхода в зависимости от того, сформулировано ли оно в алгебраических или геометрических терминах. Первый подход связан с аналитическими методами, второй - с графическим изображением осей, которые проводятся через облака (скопления) точек.
- ортогональная матрица, и косоугольным - в противном случае. Для вращения факторных осей существуют два подхода в зависимости от того, сформулировано ли оно в алгебраических или геометрических терминах. Первый подход связан с аналитическими методами, второй - с графическим изображением осей, которые проводятся через облака (скопления) точек.
К основным задачам, связанным с построением модели факторного анализа, относятся задачи существования и идентификации (единственности) модели, статистического оценивания неизвестных параметров и их алгоритмического определения, а также статистической проверки гипотез об адекватности модели наблюдаемым данным, о значениях структурных параметров и т. п.
"8 Мозговой штурм" - тут тоже много полезного для Вас.
Идентификация линейной модели факторного анализа состоит в определении необходимых и достаточных условий, налагаемых на  матрицу факторных нагрузок
матрицу факторных нагрузок  с тем, чтобы при предположении существования решения уравнения (4.2.) относительно матриц структурных параметров
с тем, чтобы при предположении существования решения уравнения (4.2.) относительно матриц структурных параметров  и
и  это решение было единственным с точностью до умножения справа матрицы
это решение было единственным с точностью до умножения справа матрицы  на любую ортогональную матрицу
на любую ортогональную матрицу  порядка
порядка  .
.
Пусть  - последовательность независимых одинаково распределённых случайных векторов, представляющих выборочные данные или выборку. В качестве оценок для
- последовательность независимых одинаково распределённых случайных векторов, представляющих выборочные данные или выборку. В качестве оценок для  и
и  выбирают
выбирают  и
и  соответственно. Процедуру оценивания матриц структурных параметров можно представить как поиск «наилучшей» аппроксимации матрицы
соответственно. Процедуру оценивания матриц структурных параметров можно представить как поиск «наилучшей» аппроксимации матрицы 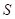 в классе матриц
в классе матриц  , где
, где  -
-  , а
, а  -
-  диагональная матрица переменных, в смысле минимизации некоторой выбранной функции расстояния или функции аппроксимации
диагональная матрица переменных, в смысле минимизации некоторой выбранной функции расстояния или функции аппроксимации  , примерами которых являются
, примерами которых являются  и
и  соответственно. Тогда оценку для
соответственно. Тогда оценку для  по данной
по данной  можно определить как отображение
можно определить как отображение  , удовлетворяющее соотношению
, удовлетворяющее соотношению  , где
, где  - множество
- множество  действительных симметрических положительно определенных матриц;
действительных симметрических положительно определенных матриц;  - множество
- множество  диагональных матриц;
диагональных матриц;  ,
,  - некоторая непрерывная строго вогнутая функция, имеющая непрерывные частные производные до второго порядка включительно, с минимумом в
- некоторая непрерывная строго вогнутая функция, имеющая непрерывные частные производные до второго порядка включительно, с минимумом в  , определённая на спектре обобщённых собственных значений полной проблемы:
, определённая на спектре обобщённых собственных значений полной проблемы:
 ,
,  , (4.3.)
, (4.3.)
где G —  диагональная матрица обобщённых собственных значений с элементами
диагональная матрица обобщённых собственных значений с элементами  , а
, а  - матрица соответствующих обобщённых собственных векторов; k равно наибольшему целому, для которого
- матрица соответствующих обобщённых собственных векторов; k равно наибольшему целому, для которого  . Оценка для
. Оценка для  по данной
по данной  определяется выражением
определяется выражением  , где
, где  -
- диагональная матрица с элементами
диагональная матрица с элементами 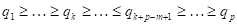
 -
-  матрица соответствующих собственных векторов проблемы (4.3.), где
матрица соответствующих собственных векторов проблемы (4.3.), где  заменяется на
заменяется на  . Тогда при условии только существования
. Тогда при условии только существования  (без предположения о виде распределения
(без предположения о виде распределения  ) и идентифицируемости модели оценки
) и идентифицируемости модели оценки  и
и  строго состоятельны (т. е. при
строго состоятельны (т. е. при  сходятся с вероятностью единица к
сходятся с вероятностью единица к  и
и  соответственно). Таким образом решение задачи оценивания
соответственно). Таким образом решение задачи оценивания  и
и  сводится к оптимизации на собственных значениях обобщённой проблемы (4.3.). Критерием оптимизации является некоторая выбранная функция
сводится к оптимизации на собственных значениях обобщённой проблемы (4.3.). Критерием оптимизации является некоторая выбранная функция  , а переменными —
, а переменными —  диагональных элементов матрицы
диагональных элементов матрицы  . На практике оптимизация осуществляется итеративными методами минимизации функции многих переменных с использованием компьютеров. В предположении
. На практике оптимизация осуществляется итеративными методами минимизации функции многих переменных с использованием компьютеров. В предположении  ~
~ оценки обобщённых наименьших квадратов и максимального правдоподобия для
оценки обобщённых наименьших квадратов и максимального правдоподобия для  есть значения
есть значения  , при которых достигаются минимумы функций
, при которых достигаются минимумы функций  и
и  соответственно. Состоятельные оценки для условного математического ожидания и ковариационной матрицы вектора
соответственно. Состоятельные оценки для условного математического ожидания и ковариационной матрицы вектора  , связанного с отдельным наблюдением
, связанного с отдельным наблюдением  , есть
, есть  и
и  соответственно.
соответственно.
Кроме линейной модели для наблюдаемых количественных переменных (4.1.) в факторном анализе разработаны также линейные модели для порядковых (ранговых) и классификационных (номинальных) показателей. Существуют и нелинейные модели факторного анализа, для которых предложен ряд алгоритмов оценивания параметров. Однако задача идентификации таких моделей теоретически не решена и неизвестны свойства получаемых оценок. Факторный анализ при конкретной реализации связан со значительными затратами времени компьютера из-за громоздкости вычислительных процедур, сложности итерационных процессов и, как правило, больших размеров матрицы исходных данных.
На практике факторный анализ обычно используется, во-первых, как метод свёртки информации с целью понижения пространства наблюдаемых переменных, во-вторых, как метод выделения источников вариации матрицы наблюдений, исключающий вариацию ошибок, и, наконец, как метод классификации многомерных наблюдений. Факторный анализ находит широкое применение в экономических исследованиях, таких как анализ систем экономических показателей, построение обобщающих показателей экономического и социально-экономического развития предприятий, регионов, стран, классификация экономических объектов, анализ спроса и предложения и др.





















