Регрессионный и корреляционный анализ
Власов М. П.
конспект лекций по дисциплине
Компьютерные методы статистического анализа и прогнозирование
ТЕМА 4 Регрессионный и корреляционный анализ
Содержание
стр.
1. Наилучшее приближение и метод наименьших квадратов ……….. 2
2. Регрессионный анализ …..…………………………………………… 8
3. Классическая линейная модель множественной регрессии ……... 16
Рекомендуемые материалы
4. Корреляция и корреляционный анализ ……………………………. 18
5. Автокорреляция …………………………………….……………….. 29
6. Модель авторегрессии ……..……………………………………….. 32
Санкт-Петербург 2008
1. Наилучшее приближение и метод наименьших квадратов
Наилучшее приближение это понятие теории приближения функций. Пусть  — произвольная непрерывная функция, заданная на некотором отрезке
— произвольная непрерывная функция, заданная на некотором отрезке  , a
, a  — фиксированная система непрерывных на том же отрезке функций. Тогда максимум выражения
— фиксированная система непрерывных на том же отрезке функций. Тогда максимум выражения
 (*)
(*)
на отрезке  называется уклонением функции
называется уклонением функции  от полинома
от полинома
 ,
,
а минимум уклонения для всевозможных полиномов  (т.е. при всевозможных наборах коэффициентов
(т.е. при всевозможных наборах коэффициентов  ) — наилучшим приближением функции
) — наилучшим приближением функции  посредством системы
посредством системы  . Наилучшее приближение обозначают через
. Наилучшее приближение обозначают через  . Таким образом, наилучшее приближение является минимумом максимума или, как говорят, минимаксом. Полином
. Таким образом, наилучшее приближение является минимумом максимума или, как говорят, минимаксом. Полином  , для которого уклонение от функции
, для которого уклонение от функции  равно наилучшему приближению (такой полином всегда существует), называется полиномом, наименее уклоняющимся от функции
равно наилучшему приближению (такой полином всегда существует), называется полиномом, наименее уклоняющимся от функции  (на отрезке
(на отрезке  ).
).
Понятия наилучшее приближение и полинома, наименее уклоняющегося от функции  , были впервые введены П. Л. Чебышевым (1854) в связи с исследованиями по теории механизмов. Можно также рассматривать наилучшее приближение, когда под уклонением функции
, были впервые введены П. Л. Чебышевым (1854) в связи с исследованиями по теории механизмов. Можно также рассматривать наилучшее приближение, когда под уклонением функции  от полинома
от полинома  понимается не максимум выражения (*), а, например, выражение
понимается не максимум выражения (*), а, например, выражение
 .
.
Метод наименьших квадратов это один из наиболее распространённых и популярных методов, используемых в практике анализа экспериментальных данных при исследовании зависимостей между различными группами переменных. Основные положения теории разработаны немецким математиком К. Ф. Гауссом (1794 — 95) и французским математиком А. М. Лежандром (1805 — 06). Первоначально метод наименьших квадратов использовался для обработки результатов астрономических и геодезических наблюдений. Строгое математическое обоснование и установление границ содержательной применимости метода наименьших квадратов дано отечественными учёными А. А. Марковым и А. Н. Колмогоровым. Метод наименьших квадратов — один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.
Основная модель, рассматриваемая в рамках метода наименьших квадратов, имеет вид:
 ,
,  , (1.1)
, (1.1)
где  — номер наблюдения,
— номер наблюдения,
 ,- — результат наблюдения при условиях
,- — результат наблюдения при условиях  ,
,
 — неизвестные параметры,
— неизвестные параметры,
 — погрешность наблюдения
— погрешность наблюдения  .
.
Все указанные величины ( ) могут быть векторами или даже более сложными структурами (например, элементами функциональных пространств). В дальнейшем будет предполагаться, что
) могут быть векторами или даже более сложными структурами (например, элементами функциональных пространств). В дальнейшем будет предполагаться, что  ,
,  . Структура
. Структура  — несущественна. Функцию
— несущественна. Функцию  часто называют «функцией отклика» или «откликом».
часто называют «функцией отклика» или «откликом».
Оценками по методу наименьших квадратов называются
 ……………………………..(1.2)
……………………………..(1.2)
 ,
,
где  ,
,  — веса. Обычно
— веса. Обычно  .
.
При рассмотрении метода наименьших квадратов целесообразно разделить вычислительные и статистические аспекты проблемы.
Вычисление оценок по методу наименьших квадратов. Рассмотрим, прежде всего, случай линейной параметризации:  с
с  . Прямые вычисления приводят к следующему результату:
. Прямые вычисления приводят к следующему результату:
 , (1.3.)
, (1.3.)
где  ,
,  .
.
При использовании операции обращения предполагается регулярность соответствующих матриц. В противном случае следует обратиться к псевдообратным матрицам.
Формула (1.2) редко используется в практических расчётах, она более пригодна для теоретических изысканий. В большинстве программ используются алгоритмы, базирующиеся на прямом решении системы линейных уравнений  . Если обозначить через
. Если обозначить через  истинные значения оцениваемых параметров (т.е. удовлетворяющих (1.1), (1.2) при отсутствии ошибок наблюдения), то
истинные значения оцениваемых параметров (т.е. удовлетворяющих (1.1), (1.2) при отсутствии ошибок наблюдения), то
 (1.4)
(1.4)
Изучение поведения остаточного члена при различных вероятностных предположениях об ошибках  составляет предмет статистического анализа свойств оценок по методу наименьших квадратов. Очевидно, что (1.4) может анализироваться и в рамках детерминистического подхода. Например, предположение о том, что
составляет предмет статистического анализа свойств оценок по методу наименьших квадратов. Очевидно, что (1.4) может анализироваться и в рамках детерминистического подхода. Например, предположение о том, что
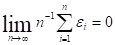
при довольно слабых ограничениях на положения точек  , (план эксперимента) и вид функции
, (план эксперимента) и вид функции  приведёт к тому, что
приведёт к тому, что  .
.
В тех случаях, когда  определяется линейными ограничениями
определяется линейными ограничениями  , решением оптимизационной задачи (1.1) является:
, решением оптимизационной задачи (1.1) является:
 . (1.5)
. (1.5)
В вычислительной практике  чаще находится как решение линейной системы
чаще находится как решение линейной системы  ,
,  .
.
При нелинейной параметризации оптимизационная задача (1.1) оказывается весьма трудной для многих используемых на практике функций отклика. Сумма квадратичных отклонений  может иметь несколько локальных минимумов. Неудачное расположение точек
может иметь несколько локальных минимумов. Неудачное расположение точек  приводит к плохой обусловленности оптимизационной задачи. В линейном случае для преодоления этой трудности разработаны довольно мощные методы регуляризации. При нелинейной — регуляризация осуществляется обычно на «интуитивном уровне». Помимо формальной (вычислительной) регуляризации необходимо помнить об оптимизации расположения точек
приводит к плохой обусловленности оптимизационной задачи. В линейном случае для преодоления этой трудности разработаны довольно мощные методы регуляризации. При нелинейной — регуляризация осуществляется обычно на «интуитивном уровне». Помимо формальной (вычислительной) регуляризации необходимо помнить об оптимизации расположения точек  , т. е. планировании эксперимента. Для многих эконометрических задач плохая обусловленность заложена в самих функциях отклика (примеры: логистические кривые, переусложнённые производственные функции).
, т. е. планировании эксперимента. Для многих эконометрических задач плохая обусловленность заложена в самих функциях отклика (примеры: логистические кривые, переусложнённые производственные функции).
Для поиска оценок по методу наименьших квадратов могут использоваться любые стандартные методы оптимизации, однако в большинстве статистических пакетов предпочтение отдаётся методам, использующим квадратичную структуру  и отчасти опирающимся на процедуры, развитыми для линейного случая.
и отчасти опирающимся на процедуры, развитыми для линейного случая.
Наиболее распространёнными являются различные модификации метода Гаусса — Ньютона. Все они опираются на идею линеаризации отклика в пространстве параметров  с последующим использованием аналогов (1.2) или (1.4). Большинство из них вписывается в следующую итерационную схему:
с последующим использованием аналогов (1.2) или (1.4). Большинство из них вписывается в следующую итерационную схему:
 , (1.6)
, (1.6)
где
 ,
,
 ,
,
 ,
,  .
.
Ha (1.6) ссылаются как на метод Хартли. При использовании вместо  матрицы
матрицы  ,
,  процедуру (1.6) называют методом Марквардта. Во многие статистические пакеты включены методы, в которых при каждом заданном
процедуру (1.6) называют методом Марквардта. Во многие статистические пакеты включены методы, в которых при каждом заданном  в пространстве параметров функция отклика аппроксимируется плоскостью с помощью метода наименьших квадратов. Подобный приём избавляет пользователя от программирования производных
в пространстве параметров функция отклика аппроксимируется плоскостью с помощью метода наименьших квадратов. Подобный приём избавляет пользователя от программирования производных  , сохраняя эффективность используемых алгоритмов.
, сохраняя эффективность используемых алгоритмов.
Статистические свойства оценок по методу наименьших квадратов. В большинстве исследований, связанных с методом наименьших квадратов, исходная модель дополняется следующим принципиальным предположением: ошибки наблюдений  являются случайными величинами. Для получения конструктивных результатов это предположение детализируется. Например, обуславливается, что
являются случайными величинами. Для получения конструктивных результатов это предположение детализируется. Например, обуславливается, что  имеют нулевые средние и известные дисперсии, распределены в соответствии с нормальным законом или нормальным законом о «с примесями», независимы в совокупности и т. д. Изложим кратко свойства оценок по методу наименьших квадратов при некоторых стандартных предположениях с постепенной их детализацией.
имеют нулевые средние и известные дисперсии, распределены в соответствии с нормальным законом или нормальным законом о «с примесями», независимы в совокупности и т. д. Изложим кратко свойства оценок по методу наименьших квадратов при некоторых стандартных предположениях с постепенной их детализацией.
Пусть
(а)  ,
,  ,
,  ,
,  .
.
Справедливы следующие утверждения:
1. Оценки по методу наименьших квадратов - несмещённые, т.е.  , и состоятельные, т. е.
, и состоятельные, т. е.  , если
, если  , где
, где  — положительно определённая матрица.
— положительно определённая матрица.
— Оценки по методу наименьших квадратов имеют наименьшую дисперсионную матрицу (в частности наименьшие дисперсии) среди всех линейных несмещённых оценок, если  .
.
— Дисперсионная матрица оценок  вычисляется по формуле
вычисляется по формуле  , дисперсия оценки функции отклика в заданной точке
, дисперсия оценки функции отклика в заданной точке  равна
равна
 .
.
2. При линейных ограничениях
 .
.
Преобразование  ,
,  приводит исходную модель к модели с равноточными наблюдениями. Если дисперсия ошибок наблюдении неизвестна, то её оценкой может служить
приводит исходную модель к модели с равноточными наблюдениями. Если дисперсия ошибок наблюдении неизвестна, то её оценкой может служить  , соответственно,
, соответственно,
 ,
,  .
.
Предположим дополнительно к (а), что случайные величины  распределены по нормальному закону. Тогда справедливы следующие утверждения:
распределены по нормальному закону. Тогда справедливы следующие утверждения:
— При известной дисперсии погрешности наблюдений оценки по методу наименьших квадратов оценки распределены по нормальному закону, со средними  и с дисперсионной матрицей
и с дисперсионной матрицей  .
.
— При  случайная величина
случайная величина
 ,
,  ,
,
имеет  — распределение (распределение Фишера). Данный факт позволяет реализовать проверку гипотез описываемых системой линейных уравнений.
— распределение (распределение Фишера). Данный факт позволяет реализовать проверку гипотез описываемых системой линейных уравнений.
— Случайная величина
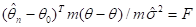
имеет  — распределение. Решая неравенство
— распределение. Решая неравенство  , подсчитывают доверительный эллипсоид для
, подсчитывают доверительный эллипсоид для  , т. е. эллипсоид, накрывающий с вероятностью
, т. е. эллипсоид, накрывающий с вероятностью  истинное значение искомых параметров.
истинное значение искомых параметров.
При нелинейной по параметрам функции отклика все утверждения данного раздела носят асимптотический характер, т. е. они приближённо выполняются при достаточно большом числе наблюдений  и приближение тем лучше, чем больше
и приближение тем лучше, чем больше  .
.
2. Регрессионный анализ
Регрессия (от лат. regressio — движение назад) это зависимость условного среднего значения результирующего показателя  , вычисленного при условии, что величины предсказывающих переменных зафиксированы на уровнях
, вычисленного при условии, что величины предсказывающих переменных зафиксированы на уровнях  от заданных значений объясняющих переменных. Функция
от заданных значений объясняющих переменных. Функция  , описывающая эту зависимость, называется функцией регрессии.
, описывающая эту зависимость, называется функцией регрессии.
Пусть значения исследуемого результирующего показателя  при данных фиксированных величинах объясняющих переменных
при данных фиксированных величинах объясняющих переменных 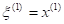
 случайным образом флюктуируют вокруг некоторого уровня
случайным образом флюктуируют вокруг некоторого уровня  , т.е.
, т.е.
 ,
,
где остаточная компонента  определяет случайное отклонение значения
определяет случайное отклонение значения  от постоянного (при фиксированных
от постоянного (при фиксированных  ) уровня
) уровня  . При этом наличие флюктуации
. При этом наличие флюктуации  может быть присуще самой природе эксперимента или наблюдения, а может объясняться случайными ошибками в измерении величины
может быть присуще самой природе эксперимента или наблюдения, а может объясняться случайными ошибками в измерении величины  . Как правило, предполагается, что среднее значение зависящих от конкретных значений
. Как правило, предполагается, что среднее значение зависящих от конкретных значений  флюктуации равно нулю, поэтому
флюктуации равно нулю, поэтому
 .
.
В качестве примера одномерной функции  , возникающей в экономико-математическом моделировании, укажем
, возникающей в экономико-математическом моделировании, укажем  , где
, где  , (руб.) — среднедушевой доход и
, (руб.) — среднедушевой доход и  (руб.) — среднедушевые денежные сбережения в семье, случайно извлечённой из рассматриваемой совокупности семей, однородной по своему потребительскому поведению.
(руб.) — среднедушевые денежные сбережения в семье, случайно извлечённой из рассматриваемой совокупности семей, однородной по своему потребительскому поведению.
Регрессионный анализ является разделом математической статистики, объединяющим практические методы исследования регрессионной зависимости между величинами по статистическим данным. Проблема регрессии в математической статистике характерна тем, что о распределениях изучаемых величин нет достаточной информации. Пусть, например, имеются основания предполагать, что случайная величина  имеет некоторое распределение вероятностей при фиксированных значениях
имеет некоторое распределение вероятностей при фиксированных значениях  других величин и случайным образом флюктуирует вокруг некоторого (вообще говоря, неизвестного) условного среднего
других величин и случайным образом флюктуирует вокруг некоторого (вообще говоря, неизвестного) условного среднего  . Следует отметить две разные ситуации. В зависимости от природы задачи и целей статистического анализа результаты эксперимента интерпретируют по-разному в отношении предсказывающих переменных
. Следует отметить две разные ситуации. В зависимости от природы задачи и целей статистического анализа результаты эксперимента интерпретируют по-разному в отношении предсказывающих переменных  . В первом случае величины
. В первом случае величины  являются контролируемыми величинами, и их значения заранее задаются (планируются) при проведении эксперимента. Во втором случае переменные
являются контролируемыми величинами, и их значения заранее задаются (планируются) при проведении эксперимента. Во втором случае переменные  являются неконтролируемыми и мы располагаем выборкой (
являются неконтролируемыми и мы располагаем выборкой (
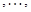
 из некоторой
из некоторой  -мерной совокупности (здесь верхний индекс в скобках относится к номеру наблюдения).
-мерной совокупности (здесь верхний индекс в скобках относится к номеру наблюдения).
Проведение регрессионного анализа можно условно разбить на четыре этапа:
· параметризация модели;
· анализ мультиколлинеарности и отбор наиболее информативных факторов;
· вычисление оценок неизвестных параметров, входящих в исследуемое уравнение статистической связи;
· анализ точности полученных уравнений связи.
Главная цель исследований на первом этапе — определение общего вида, структуры искомой связи между  и
и  , другими словами, описание класса функций
, другими словами, описание класса функций  , которому, как будем в дальнейшем предполагать, принадлежит функция
, которому, как будем в дальнейшем предполагать, принадлежит функция  . Чаще всего это описание даётся в форме некоторого конечно параметрического семейства функций
. Чаще всего это описание даётся в форме некоторого конечно параметрического семейства функций  ,
,  , поэтому этот этап называется также этапом параметризации модели. Являясь решающим звеном во всём процессе статистического исследования зависимостей, этот этап находится в наименее выгодном положении по сравнению с другими этапами (с позиций наличия строгих математических рекомендаций по его реализации). Поэтому его реализация требует совместной работы специалиста соответствующей предметной области и математика-статистика. Существует подход к исследованию моделей регрессии, не требующий предварительного выбора конечно параметрического семейства
, поэтому этот этап называется также этапом параметризации модели. Являясь решающим звеном во всём процессе статистического исследования зависимостей, этот этап находится в наименее выгодном положении по сравнению с другими этапами (с позиций наличия строгих математических рекомендаций по его реализации). Поэтому его реализация требует совместной работы специалиста соответствующей предметной области и математика-статистика. Существует подход к исследованию моделей регрессии, не требующий предварительного выбора конечно параметрического семейства  , в рамках которого проводится дальнейший анализ. Речь идёт о так называемых непараметрических (или семипараметрических) методах исследования регрессионных зависимостей. Возникающие здесь проблемы (необходимость иметь большие объёмы исходных статистических данных, выбор параметров сглаживания и «окон», выбор порядка сплайна, числа и положения «узлов» и т.п.) сопоставимы по своей сложности с проблемами, возникающими для параметрических моделей.
, в рамках которого проводится дальнейший анализ. Речь идёт о так называемых непараметрических (или семипараметрических) методах исследования регрессионных зависимостей. Возникающие здесь проблемы (необходимость иметь большие объёмы исходных статистических данных, выбор параметров сглаживания и «окон», выбор порядка сплайна, числа и положения «узлов» и т.п.) сопоставимы по своей сложности с проблемами, возникающими для параметрических моделей.
Под явлением мультиколлинеарности в регрессионном анализе понимается наличие тесных статистических связей между предсказывающими переменными  . Эффект мультиколлинеарности влечёт крайнюю неустойчивость получаемых числовых характеристик анализируемых моделей и затрудняет содержательную интерпретацию параметров этих моделей. Поэтому исследователь стремится перейти к такой новой системе предсказывающих переменных, в которой эффект мультиколлинеарности уже не имел бы места.
. Эффект мультиколлинеарности влечёт крайнюю неустойчивость получаемых числовых характеристик анализируемых моделей и затрудняет содержательную интерпретацию параметров этих моделей. Поэтому исследователь стремится перейти к такой новой системе предсказывающих переменных, в которой эффект мультиколлинеарности уже не имел бы места.
На третьем этапе исследования, после того как выбран класс  допустимых функций, решают задачу минимизации
допустимых функций, решают задачу минимизации
 ,
,
где функционал  задаёт критерии качества аппроксимации результирующего показателя
задаёт критерии качества аппроксимации результирующего показателя  с помощью функции
с помощью функции  из класса
из класса  . Обычно функционал
. Обычно функционал  строится в виде некоторой функции от невязок
строится в виде некоторой функции от невязок  , например, в виде
, например, в виде
 ,
,
где  — функция потерь, выбираемая, как правило, монотонно неубывающей, выпуклой, с неотрицательными значениями. Приведём ряд частных случаев функции потерь
— функция потерь, выбираемая, как правило, монотонно неубывающей, выпуклой, с неотрицательными значениями. Приведём ряд частных случаев функции потерь  , широко используемых в теории и практике статистического исследования зависимостей:
, широко используемых в теории и практике статистического исследования зависимостей:
1)  ; получаемая регрессия называется среднеквадратической, а метод, реализующий минимизацию функционала
; получаемая регрессия называется среднеквадратической, а метод, реализующий минимизацию функционала  , принято называть методом наименьших квадратов.
, принято называть методом наименьших квадратов.
2)  ; получаемая регрессия называется медианной регрессией, а метод, реализующий минимизацию функционала
; получаемая регрессия называется медианной регрессией, а метод, реализующий минимизацию функционала  , называют в этом случае методом наименьших модулей.
, называют в этом случае методом наименьших модулей.
3) Минимизация по  величины
величины  приводит к минимаксной регрессии.
приводит к минимаксной регрессии.
Найденная аппроксимация  неизвестной теоретической функции
неизвестной теоретической функции  (называемая эмпирической функцией регрессии) является лишь некоторым приближением истинной зависимости
(называемая эмпирической функцией регрессии) является лишь некоторым приближением истинной зависимости  . При этом погрешность
. При этом погрешность  в описании неизвестной истинной функции
в описании неизвестной истинной функции  с помощью
с помощью  в общем случае состоит из двух составляющих: ошибки аппроксимации
в общем случае состоит из двух составляющих: ошибки аппроксимации  и ошибки выборки
и ошибки выборки  . Величина
. Величина  зависит от успеха в реализации первого этапа, т.е. от правильности выбора класса допустимых решений
зависит от успеха в реализации первого этапа, т.е. от правильности выбора класса допустимых решений  . В частности, если класс
. В частности, если класс  выбран таким образом, что включает в себя и неизвестную истинную функцию
выбран таким образом, что включает в себя и неизвестную истинную функцию  (т.е.
(т.е.  ), то ошибка аппроксимации
), то ошибка аппроксимации  =0. Но даже в этом случае остаётся случайная составляющая (ошибка выборки)
=0. Но даже в этом случае остаётся случайная составляющая (ошибка выборки)  , обусловленная ограниченностью выборочных данных, на основании которых подбирается функция
, обусловленная ограниченностью выборочных данных, на основании которых подбирается функция  (оцениваются её параметры). Уменьшить ошибку выборки можно за счёт увеличения объёма
(оцениваются её параметры). Уменьшить ошибку выборки можно за счёт увеличения объёма  обрабатываемых выборочных данных, т.к. при
обрабатываемых выборочных данных, т.к. при  (т.е. при
(т.е. при  =0) и правильно выбранных методах статистического оценивания (т.е. при правильном выборе оптимизируемого функционала качества модели
=0) и правильно выбранных методах статистического оценивания (т.е. при правильном выборе оптимизируемого функционала качества модели  ошибка выборки
ошибка выборки  (по вероятности) при
(по вероятности) при  (свойство состоятельности используемой процедуры статистического оценивания неизвестной функции
(свойство состоятельности используемой процедуры статистического оценивания неизвестной функции  ).
).
Соответственно на данном этапе приходится решать следующие основные задачи анализа точности полученной регрессионной зависимости:
1) В случае  ,
,  и
и  , т.е. когда класс допустимых решении задаётся параметрическим семейством функций и включает в себя неизвестную теоретическую функцию регрессии
, т.е. когда класс допустимых решении задаётся параметрическим семейством функций и включает в себя неизвестную теоретическую функцию регрессии  , при заданных доверительной вероятности
, при заданных доверительной вероятности  и объёме выборки
и объёме выборки  для любой компоненты неизвестного векторного параметра
для любой компоненты неизвестного векторного параметра  указать такую предельную (гарантированную) величину погрешности
указать такую предельную (гарантированную) величину погрешности  , что
, что  , с вероятностью, не меньшей, чем
, с вероятностью, не меньшей, чем  (здесь
(здесь  — истинное значение компоненты
— истинное значение компоненты  неизвестного параметра
неизвестного параметра  , a
, a  — его статистическая оценка).
— его статистическая оценка).
2) При заданных доверительной вероятности  , объёме выборки
, объёме выборки  и значениях предсказывающих (объясняющих) переменных
и значениях предсказывающих (объясняющих) переменных  указать такую гарантированную величину погрешности
указать такую гарантированную величину погрешности  , что
, что  , где
, где  — эмпирическая функция регрессии.
— эмпирическая функция регрессии.
3) При заданных доверительной вероятности  , объёме выборки
, объёме выборки  и значениях предсказывающих переменных
и значениях предсказывающих переменных  указать такую гарантированную величину погрешности
указать такую гарантированную величину погрешности  , что
, что  с вероятностью, не меньшей, чем
с вероятностью, не меньшей, чем  (здесь
(здесь  — прогнозируемое индивидуальное значение исследуемого результирующего показателя при значениях объясняющих переменных, равных
— прогнозируемое индивидуальное значение исследуемого результирующего показателя при значениях объясняющих переменных, равных  ).
).
Приведём примеры наиболее распространённых на практике моделей регрессии. Общая форма модели имеет вид
 ,
,  ,
,
где величины  характеризуют случайные ошибки, которые будем предполагать независимыми при различных измерениях и одинаково распределёнными с нулевым средним и постоянной дисперсией,
характеризуют случайные ошибки, которые будем предполагать независимыми при различных измерениях и одинаково распределёнными с нулевым средним и постоянной дисперсией,  — вектор неизвестных параметров. Наиболее естественной с точки зрения единого метода оценки неизвестных параметров является модель регрессии, линейная относительно этих параметров:
— вектор неизвестных параметров. Наиболее естественной с точки зрения единого метода оценки неизвестных параметров является модель регрессии, линейная относительно этих параметров:
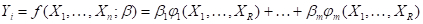
Наиболее важное значение имеет случай, когда  — ортогональные многочлены соответствующих порядков, построенные по распределению
— ортогональные многочлены соответствующих порядков, построенные по распределению  .
.
Другими примерами являются случаи тригонометрической регрессии, показательной регрессии и т.п. Самой распространённой является линейная модель регрессии, которая в матричном виде записывается следующим образом:
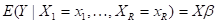
 ,
,
где  — вектор коэффициентов регрессии,
— вектор коэффициентов регрессии,  ,
,  ,
,  =, — матрица известных величин, связанных друг с другом, вообще говоря, произвольным образом,
=, — матрица известных величин, связанных друг с другом, вообще говоря, произвольным образом,  — единичная матрица порядка
— единичная матрица порядка  ; при этом
; при этом  и
и  . В более общем случае допускается корреляция между наблюдениями
. В более общем случае допускается корреляция между наблюдениями  :
:
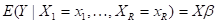 ,
,
 ,
,
где матрица  известна. Эта схема, однако, сводится к предыдущей. Несмещённой оценкой
известна. Эта схема, однако, сводится к предыдущей. Несмещённой оценкой  по методу наименьших квадратов является величина
по методу наименьших квадратов является величина
 ,
,  ,
,
а несмещённой оценкой для  служит
служит
 .
.
Указанный метод построения эмпирической регрессии в предположении нормального распределения результатов наблюдений приводит к оценкам для  и
и  , совпадающим с оценками наибольшего правдоподобия. Однако оценки, полученные этим методом, остаются в некотором смысле наилучшими и в случае отклонения от нормальности, если только объём выборки достаточно велик.
, совпадающим с оценками наибольшего правдоподобия. Однако оценки, полученные этим методом, остаются в некотором смысле наилучшими и в случае отклонения от нормальности, если только объём выборки достаточно велик.
В данной матричной форме общая линейная модель регрессии допускает естественное обобщение на случай, когда наблюдаемые величины  являются векторными величинами. При этом не возникает никаких дополнительных трудностей.
являются векторными величинами. При этом не возникает никаких дополнительных трудностей.
Задача анализа точности построенной регрессионной зависимости для линейной модели наиболее эффективно решается при допущении, что вектор наблюдений  распределён нормально. В этом случае можно показать, что статистика
распределён нормально. В этом случае можно показать, что статистика
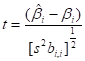
подчиняется распределению Стьюдента с  степенями свободы. Этот факт используется для построения доверительных интервалов для параметров
степенями свободы. Этот факт используется для построения доверительных интервалов для параметров  и для проверки гипотез о значениях, которые принимает величина
и для проверки гипотез о значениях, которые принимает величина  . Помимо этого можно найти доверительные интервалы для
. Помимо этого можно найти доверительные интервалы для  при фиксированных значениях всех регрессионных переменных и доверительные интервалы, содержащие следующее (
при фиксированных значениях всех регрессионных переменных и доверительные интервалы, содержащие следующее ( -ое значение величины
-ое значение величины  (так называемые интервалы предсказания). Наконец, можно на основе вектора выборочных коэффициентов регрессии
(так называемые интервалы предсказания). Наконец, можно на основе вектора выборочных коэффициентов регрессии  построить доверительный эллипсоид для вектора
построить доверительный эллипсоид для вектора  или для любой совокупности неизвестных коэффициентов регрессии, а также доверительную область для всей линии или прямой регрессии.
или для любой совокупности неизвестных коэффициентов регрессии, а также доверительную область для всей линии или прямой регрессии.
Предположим, что элементы матрицы  в линейной модели нормированы так, что ХТХ — корреляционная матрица. Если собственные числа
в линейной модели нормированы так, что ХТХ — корреляционная матрица. Если собственные числа  матрицы ХТХ положительны, но среди них имеются близкие к нулю, то обычная оценка наименьших квадратов
матрицы ХТХ положительны, но среди них имеются близкие к нулю, то обычная оценка наименьших квадратов  обладает рядом недостатков. Во-первых, средний квадрат евклидова расстояния
обладает рядом недостатков. Во-первых, средний квадрат евклидова расстояния  от
от  оказывается весьма большим, то же относится и к квадрату нормы вектора
оказывается весьма большим, то же относится и к квадрату нормы вектора  (исследователи, работающие с плохо обусловленными матрицами ХТХ, часто сталкиваются с очень большими по модулю значениями оценок
(исследователи, работающие с плохо обусловленными матрицами ХТХ, часто сталкиваются с очень большими по модулю значениями оценок  ). Во-вторых, знаки компонент
). Во-вторых, знаки компонент  могут меняться при малом изменении матрицы X. Один из подходов в такой ситуации состоит в том, чтобы строить такие линейные оценки, которые являлись бы немного смещёнными, но зато уменьшали бы средний квадрат ошибки по сравнению с
могут меняться при малом изменении матрицы X. Один из подходов в такой ситуации состоит в том, чтобы строить такие линейные оценки, которые являлись бы немного смещёнными, но зато уменьшали бы средний квадрат ошибки по сравнению с  . Соответствующий метод получил название гребневой регрессии.
. Соответствующий метод получил название гребневой регрессии.
В случае, когда функция  нелинейно зависит от вектора параметров
нелинейно зависит от вектора параметров  , нахождение оценок наименьших квадратов сводится к решению следующей экстремальной задачи:
, нахождение оценок наименьших квадратов сводится к решению следующей экстремальной задачи:
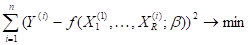
Известно большое число итеративных процедур минимизации этого квадратичного функционала (метод градиентного спуска, метод Гаусса-Ньютона, алгоритм Марквардта, DUD-метод и др.).
В 1980-х гг. в анализе регрессионных зависимостей стали популярными задачи робастного (устойчивого) оценивания, задачи оценивания при наличии ошибок в предсказывающих переменных, расширился арсенал непараметрическнх методов оценивания регрессий, методы регрессионного анализа стали применяться для переменных смешанного типа.
Регрессионный анализ является самым распространённым методом обработки экспериментальных данных при изучении зависимостей в экономике, физике, биологии, экономике, медицине и др. областях. На моделях регрессионного анализа основаны такие разделы математической статистики, как дисперсионный анализ и планирование эксперимента.
3. Классическая линейная модель множественной регрессии
Общее уравнение регрессионной зависимости результирующей переменной  от объясняющих переменных (предикторов)
от объясняющих переменных (предикторов)  при аддитивно наложенных регрессионных остатках
при аддитивно наложенных регрессионных остатках  (
( ) имеет вид
) имеет вид
 , (3.1)
, (3.1)
где  — функция регрессии
— функция регрессии  по
по  . Присутствие случайной остаточной составляющей (регрессионных остатков)
. Присутствие случайной остаточной составляющей (регрессионных остатков)  в уравнении (3.1.) обусловлено причинами двоякой природы: во-первых, она отражает влияние на формирование значений
в уравнении (3.1.) обусловлено причинами двоякой природы: во-первых, она отражает влияние на формирование значений  факторов, не учтённых в перечне объясняющих переменных.
факторов, не учтённых в перечне объясняющих переменных.  ; во-вторых, она может включать в себя случайную погрешность измерений значений результирующей переменной
; во-вторых, она может включать в себя случайную погрешность измерений значений результирующей переменной  . Из определения функции
. Из определения функции  непосредственно следует, что при любых фиксированных значениях
непосредственно следует, что при любых фиксированных значениях 
 , (3.2.)
, (3.2.)
а функция регрессии  является функцией неслучайной.
является функцией неслучайной.
Способ статистического анализа моделей типа (3.1) — (3.2) по результатам  измерений анализируемых переменных
измерений анализируемых переменных  , —
, —  зависит от конкретизации требований к виду функции
зависит от конкретизации требований к виду функции  , природе объясняющих переменных
, природе объясняющих переменных  и случайных регрессионных остатков
и случайных регрессионных остатков  . Классическая линейная модель множественной регрессии представляет собой простейшую версию такой конкретизации, а именно:
. Классическая линейная модель множественной регрессии представляет собой простейшую версию такой конкретизации, а именно:
( ) функция регрессии
) функция регрессии  линейна по объясняющим переменным
линейна по объясняющим переменным  , т.е.
, т.е.
 ………….. (3.3.)
………….. (3.3.)
(среди переменных  может присутствовать переменная, тождественно равная единице; тогда уравнение (3.3) будет содержать свободный член);
может присутствовать переменная, тождественно равная единице; тогда уравнение (3.3) будет содержать свободный член);
(ii) дисперсия регрессионных остатков не зависит от того, при каких значениях объясняющих переменных производятся наблюдения, т. е.
 , (3.4)
, (3.4)
а сами регрессионные остатки, соответствующие различным наблюдениям, взаимно некоррелированы, т. е.
 при
при  ; (3.5.)
; (3.5.)
регрессионные остатки, удовлетворяющие условию (3.4), называются гомоскедастичными, а само свойство независимости дисперсии от характеристик условий наблюдения — гомоскедастичностью;
( ) объясняющие переменные
) объясняющие переменные  не являются случайными величинами, т. е. представляют собой некоторые неслучайные характеристики условий проведения наблюдений (регистрации) значений анализируемых переменных
не являются случайными величинами, т. е. представляют собой некоторые неслучайные характеристики условий проведения наблюдений (регистрации) значений анализируемых переменных  и
и  .
.
С учётом (3.1.) — (3.5.) классическая линейная модель множественной регрессии в терминах исходных наблюдений  может быть представлена (в матричной форме) в виде:
может быть представлена (в матричной форме) в виде:
 ,
,
где
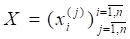
 - матрица наблюдённых значений объясняющих переменных,
- матрица наблюдённых значений объясняющих переменных,
 — вектор-столбец наблюдённых значений результирующей (зависимой) переменной,
— вектор-столбец наблюдённых значений результирующей (зависимой) переменной,
 — вектор-столбец неизвестных коэффициентов регрессии,
— вектор-столбец неизвестных коэффициентов регрессии,
 — вектор-столбец регрессионных остатков,
— вектор-столбец регрессионных остатков,
0 — вектор-столбец, состоящий из  нулей,
нулей,
 — ковариационная матрица вектора регрессионных остатков,
— ковариационная матрица вектора регрессионных остатков,
 — единичная матрица.
— единичная матрица.
Если к условиям (0 — (iii) добавляют условие нормальной распределённости регрессионных остатков  , то соответствующую регрессионную модель называют классической нормальной.
, то соответствующую регрессионную модель называют классической нормальной.
В некоторых работах условие (iii) ослаблено: допускается случайный характер объясняющих переменных, но требуется, чтобы объясняющие переменные были некоррелированы с регрессионными остатками  .
.
4.Корреляция и корреляционный анализ
Корреляция это величина, характеризующая взаимную зависимость двух случайных величин  и
и  — безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Пусть, например,
— безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Пусть, например,  — затраты на рекламу, а
— затраты на рекламу, а  — объём продаж. Величина
— объём продаж. Величина
 ,
,
где  — математическое ожидание, называется корреляционной функцией или ковариацией
— математическое ожидание, называется корреляционной функцией или ковариацией  и
и  . Если объём продаж не зависит от рекламы, то ковариация
. Если объём продаж не зависит от рекламы, то ковариация  и
и  равна нулю. Чем лучше зависимость описывается линейной функцией:
равна нулю. Чем лучше зависимость описывается линейной функцией:  , где
, где  и
и  — некоторые числа, тем больше абсолютная величина
— некоторые числа, тем больше абсолютная величина  .
.
Для того, чтобы характеристика связи не зависела от единиц, в которых измерены исследуемые признаки, и менялась в постоянных пределах, используется коэффициент корреляции:
 ,
,
где  и
и  — стандартные отклонения
— стандартные отклонения  и
и  соответственно. Помимо того, что
соответственно. Помимо того, что  в случае независимости, эта величина принимает значения +1 и -1 соответственно при положительной и отрицательной линейной связи. При нелинейной зависимости аналогичный показатель называется индексом корреляции. Коэффициент корреляции служит для измерения тесноты статистической связи между двумя случайными величинами.
в случае независимости, эта величина принимает значения +1 и -1 соответственно при положительной и отрицательной линейной связи. При нелинейной зависимости аналогичный показатель называется индексом корреляции. Коэффициент корреляции служит для измерения тесноты статистической связи между двумя случайными величинами.
Если имеются данные об объёмах продаж и затратах на рекламу в  районах:
районах:  и
и  ,
,  , то коэффициент корреляции между ними можно оценить с помощью формулы
, то коэффициент корреляции между ними можно оценить с помощью формулы
 ,
,
где
 ,
,  ;
;
 ;
; 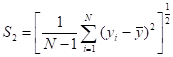
— оценки математических ожиданий и стандартных отклонений.
Как правило, близость  к + 1 или - 1 говорит о линейной связи. Часто анализ парных коэффициентов служит прелюдией к применению более сложных методов. Однако всегда следует иметь в виду следующие соображения.
к + 1 или - 1 говорит о линейной связи. Часто анализ парных коэффициентов служит прелюдией к применению более сложных методов. Однако всегда следует иметь в виду следующие соображения.
Оценка коэффициента корреляции может оказаться большой ещё по двум причинам, например:
· объём продаж и реклама тесно связаны с третьим признаком, например с наличием филиалов или представительств в районе.
· число наблюдений недостаточно, чтобы исключить случайное совпадение изменений  и
и  .
.
Эта опасность особенно велика при оценке коэффициента корреляции для нескольких пар признаков. В первом случае рекомендуется пользоваться частными коэффициентами корреляции, а во втором — следить за дисперсией оценок.
Коэффициент корреляции симметричен и не несёт никакой информации о причинности связи.
Если большие значения  свидетельствуют о наличии связи, то близость этой величины к нулю говорит лишь об отсутствии линейной зависимости. Только при совместном нормальном распределении
свидетельствуют о наличии связи, то близость этой величины к нулю говорит лишь об отсутствии линейной зависимости. Только при совместном нормальном распределении  и
и  из
из  делается вывод о независимости. Для проверки такой гипотезы можно пользоваться, например, статистикой
делается вывод о независимости. Для проверки такой гипотезы можно пользоваться, например, статистикой  , которая имеет распределение Стьюдента с
, которая имеет распределение Стьюдента с  степенями свободы.
степенями свободы.
Корреляционный анализ представляет совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между случайными величинами или признаками. Корреляционный анализ — один из ранних этапов (и одновременно разделов) процесса применения специального математико-статистического инструментария, называемого статистическим исследованием зависимостей; он посвящен:
· выбору (с учётом специфики и природы анализируемых признаков  ) подходящих измерителей статистической связи между этими признаками;
) подходящих измерителей статистической связи между этими признаками;
· оценке числовых значений подобранных измерителей по имеющимся исходным статистическим данным  ,
,  (здесь
(здесь  — номер статистически обследованного объекта);
— номер статистически обследованного объекта);
· проверке гипотез о том, что полученные оценочные значения анализируемых измерителей связи действительно свидетельствуют о наличии статистической зависимости между исследуемыми признаками (переменными  );
);
· анализу структуры взаимозависимости исследуемых переменных, результаты которого часто представляются в виде соответствующих графов (сами переменные играют роль узлов такого графа, а соединяющие их отрезки свидетельствуют о наличии статистической связи между данной парой переменных).
При этом в корреляционном анализе речь не идёт о выявлении формы (конкретного вида) исследуемых зависимостей (это - относится к целям и компетенции другого раздела статистического исследования зависимостей — регрессионного анализа), но лишь об установлении самого факта статистической связи и об измерении степени её тесноты.
В качестве основных измерителей степени тесноты связей между количественными переменными в практике статистических исследований используются: индекс корреляции, корреляционное отношение, парные, частные и множественные коэффициенты корреляции, коэффициент детерминации.
Парные корреляционные характеристики позволяют измерять степень тесноты статистической связи между парой переменных без учёта опосредованного или совместного влияния других показателей. Вычисляются (оцениваются) они по результатам наблюдений только анализируемой пары показателей.
Факт установления тесной статистической связи между переменными не является, вообще говоря, достаточным основанием для доказательства существования причинно-следственной связи между этими переменными.
Парные и частные коэффициенты корреляции являются измерителями степени тесноты линейной связи между переменными. В этом случае корреляционные характеристики могут оказаться как положительными, так и отрицательными в зависимости от одинаковой или противоположной тенденции взаимосвязанного изменения анализируемых переменных. При положительных значениях коэффициента корреляции говорят о наличии положительной линейной статистической связи, при отрицательных — об отрицательной.
При наложении случайных ошибок на значения исследуемой пары переменных (например, ошибок измерения) оценка статистической связи между исходными переменными, построенная по наблюдениям, оказывается искажённой. В частности, получаемые при этом оценки коэффициентов корреляции будут заниженными.
Измерителем степени тесноты связи любой формы является корреляционное отношение, для вычисления которого необходимо разбить область значений предсказывающей переменной на интервалы (гиперпараллелепипеды) группирования. Возможна параметрическая модификация корреляционного отношения, при которой вычисление соответствующих выборочных значений не требует предварительного разбиения на интервалы группирования.
Частный коэффициент корреляции позволяет оценить степень тесноты линейной связи между двумя переменными, очищенной от опосредованного влияния других факторов. Для его расчёта необходима исходная информация как по анализируемой паре переменных, так и по всем тем переменным, опосредованное («мешающее») влияние которых нужно элиминировать.
Множественный (совокупный) коэффициент корреляции измеряет степень тесноты статистической связи (любой формы) между некоторым (результирующим) показателем, с одной стороны, и совокупностью других (объясняющих) переменных — с другой. Формально он определён для любой многомерной системы наблюдений. Квадрат его величины (называемый коэффициентом детерминации) показывает, какая доля дисперсии исследуемого результирующего показателя определяется (детерминируется) совокупным влиянием контролируемых нами (в виде функции регрессии) объясняющих переменных. Оставшаяся «необъяснённой» доля дисперсии результирующего показателя определяет ту верхнюю границу точности, которой можно добиться при восстановлении (прогнозировании, аппроксимации) значения результирующего показателя по заданным значениям объясняющих переменных.
Наиболее удобные свойства (рекомендации по вычислению, по интерпретации, статистические свойства) выборочный коэффициент корреляции имеет в рамках линейно-нормальных моделей, т. е. в одном из двух типов ситуаций:
а) обрабатываемые статистические данные  образуют выборку из
образуют выборку из  -мерной нормальной генеральной совокупности;
-мерной нормальной генеральной совокупности;
б) результирующий показатель связан с объясняющими переменными линейной регрессионной зависимостью, причём остаточная случайная компонента подчиняется нормальному закону с постоянной (не зависящей от  ) дисперсией. В этом случае разработаны рекомендации по проверке выборочного множественного коэффициента корреляции на его статистически значимое отличие от нуля, по построению доверительных интервалов для неизвестного истинного значения множественного коэффициента корреляции.
) дисперсией. В этом случае разработаны рекомендации по проверке выборочного множественного коэффициента корреляции на его статистически значимое отличие от нуля, по построению доверительных интервалов для неизвестного истинного значения множественного коэффициента корреляции.
Анализ статистических связей между порядковыми переменными сводится к статистическому анализу различных упорядочений (ранжировок) одного и того же конечного множества объектов и осуществляется с помощью методов ранговой корреляции. Процесс упорядочения объектов производится либо с привлечением экспертов, либо формализованно — с помощью перехода от исходного ряда наблюдений косвенного количественного признака к соответствующему вариационному ряду в зависимости от типа изучаемой ситуации:
· шкала измерения анализируемого свойства не известна исследователю или отсутствует вовсе;
· существуют косвенные или частные количественные показатели, в соответствии со значениями которых можно определять место каждого объекта в общем ряду всех объектов, упорядоченных по анализируемому основному свойству.
Исходные статистические данные для проведения рангового корреляционного анализа представлены таблицей (матрицей) рангов статистически обследованных объектов размера  (число объектов на число анализируемых переменных). При формировании матрицы рангов допускаются случаи неразличимости двух или нескольких объектов по изучаемому свойству («объединённые» ранги).
(число объектов на число анализируемых переменных). При формировании матрицы рангов допускаются случаи неразличимости двух или нескольких объектов по изучаемому свойству («объединённые» ранги).
К основным задачам теории и практики ранговой корреляции относятся:
· анализ структуры исследуемой совокупности упорядочений (задача А);
· анализ интегральной (совокупной) согласованности рассматриваемых переменных и их условная ранжировка по критерию степени тесноты связи каждой из них со всеми остальными переменными (задача В);
· построение единого группового упорядочения объектов на основе имеющейся совокупности согласованных упорядочений (задача С).
Статистический анализ взаимосвязей порядковых переменных строится на базе различных вариантов моделей вероятностного пространства, в котором роль пространства элементарных исходов играет множество всех возможных перестановок из  элементов (
элементов ( — число статистически обследованных объектов).
— число статистически обследованных объектов).
В качестве основных характеристик парной статистической связи между упорядочениями используются ранговые коэффициенты корреляции Спирмэна  и Кендалла
и Кендалла  . Их значения меняются в диапазоне от - 1 до + 1, причём экстремальные значения характеризуют связь соответственно пары прямо противоположных и пары совпадающих упорядочений, а нулевое значение рангового коэффициента корреляции получается при полном отсутствии статистической связи между анализируемыми порядковыми переменными.
. Их значения меняются в диапазоне от - 1 до + 1, причём экстремальные значения характеризуют связь соответственно пары прямо противоположных и пары совпадающих упорядочений, а нулевое значение рангового коэффициента корреляции получается при полном отсутствии статистической связи между анализируемыми порядковыми переменными.
В качестве основной характеристики статистической связи между несколькими ( ) порядковыми переменными используется т. н. коэффициент конкордации (согласованности) Кендалла
) порядковыми переменными используется т. н. коэффициент конкордации (согласованности) Кендалла  . Между значениями этого коэффициента и значениями парных ранговых коэффициентов Спирмэна, построенных для каждой пары анализируемых переменных, существуют соотношения.
. Между значениями этого коэффициента и значениями парных ранговых коэффициентов Спирмэна, построенных для каждой пары анализируемых переменных, существуют соотношения.
Если представить себе, что каждому объекту некоторой достаточно большой гипотетической совокупности (генеральной совокупности) приписан какой-то ранг по каждой из рассматриваемых переменных и что статистическому обследованию подлежит лишь часть этих объектов (выборка объёма  ), то достоверность и практическая ценность выводов, основанных на анализе ранговой корреляции, существенно зависят от того, как ведут себя выборочные значения интересующих нас ранговых корреляционных характеристик при повторениях выборок заданного объёма, извлечённых из этой генеральной совокупности. Это и составляет предмет исследования статистических свойств выборочных ранговых характеристик связи. Результаты данного исследования относятся, прежде всего, к построению правил проверки статистической значимости анализируемой связи и к построению доверительных интервалов для неизвестных значений коэффициентов связи, характеризующих всю генеральную совокупность.
), то достоверность и практическая ценность выводов, основанных на анализе ранговой корреляции, существенно зависят от того, как ведут себя выборочные значения интересующих нас ранговых корреляционных характеристик при повторениях выборок заданного объёма, извлечённых из этой генеральной совокупности. Это и составляет предмет исследования статистических свойств выборочных ранговых характеристик связи. Результаты данного исследования относятся, прежде всего, к построению правил проверки статистической значимости анализируемой связи и к построению доверительных интервалов для неизвестных значений коэффициентов связи, характеризующих всю генеральную совокупность.
Парные и множественные характеристики ранговой корреляции являются удобным инструментом решения основных задач (А, В и С) статистического анализа связей между порядковыми переменными.
Корреляционное отношение это один из показателей тесноты связи. Общая формула корреляционного отношения:
 ,
,
где  - дисперсия условных средних
- дисперсия условных средних  , или
, или  , где
, где  — общая средняя;
— общая средняя;
 — дисперсия всех значений
— дисперсия всех значений  относительно их общей средней
относительно их общей средней  , или
, или  .
.
Числитель подкоренного выражения  может представлять и дисперсию значений, найденных по уравнению регрессии
может представлять и дисперсию значений, найденных по уравнению регрессии  , т. е.
, т. е.  .
.
В зависимости от того, какой из показателей берётся за числитель корреляционного отношения, говорят об эмпирическом и теоретическом корреляционном отношении. Теоретическое корреляционное отношение получается тогда, когда  является дисперсией значений, найденных по линии регрессии
является дисперсией значений, найденных по линии регрессии  относительно общей средней
относительно общей средней  . Эмпирическое корреляционное отношение будет в том случае, когда
. Эмпирическое корреляционное отношение будет в том случае, когда  явится дисперсией частных средних
явится дисперсией частных средних  .
.
Корреляционное отношение имеет следующие свойства. Оно всегда находится между 0 и 1. Оно равно 0, если между  и
и  не существует корреляционной связи. Оно равно 1, если зависимость между
не существует корреляционной связи. Оно равно 1, если зависимость между  и
и  является функциональной. С возрастанием значения корреляционного отношения от 0 до 1 связь между
является функциональной. С возрастанием значения корреляционного отношения от 0 до 1 связь между  и
и  становится теснее. Корреляционное отношение является мерой тесноты связи, как для линейной, так и для криволинейной формы связи, так как
становится теснее. Корреляционное отношение является мерой тесноты связи, как для линейной, так и для криволинейной формы связи, так как  может выражать и линейную и криволинейную корреляцию. Однако в случае линейной связи теоретическое корреляционное отношение совпадает с коэффициентом корреляции. Для криволинейных зависимостей корреляционное отношение является единственно правильным измерителем тесноты связи.
может выражать и линейную и криволинейную корреляцию. Однако в случае линейной связи теоретическое корреляционное отношение совпадает с коэффициентом корреляции. Для криволинейных зависимостей корреляционное отношение является единственно правильным измерителем тесноты связи.
Корреляционное отношение наряду с коэффициентом корреляции множественным является показателем степени связи между результативным и многими факториальными признаками; тогда  будет дисперсией условных средних
будет дисперсией условных средних  относительно общей средней
относительно общей средней  :
:
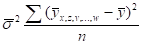
Следует заметить, что в силу правила сложения вариации  можно представить в виде разности между
можно представить в виде разности между  и дисперсией индивидуальных значений относительно условных средних (или соответственно относительно линии регрессии). Корреляционное отношение иногда называется индексом корреляции.
и дисперсией индивидуальных значений относительно условных средних (или соответственно относительно линии регрессии). Корреляционное отношение иногда называется индексом корреляции.
Коэффициент корреляции является показателем меры тесноты связи между зависимыми друг от друга статистическими величинами. Коэффициент корреляции представляет некоторое отвлечённое число, лежащее в пределах от - 1 до + 1. В случае линейной функциональной связи между зависимыми величинами коэффициент корреляции равен + 1 при прямой связи и — 1 при обратной связи. При отсутствии связи коэффициент корреляции равен 0. При положительной корреляции коэффициент корреляции находится в пределах от 0 до + 1, а при отрицательной корреляции — в пределах от 0 до -1. Коэффициент корреляции между  и
и  можно вычислить по формуле
можно вычислить по формуле
 ,
,
где  — соответствующие средние;
— соответствующие средние;  - средние квадратичные отклонения.
- средние квадратичные отклонения.
Удобно вычислять коэффициент корреляции по формуле
 .
.
Коэффициент корреляции можно представить и как среднюю геометрическую из коэффициентов регрессии, т.е. формулой  , где
, где  и
и  — коэффициенты регрессии
— коэффициенты регрессии  на
на  и
и  на
на  .
.
Вычисление коэффициента корреляции по всем приведённым формулам основывается на предположении о линейном характере зависимости. Однако коэффициент корреляции имеет значение и вне рамок линейной зависимости.
Множественный коэффициент корреляции является показателем тесноты связи при изучении влияния двух или более факторов на результат. Множественный коэффициент корреляции легко вычислить, зная линейные коэффициенты корреляции между каждой парой зависимых признаков. В случае линейной зависимости  от двух признаков (
от двух признаков ( и
и  ) множественный коэффициент корреляции исчисляется по формуле
) множественный коэффициент корреляции исчисляется по формуле
 ,
,
где  — соответствующие линейные коэффициенты корреляции между парами признаков.
— соответствующие линейные коэффициенты корреляции между парами признаков.  всегда положителен и заключается в пределах от 0 до 1. Между множественным коэффициентом корреляции
всегда положителен и заключается в пределах от 0 до 1. Между множественным коэффициентом корреляции  и двумя коэффициентами парной корреляции
и двумя коэффициентами парной корреляции  и
и  существует следующее соотношение: каждый из коэффициентов парной корреляции не может по абсолютной величине превышать
существует следующее соотношение: каждый из коэффициентов парной корреляции не может по абсолютной величине превышать  . Когда изучается зависимость между большим числом признаков, множественный коэффициент корреляции измеряющий зависимость от
. Когда изучается зависимость между большим числом признаков, множественный коэффициент корреляции измеряющий зависимость от  признаков (перенумерованных 1, 2, ...,
признаков (перенумерованных 1, 2, ...,  ) некоторого признака (занумерованного, например, нулём), можно рассчитать по формуле
) некоторого признака (занумерованного, например, нулём), можно рассчитать по формуле  , где
, где  — определитель:
— определитель:
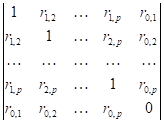
а знаменатель  — другой определитель, который можно получить из
— другой определитель, который можно получить из  , выбросив последнюю строку и последний столбец (здесь
, выбросив последнюю строку и последний столбец (здесь  — обыкновенный коэффициент корреляции между признаками ).
— обыкновенный коэффициент корреляции между признаками ).  и здесь представляет собой функцию парных коэффициентов корреляции.
и здесь представляет собой функцию парных коэффициентов корреляции.
Коэффициент корреляции рангов одна из мер тесноты связи. Коэффициент корреляции рангов Спирмена определяется по формуле
 ,
,
где  , т. е. разность между рангами взаимосвязанных признаков
, т. е. разность между рангами взаимосвязанных признаков  и
и  у отдельных единиц совокупности;
у отдельных единиц совокупности;  — число взаимосвязанных пар значений
— число взаимосвязанных пар значений  и
и  . Если связь между явлениями полная прямая, то ранги по
. Если связь между явлениями полная прямая, то ранги по  и
и  совпадут и
совпадут и  =0, тогда
=0, тогда  . Если связь полная обратная, то ранги по
. Если связь полная обратная, то ранги по  идут в обратном направлении рангам по
идут в обратном направлении рангам по  , тогда
, тогда  . Если связи нет,
. Если связи нет,  .
.
Другим способом измерения корреляции рангов служит исчисление коэффициент корреляции рангов Кендала по формуле
 ,
,
где  - сумма баллов, если баллом +1 оценивается пара рангов, имеющих по обоим признакам одинаковый порядок, а баллом -1 – пара рангов с обратным порядком;
- сумма баллов, если баллом +1 оценивается пара рангов, имеющих по обоим признакам одинаковый порядок, а баллом -1 – пара рангов с обратным порядком;  - то же, что и раньше.
- то же, что и раньше.
5. Автокорреляция
Автокорреляция это эффект отсутствия независимости между собой различных наблюдений. Наличие автокорреляции типично в тех случаях, когда исследуемая величина представляет собой временной ряд, т.е. её значения являются наблюдениями одной и той же величины в последовательные моменты времени. Например, при построении регрессионных моделей типа
 ………………. (5.1.)
………………. (5.1.)
где как объясняемая переменная  , так и независимые переменные (предикторы)
, так и независимые переменные (предикторы)  являются временными рядами, обычно нельзя считать ошибки
являются временными рядами, обычно нельзя считать ошибки  независимыми при разных
независимыми при разных  . Однако при наличии автокорреляции в ряду ошибок
. Однако при наличии автокорреляции в ряду ошибок  оценки параметров модели, полученные по методу наименьших квадратов, теряют эффективность.
оценки параметров модели, полученные по методу наименьших квадратов, теряют эффективность.
Статистика Дарвина — Уотсона предназначена для тестирования наличия автокорреляции остатков в регрессионных моделях вида (5.1.)
После оценивания параметров модели  по методу наименьших квадратов, возникает ряд остатков
по методу наименьших квадратов, возникает ряд остатков  . Статистику Дарвина — Уотсона обычно используют для статистической проверки наличия автокорреляции остатков. Статистика Дарвина — Уотсона выражается через значения остатков по формуле:
. Статистику Дарвина — Уотсона обычно используют для статистической проверки наличия автокорреляции остатков. Статистика Дарвина — Уотсона выражается через значения остатков по формуле:
 , (5.2.)
, (5.2.)
где  — ряд остатков, полученный после оценивания модельных коэффициентов. Выражение (5.2.) близко к величине
— ряд остатков, полученный после оценивания модельных коэффициентов. Выражение (5.2.) близко к величине  , где
, где  — выборочная автокорреляционная функция остатков. Соответственно, идеальное значение статистики — 2 (автокорреляция отсутствует). Меньшие значения соответствуют положительной автокорреляции остатков, большие — отрицательной. Статистика учитывает только автокорреляции первого порядка. Её применение теоретически обосновано лишь при использовании метода наименьших квадратов.
— выборочная автокорреляционная функция остатков. Соответственно, идеальное значение статистики — 2 (автокорреляция отсутствует). Меньшие значения соответствуют положительной автокорреляции остатков, большие — отрицательной. Статистика учитывает только автокорреляции первого порядка. Её применение теоретически обосновано лишь при использовании метода наименьших квадратов.
Распределение статистики Дарвина — Уотсона зависит от распределения независимых переменных  , входящих в уравнение регрессии. Однако можно указать две случайные величины
, входящих в уравнение регрессии. Однако можно указать две случайные величины  и
и  , зависящие лишь от ошибок
, зависящие лишь от ошибок  , между которыми заключено значение статистики
, между которыми заключено значение статистики  . Используя их распределения, можно оценить доверительную вероятность отклонения величины
. Используя их распределения, можно оценить доверительную вероятность отклонения величины  от 2 с двух сторон.
от 2 с двух сторон.
Один из возможных методов борьбы с явлением автокорреляции остатков — оценка коэффициентов модели с одновременной подгонкой авторегрессионной модели для ошибок  , например, по методу наибольшего правдоподобия (считая распределение ошибок гауссовским). Другой путь, приводящий к более простым вычислениям, основан на следующей идее. Пусть ошибки
, например, по методу наибольшего правдоподобия (считая распределение ошибок гауссовским). Другой путь, приводящий к более простым вычислениям, основан на следующей идее. Пусть ошибки  подчиняются авторегрессионной модели
подчиняются авторегрессионной модели  ,
,  — независимы,
— независимы,  — известно. Положим
— известно. Положим  ,
,  . Тогда
. Тогда  , и в этой новой модели ошибки
, и в этой новой модели ошибки  некоррелированы. Соответственно, предлагается оценить коэффициенты модели по методу наименьших квадратов в исходной модели, затем к ряду остатков подогнать авторегрессионную модель невысокого порядка, и заново оценить регрессионные коэффициенты по преобразованным данным. Статистические свойства метода плохо исследованы.
некоррелированы. Соответственно, предлагается оценить коэффициенты модели по методу наименьших квадратов в исходной модели, затем к ряду остатков подогнать авторегрессионную модель невысокого порядка, и заново оценить регрессионные коэффициенты по преобразованным данным. Статистические свойства метода плохо исследованы.
Для стационарных временных рядов (или, в другой терминологии, стационарных процессов и последовательностей)  понятие автокорреляции имеет особое значение, поскольку их исследование во многом сводится к исследованию их автокорреляционной структуры. Одной из важнейших характеристик стационарной последовательности (ряда) является её автокорреляционная функция
понятие автокорреляции имеет особое значение, поскольку их исследование во многом сводится к исследованию их автокорреляционной структуры. Одной из важнейших характеристик стационарной последовательности (ряда) является её автокорреляционная функция  ,
,  , где
, где  есть коэффициент корреляции между
есть коэффициент корреляции между  и
и  (иногда так называют автокорреляционную функцию
(иногда так называют автокорреляционную функцию  , где
, где  — среднее значение). Иногда удобно считать
— среднее значение). Иногда удобно считать  определённым при
определённым при  , считая
, считая  ,
,  .
.
Автокорреляционная функция всегда обладает свойством положительной определённости: для любых чисел  и любых целых чисел
и любых целых чисел  величина
величина
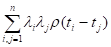
неотрицательна. Для эргодических процессов  при
при  .
.
С автокорреляционной функцией тесно связана частная автокорреляционная функция  , определяемая как частный коэффициент корреляции между
, определяемая как частный коэффициент корреляции между  и
и  при исключённом влиянии
при исключённом влиянии  . Частная автокорреляционная функция играет роль при подгонке авторегрессии моделей, поскольку если временной ряд адекватно описывается моделью авторегресии порядка
. Частная автокорреляционная функция играет роль при подгонке авторегрессии моделей, поскольку если временной ряд адекватно описывается моделью авторегресии порядка  , то его частная автокорреляционная функция
, то его частная автокорреляционная функция  равна нулю при
равна нулю при  .
.
Другой характеристикой автокорреляционной структуры стационарного ряда является его спектральная мера  , связанная с его автоковариационной функцией
, связанная с его автоковариационной функцией по формуле
по формуле
 ,
,
и спектральная плотность  .
.
Аналогичное представление имеет место и для процессов с непрерывным временем, но в этом случае  меняется в пределах от 0 до
меняется в пределах от 0 до  . Спектральная плотность всегда неотрицательна и характеризует вклад различных частотных компонент в общую дисперсию процесса. Для последовательности независимых одинаково распределённых случайных величин спектральная плотность является константой.
. Спектральная плотность всегда неотрицательна и характеризует вклад различных частотных компонент в общую дисперсию процесса. Для последовательности независимых одинаково распределённых случайных величин спектральная плотность является константой.
6. Модель авторегресии
Модель авторегресии - модель, в которой текущее значение процесса объясняется через его предшествующие значения. В стандартной форме линейная модель записывается в виде
 , (6.1.)
, (6.1.)
где  - объясняемая переменная, a
- объясняемая переменная, a  — ошибки («белый шум»). Величина
— ошибки («белый шум»). Величина  называется порядком модели. Часто в модель включают также константу, применяя модель (6.1) не к исходному процессу
называется порядком модели. Часто в модель включают также константу, применяя модель (6.1) не к исходному процессу  , а к центрированному
, а к центрированному  .
.
Модель авторегресии используется для описания стационарных временных рядов. Процесс, определяемый моделью (6.1), стационарен, если все корни полинома
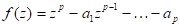
лежат внутри единичного круга  .
.
Через авторегрессионные коэффициенты  можно вычислить все статистические характеристики процесса
можно вычислить все статистические характеристики процесса  . В частности, автокорреляционная функция
. В частности, автокорреляционная функция  ряда
ряда  удовлетворяет системе уравнений
удовлетворяет системе уравнений
 .
.
Подставляя в качестве  значения 1, 2, ...,
значения 1, 2, ...,  , получаем систему уравнений, связывающих первые
, получаем систему уравнений, связывающих первые  значений автокорреляционной функции
значений автокорреляционной функции  с коэффициентами
с коэффициентами  :
:
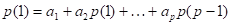
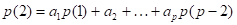
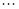
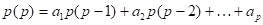
Эти уравнения обычно называют уравнениями Юла — Уокера. Они могут быть использованы для оценивания коэффициентов авторегрессии, если в них заменить теоретические значения автокорреляций соответствующими выборочными значениями.
Поведение процесса, описываемого моделью авторегресии первого порядка, зависит от знака авторегрессионного коэффициента  . Положительный коэффициент соответствует присутствию долгопериодических колебаний, отрицательный — сильной осцилляции. Поведение процесса авторегрессии второго порядка зависит от расположения корней полинома
. Положительный коэффициент соответствует присутствию долгопериодических колебаний, отрицательный — сильной осцилляции. Поведение процесса авторегрессии второго порядка зависит от расположения корней полинома  . Если его корни являются мнимыми, процесс содержит квазипериодические колебания с некоторой фиксированной частотой. Примером подобного ряда могут служить числа Вольфа (солнечная активность).
. Если его корни являются мнимыми, процесс содержит квазипериодические колебания с некоторой фиксированной частотой. Примером подобного ряда могут служить числа Вольфа (солнечная активность).
Выбор порядка авторегрессии на практике помогает осуществить исследование автокорреляционной структуры процесса. А именно, для процесса авторегрессии порядка  значения его частной автокорреляционной функции
значения его частной автокорреляционной функции  равны нулю при
равны нулю при  . Для оценок коэффициентов модели авторегресии может быть использован как метод наименьших квадратов (вообще говоря, не эффективен), так и метод максимума правдоподобия. Обобщением модели авторегресии являются смешанная модель авторегрессии и скользящего среднего (АРСС) и модель Бокса — Дженкинса, или АРИСС, описывающая в т.ч. нестационарные процессы. Модель АРСС возникает из модели авторегрессии в случае, когда ошибки
. Для оценок коэффициентов модели авторегресии может быть использован как метод наименьших квадратов (вообще говоря, не эффективен), так и метод максимума правдоподобия. Обобщением модели авторегресии являются смешанная модель авторегрессии и скользящего среднего (АРСС) и модель Бокса — Дженкинса, или АРИСС, описывающая в т.ч. нестационарные процессы. Модель АРСС возникает из модели авторегрессии в случае, когда ошибки  являются не белым шумом, а процессом скользящего среднего некоторого порядка
являются не белым шумом, а процессом скользящего среднего некоторого порядка  :
:
 ,
,
где  — «белый шум».
— «белый шум».
В свою очередь, процесс  описывается моделью АРИСС, если его приращения
описывается моделью АРИСС, если его приращения  порядка
порядка  описываются моделью АРИСС (
описываются моделью АРИСС ( ). Модели Бокса — Дженкинса являются весьма гибкими моделями, позволяющими строить хорошие аппроксимации для многих временных рядов.
). Модели Бокса — Дженкинса являются весьма гибкими моделями, позволяющими строить хорошие аппроксимации для многих временных рядов.
Литература
Бесплатная лекция: "2.3. Основные задачи информационных систем (ИС)" также доступна.
1. Бокс Д ж ., Дженкиис Т., Анализ временных рядов. Прогноз и управление, вып. 1, М., 1974
2. Маленво Э., Статистические методы эконометрии, вып. 2, М., 1976.
3. Кенделл М., Временные ряды, М, 1981.
4. Андерсон Т., Статистический анализ временных рядов, М., 1976
5. Себер Дж ., Линейный регрессионный анализ, М., 1980
6. Песаран Л.,Слейтер Т., Динамическая регрессия: теория и алгоритмы, М., 1984.






















