Стохастическая аппроксимация

6. Стохастическая аппроксимация

Под стохастической аппроксимацией понимается общее название ряда конкретных методов решения задач статистического оцени­вания. Эти методы объединяет то, что все они носят рекуррент­ный характер, т. е. имеющаяся к текущему моменту времени оценка уточняется тем или иным способом при поступлении но­вого наблюдения. Термин стохастическая аппроксимация был введён американскими мате­матиками X. Роббинсом и С. Монро, предложившими в 1951 процедуру рекуррентного нахождения корня уравнения регрес­сии. В 1952 Дж. Кифер и Дж. Вольфовиц предложили процеду­ру итеративного нахождения экстремума функции регрессии.

Функцией регрессии называется математическое ожидание слу­чайной величины, зависящей от параметра как функция этого параметра. Параметр может быть как скалярным, так и вектор­ным. Пусть  - случайная величина, зависящая от скалярно­го параметра ,

.

Требуется определить значение , при котором

.                                     (5.1)

Здесь М означает математическое ожидание, d - заданное чис­ло. Таким образом,  - корень уравнения регрессии (5.1). Если плотность распределения  как функция х нам известна, то задача (5.1) становится обычной задачей численного анализа. Од­нако, как правило, плотность распределения нам не известна, а доступны лишь наблюдения  реализаций случайной величи­ны  при фиксированном х. Эти наблюдения можно использо­вать для рекуррентной оценки (аппроксимации) х с помощью процедуры стохастической аппроксимации (Роббинс, Монро, 1951):

                             (5.2.)

Здесь  — последовательность оценок величины , полученных на предыдущих шагах,

Рекомендуемые материалы

,

- случайная величина такая, что

.                        (5.3)

Символ означает условное математическое ожи­дание при фиксированных х₁,х₂.....

Обычно в качестве  выбирается реализация  случайной величины Y(x_n) на шаге п алгоритма (5.2). Равенство (5.3) будет обеспечено, например, если  независимы при разных п. При некоторых условиях на  и дисперсию  процесс (5.2) сходится почти всюду и в среднем квадратическом к . Процесс (5.2) напоминает детерминированный итерационный процесс нахож­дения корня одномерного уравнения и действительно превращает­ся в таковой в случае, когда  обычная (не случайная) функ­ция параметра . Процедура стохастической аппроксимации для отыскания такого значения х_э, при котором  достигает экстремума (максимума), имеет вид (Кифер, Вольфовиц, 1952)

,

, , ,                      (5.4.)

Бесплатная лекция: "2.1. Основные этапы процесса маркетинговых исследований" также доступна.

, ,

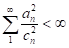
Смысл обозначений  тот же самый, что и в процессе (5.2). При определённых предположениях на MY и DY процесс (5.4) сходится к х_э почти всюду и в среднем квадратичном. Процесс (5.4) является стохастическим аналогом градиентного метода нахождения точки экстремума функции, при этом вместо градиента вычисляется аппроксимирующее его разностное отно­шение. Существуют многомерные (х и  - векторы) обоб­щения процедур (5.2) и (5.4). Исследовалась проблема оптимально­го (в некотором смысле) выбора параметров а_п и с_п.

Некоторое представление о возможных применениях процес­сов стохастической аппроксимации может дать следующий пример. Пусть некоторое про­изводство характеризуется величиной выпуска , зависящей от •«технологии» х и случайного параметра .

 могут быть как скалярными, так и векторными величина­ми. Предположим, что случайный параметр характеризует чисто­ту исходного продукта. Чтобы обеспечить заданную или экстре­мальную величину выпуска , необходимо выбрать технологию  в соответствии с конкретным реализованным значением . Су­щественная смена технологии каждый раз при поступлении новой партии сырья (новой реализации ) часто бывает невозможна. В такой ситуации более целесообразно пытаться управлять величи­ной математического ожидания выпуска MY(x), выбирая управ­ляющий параметр х так, чтобы обеспечить её максимальный или заданный уровень. Такой подбор может быть осуществлён в пе­риод опытной эксплуатации путём итерационного изменения пара­метра  по формулам типа (5.2) или (5.4). Уточнение технологии в такой ситуации возможно и в процессе нормальной эксплуатации.

Стохастическая аппроксимация позволяет уточнять параметры модели, обеспечивающие в среднем требуемый или экстремальный результат в процессе накопления наших знаний о действии случайных факторов.

Процедуры стохастической аппроксимации обобщены в различных направлениях. В ча­стности, предложены и изучены методы стохастической аппроксимации в ситуации, когда наложены априорные ограничения на множество возможного изменения параметра . Эти методы используются для получе­ния приближённых решений задач стохастического программи­рования. Методы стохастической аппроксимации широко используются в теории автома­тического управления, статистической теории распознавания об­разов и смежных областях.