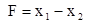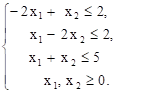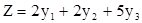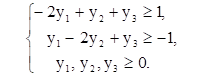Модели линейной оптимизации
Модели линейной оптимизации.
Двойственность и основные соотношения двойственности
К моделям линейной оптимизации относятся задачи на максимум или минимум линейной целевой функции многих переменных при ограничениях на них в форме линейных равенств и неравенств.
С любой экономико-математической задачей, для которой можно построить линейную модель, либо свести к построению линейной модели, связана двойственная задача. Прямая и двойственная задача тесно взаимосвязаны, так как оптимальное решение одной задачи можно получить непосредственно, зная оптимальное решение другой задачи. Совместное изучение прямой задачи и двойственной к ней дает, как правило, значительно больше информации.
Рассмотрим решения прямой и двойственной задач графическим методом, с помощью которого легко иллюстрируются основные соотношения теории двойственности.
Пример 1. Решить графическим методом прямую и двойственную задачи (табл. 1).
Таблица 1
Решение прямой задачи.
Строим область допустимых решений задачи. Для этого нумеруем ограничения задачи

В прямоугольной декартовой системе координат (рис. 2) строим прямую  (p1), соответствующую ограничению (1) по двум точкам, например, (– 7; 0) и (– 4; 2). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая p1 не проходит через начало координат, подставляем координаты точки
(p1), соответствующую ограничению (1) по двум точкам, например, (– 7; 0) и (– 4; 2). Находим, какая из полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство. Так как прямая p1 не проходит через начало координат, подставляем координаты точки  в первое ограничение
в первое ограничение  . Получаем строгое неравенство
. Получаем строгое неравенство  . Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую
. Следовательно, точка О лежит в полуплоскости решений. Штриховкой отмечаем полуплоскость, содержащую точку О. Аналогично строим прямую  (p2) по двум точкам (0; 8) и (8; 0) и определяем область решений ограничения (2).
(p2) по двум точкам (0; 8) и (8; 0) и определяем область решений ограничения (2).
 |



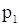

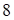

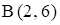
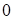
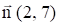
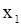

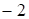
 |
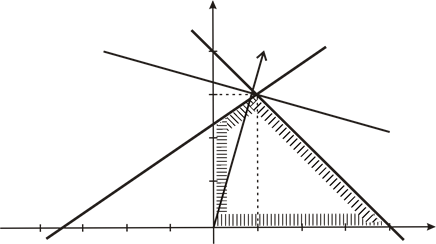
Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Полученная область допустимых решений на рисунке заштрихована и представляет собой ограниченный выпуклый многоугольник ОАВС.
Строим нормаль линий уровня  . Так как решается задача на отыскание максимума целевой функции, то линию уровня
. Так как решается задача на отыскание максимума целевой функции, то линию уровня  перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.
перемещаем в направлении нормали до угловой точки В, которая расположена на прямой, называемой опорной. Эта опорная прямая проходит через точку В пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (1) и (2), перпендикулярно нормали.
Определяем координаты точки В как пересечение прямых p1 и p2. Для этого решаем систему

Получаем:

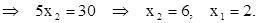
Следовательно, координаты точки  . Оптимальное решение х1* = 2, х2* = 6. Вычисляем максимум целевой функции:
. Оптимальное решение х1* = 2, х2* = 6. Вычисляем максимум целевой функции:  Уравнение опорной прямой имеет вид:
Уравнение опорной прямой имеет вид: 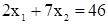
Решение двойственной задачи.
Для построения области допустимых решений занумеруем ограничения задачи:
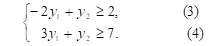
Строим прямые p3 и p4, уравнения которых: – 2у1 + у2 = 2 и 3у1 + у2 = 7. Учитывая условия неотрицательности переменных, определяем область допустимых решений. Полученная область представляет неограниченный сверху выпуклый многоугольник (рис. 3). Нормаль линии уровня  .
.
В данной задаче необходимо найти минимум целевой функции, поэтому линию уровня перемещаем в направлении, противоположном направлению нормали до опорной прямой. Эта прямая проходит через точку D пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (3) и (4), перпендикулярно нормали.
Определяем координаты точки D, как пересечение прямых p3 и p4. Для этого решаем систему
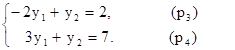
Получаем, что точка D имеет координаты  . Оптимальное решение у1* = 1, у2* = 4. Вычисляем минимум целевой функции:
. Оптимальное решение у1* = 1, у2* = 4. Вычисляем минимум целевой функции:  Уравнение опорной прямой имеет вид:
Уравнение опорной прямой имеет вид:  .
.
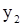 | |||||
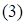 | |||||
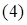 | |||||
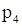
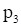
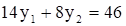
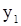
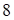
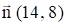
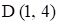



 |
Как видно из приведенных решений прямой и двойственной задач значения целевых функций равны: 
При любом допустимом решении прямой задачи значение целевой функции « » (не превосходят) значений целевой функции двойственной задачи при ее допустимом произвольном решении.
» (не превосходят) значений целевой функции двойственной задачи при ее допустимом произвольном решении.
Например, при допустимом решении прямой задачи  значение целевой функции
значение целевой функции  , а при допустимом двойственной задачи
, а при допустимом двойственной задачи  значение целевой функции
значение целевой функции  , т.е.
, т.е.  .
.
Пример 2. Решить графическим методом прямую и двойственную задачи (табл. 2).
Таблица 2
| Прямая задача | Двойственная задача |
| Минимизировать при ограничениях
| Максимизировать при ограничениях
|
Для решения прямой задачи вводим нумерацию ограничений задачи:
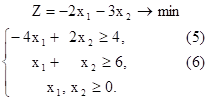
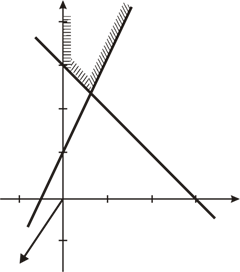
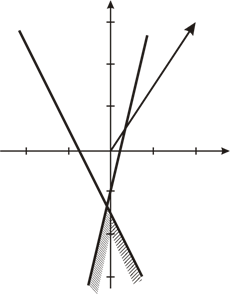
Аналогично примеру 1 строим область допустимых решений, которая представляет собой выпуклый многоугольник не ограниченный сверху. Нормаль линии уровня  (рис. 4).
(рис. 4).
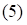 | |||
 | |||
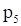
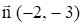
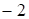
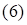
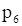
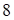
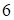
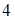
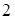
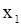
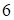
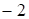
 |
В данной задаче необходимо найти минимум целевой функции, поэтому линию уровня перемещаем в направлении, противоположном направлению нормали, которая уходит в бесконечность. Задача не имеет оптимального решения из-за неограниченности снизу целевой функции  на множестве допустимых решений.
на множестве допустимых решений.
Решение двойственной задачи.
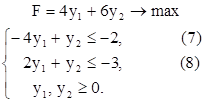
Область допустимых решений для данной задачи представляет собой пустое множество, что означает противоречивость системы ограничений (рис. 5). Следовательно, и двойственная задача, так же как и прямая задача, не имеет решения.
 |
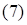
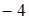
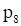
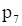
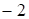
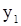
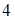
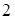
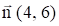
 |
Взаимозависимость оптимальных решений пары двойственных задач определена следующими соотношениями:
Теорема (основное неравенство). Пусть Х – какое-нибудь допустимое решение прямой задачи, а Y – какое-нибудь допустимое решение двойственной задачи. Тогда справедливо неравенство
 .
.
Следствие 1 (достаточный признак оптимальности). Если для каких-то допустимых решений  и
и  соответственно прямой и двойственной задач выполняется равенство
соответственно прямой и двойственной задач выполняется равенство
 ,
,
то  есть оптимальное решение прямой задачи, а
есть оптимальное решение прямой задачи, а  – оптимальное решение двойственной задачи.
– оптимальное решение двойственной задачи.
Следствие 2. Если в одной из пары двойственных задач целевая функция не ограничена с соответствующей стороны (т.е.  в прямой задаче или
в прямой задаче или  в двойственной задаче), то другая задача не имеет допустимых решений.
в двойственной задаче), то другая задача не имеет допустимых решений.
Основная теорема. Если разрешима одна из пары двойственных задач, то разрешима и другая задача, причем  .
.
Остальные теоремы двойственности будут сформулированы в следующих разделах данного пособия.
Для понимания экономической интерпретации основных соотношений двойственности рассмотрим модель распределения ограниченных ресурсов, в которой целевая функция, отображающая прибыль или доход от производственной деятельности, подлежит максимизации.
Формулировка прямой задачи
Пусть фирма располагает m видами ресурсов Р1 , Р2 ,… Рm и планирует организовать выпуск из них n видов продукции П1 , П2 ,…, Пn .
Известны следующие исходные данные:
aij – нормы расхода i-го ресурса на изготовление одной единицы j-ой продукции Пj;
cj - прибыль от реализации одной единицы j-ой продукции Пj;
bi - количество ресурса i–го вида.
Требуется составить план выпуска продукции П1, П2,…Пn. из имеющихся объемов ресурсов Р1, Р2 ,…Рm , при котором прибыль от ее реализации будет максимальной.
Построим математическую модель этой задачи.
Обозначим за xj (j = 1,2,...,n) – число единиц продукции, запланированных к производству. Тогда прибыль от реализации j-го вида продукции составит cj∙xj , а суммарная прибыль от реализации всей продукции будет равна:
F = c1 x1 + c2 x2 + ...+ cn xn.
Согласно условиям задачи, она подлежит максимизации.
Затраты ресурса Pi на выпуск всей продукции Х = (x1, x2 ,..., xn ) будут выражаться суммой произведений норм расхода aij на объемы выпуска и составят величину, равную ai1 x1 + ai2 x2 + ... + ain xn . Поскольку запас ресурса Рi равен bi , а расход ресурса не может превышать имеющегося его количества, то приходим к ограничениям следующего вида:
ai1x1 + ai2x2 +… + ainxn £ bi, i = 1,2,...,m
Учитывая естественные условия неотрицательности объемов выпуска продукции,
xj 0, j=1,2,...,n,
0, j=1,2,...,n,
придем к следующей задаче:
Найти такой план Х = (x1, x2 ,..., xn) выпуска продукции, удовлетворяющий системе неравенств
 a11x1 + a12x2 + … + a1nxn £ b1,
a11x1 + a12x2 + … + a1nxn £ b1,
a21x1 + a22x2 + … + a2nxn £ b2,
… … … … … … …
ai1x1 + ai2x2 + … + ainxn £ bi,
… … … … … … …
am1x1 + am2x2 + … + amnxn £ bm,
xj ³ 0, j = 1, 2, …, n,
при котором функция F = c1x1 + c2x2 + … + cnxn принимает максимальное значение.
Формулировка двойственной задачи
Предположим, что некоторая организация решила закупить ресурсы Р1 , Р2 ,…, Рm фирмы и необходимо определить цены на эти ресурсы у1, у2,…, уm. Естественно, что покупающая организация заинтересована в том, чтобы затраты на покупку ресурсов в объеме b1, b2,…, bm по ценам у1, у2,…, уm были минимальны, то есть Z = b1y1 + b2y2 + … +bmym ® min.
Предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции j-го вида расходуется сырье Р1 в объеме а1j, сырье Р2 в объеме а2j…, сырье Рm в объеме аmj по цене у1, у2,…, уm соответственно, то есть затраты на изготовление продукции Пj должны быть не меньше, чем цена ее реализации. Приходим к ограничениям следующего вида:
а1jу1 + а2jу2 + … + аmjуm ≥ сj , j=1,2,...,n.
Учитывая условия неотрицательности цены единицы i-го ресурса, приходим к следующей задаче:
Найти такой вектор У = (у1, у2 ,..., уm) – цен ресурсов, удовлетворяющий системе неравенств
 a11у1 + a21у2 + … + am1уm ≥ c1,
a11у1 + a21у2 + … + am1уm ≥ c1,
a12y1 + a22y2 + … + am2ym ≥ c2,
… … … … … … …
a1jy1 + a2jy2 + … + amjym ≥ cj,
… … … … … … …
a1ny1 + a2ny2 + … + amnym ≥ cn,
yi ³ 0, i = 1, 2, …, m,
при котором функция Z = b1y1 + b2y2 + …+ bmym принимает минимальное значение.
Цены ресурсов в экономической литературе имеют различные названия: учетные, неявные, теневые, объективно-обусловленные оценки (о-о оценки). Смысл этих названий состоит в том, что это условные (ненастоящие) цены. Эти цены определяются в ходе решения задачи, их называют оценками ресурсов.
Сопоставим общие представления прямой и двойственной задач в табл. 3, причем прямая задача – это задача модели распределения ограниченных ресурсов.
Таблица 3
| Прямая задача | Двойственная задача |
| Максимизировать F = при ограничениях
xj ³ 0, j = 1, 2, …, n, | Минимизировать Z = при ограничениях
yi ³ 0, i=1,2,...,m |
Сравнивая рассмотренные примеры видно, что двойственная задача по отношению к исходной составляется согласно следующим правилам.
1. Если первая задача имеет размеры  (m–ограничений с n неизвестными), то вторая – размеры
(m–ограничений с n неизвестными), то вторая – размеры  .
.
2. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными.
З. В правых частях ограничений в каждой задаче стоят коэффициенты при неизвестных в целевой функции другой задачи.
4. В прямой задаче все ограничения представляют собой неравенства типа « », причем в этой задаче требуется достичь
», причем в этой задаче требуется достичь  . Напротив, в двойственной задаче все ограничения суть неравенства типа «
. Напротив, в двойственной задаче все ограничения суть неравенства типа « », причем требуется достичь
», причем требуется достичь  .
.
Графически эти правила представлены в таблице 4.
Таблица 4
| Переменные двойственной задачи | Переменные прямой задачи | ||||||
| х1 | х2 | … | хi | … | xn | ||
| c1 | c2 | … | ci | … | cn | ||
| y1 y2 . . . yn | a11 a21 . . . am1 | a12 a22 . . . am2 | … … … … | a1i a2i . . . ami | … … … … | a1n a2n . . . amn | b1 b2 . . . bm |
| j-е ограничение двойственной задачи | коэффициенты целевой функции двойственной задачи |
Экономическое содержание основной теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенства общей оценки продукции и ресурсов и показывают убыточность всякого другого плана, отличного от оптимального.
Из приведенных соотношений видно, что для всех допустимых решений прямой и двойственной задач значения целевой функции задачи минимизации всегда будет верхним пределом значения целевой функции задачи максимизации. Таким образом, итерационное решение задачи максимизации ведет к возрастанию значения целевой функции, а итерационное решение задач минимизации – к ее убыванию. В итоге, при успешном завершении процессов вычисления прямой и двойственной задач приходят к точке «равновесия», где значения целевых функций задач максимизации и минимизации становятся равными.
Имеет место следующая теорема равновесия, используя которую можно находить решение одной из двойственных задач, зная решение другой задачи.
Теорема равновесия. Пусть Х* – какое-нибудь допустимое решение прямой задачи, а Y* – какое-нибудь допустимое решение двойственной задачи. Для одновременной оптимальности этих решений необходимо и достаточно выполнение равенств:
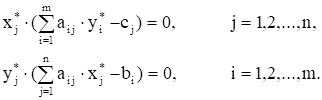
Величины, стоящие в скобках сформулированной теоремы, равны разности между левой и правой частями ограничения одной из двойственных задач на соответствующую переменную другой задачи.
Учитывая условия неотрицательности переменных и знаки сомножителей в произведениях, можно получить следующее:
если какое-либо ограничение одной задачи на оптимальном плане выполняется как строгое неравенство, то соответствующая координата оптимального плана другой задачи равна нулю:
Если ai1 x1* + ai2 x2*+ ... + ain xn* < bi , то yi* = 0 .
Если a1j y1* + a2j y2*+ … + amj ym* > cj , то xj* = 0 .
Если какая-либо координата оптимального плана одной задачи положительна, то соответствующее ограничение другой задачи обращается в равенство:
Если yi* > 0 , то ai1 x1* + ai2 x2*+ ... + ain xn* = bi .
Если xj* > 0 , то a1j y1* + a2j y2*+ … + amj ym* = cj .
Экономическое содержание теоремы равновесия означает, что если по некоторому оптимальному плану Х* производства расход i-го ресурса строго меньше его запаса bi, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равно нулю. Если же в некотором оптимальном плане оценок его i-ая координата строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует, что двойственные оценки служат мерой дефицитности ресурсов. Дефицитный ресурс, который полностью используется по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, не используемый полностью, имеет нулевую оценку.
Пример 3. Используя теорему равновесия, решить пару двойственных задач (табл.5).
Таблица 5
| Прямая задача | Двойственная задача |
| Максимизировать при ограничениях
| Минимизировать
при ограничениях
|
Решим прямую задачу графическим методом.
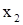 |
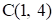
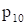

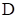
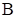
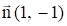
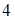
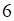
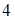
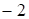
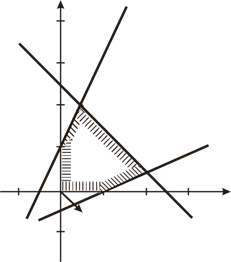
Рис. 6
Аналогично примеру 1 строим область допустимых решений, которая представляет собой выпуклый многоугольник ОАВСD. Нормаль линии уровня  (рис. 6).
(рис. 6).
Определяем координаты точки С как пересечение прямых p9 и p10. Для этого решаем систему
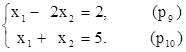
Получаем:

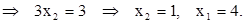
Следовательно, координаты точки  . Оптимальное решение х1* = 4, х2* = 1. Вычисляем максимум целевой функции прямой задачи:
. Оптимальное решение х1* = 4, х2* = 1. Вычисляем максимум целевой функции прямой задачи: 
По основной теореме двойственности Z(Y*) = F(Х*) = 3. Подставим Х* = (4;1) в систему ограничений прямой задачи:

Первое ограничение прямой задачи на оптимальном плане выполняется как строгое неравенство, следовательно, соответствующая переменная двойственной задачи равна нулю: y1*= 0.
Второе и третье ограничение прямой задачи обращается в точное равенство, следовательно, соответствующие переменные двойственной задачи положительны: y2* > 0 и y3* > 0.
Условия равновесия можно записать в виде равенств:
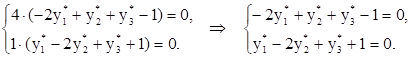
Ещё посмотрите лекцию "2 Блок питания ПЭВМ" по этой теме.
Подставляя y1*=0 в последнюю систему уравнений, получим систему:
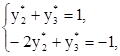
откуда получаем, что y2* =  , y3* =
, y3* =  .
.
Оптимальное решение двойственной задачи Y*= (0;  ;
; ) при этом минимум целевой функции двойственной задачи: Zmin = Z(Y*) = 3.
) при этом минимум целевой функции двойственной задачи: Zmin = Z(Y*) = 3.
Графический способ решения задач показывает, что оптимальное решение задач, сводящихся к линейным моделям, всегда ассоциируется с угловой точкой области допустимых решений.
Переход от геометрического способа решения задач к симплекс-методу лежит через алгебраическое описание угловых точек области допустимых решений. Для реализации этого перехода сначала надо привести задачу к канонической форме, преобразовав неравенства ограничений в равенства путем введения дополнительных переменных. Каноническая форма задачи необходима, потому что она позволяет получить базисное решение, которое полностью определяет все (геометрические) крайние точки пространства решений. Симплекс-метод позволяет эффективно найти оптимальное решение среди всех базисных.



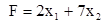



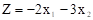


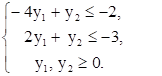
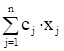
 ; i=1,2,...,m
; i=1,2,...,m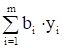
 ; j = 1, 2, …, n
; j = 1, 2, …, n