Принятие решений в условиях риска
§ 13. Принятие решений в условиях риска
Как и в случае принятия решения в условиях неопределенности здесь решение принимается в условиях ограниченности или неточности информации. Степень неполноты данных выражается через функцию распределения.
С точки зрения наличия исходных данных определенность и неопределенность представляет два крайних случая, а риск определяет промежуточную ситуацию.
Мы будем рассматривать следующие критерии принятия решения в условиях риска:
1) критерий ожидаемого значения (прибыль или расход);
2) комбинация ожидаемого значения и дисперсии;
3) критерий известного предельного уровня;
4) критерий наиболее вероятного события в будущем.
1. Критерий ожидаемого значения
Количественно этот критерий можно выразить в денежных единицах или в единицах полезности денег. Продемонстрируем это на примере. Предположим, что инвестиции $20 тыс. дают с равными вероятностями либо нулевой доход, либо $100 тыс. В денежных единицах ожидаемый доход составляет:
Рекомендуемые материалы
0,5·0 + 0,5·100 – 20 = $30 тыс.
Можно принять решение о вложении денег, однако это решение не в равной степени приемлемо для всех вкладчиков. Допустим имеются два вкладчика А и В. У А средства ограничены и потеря $20 тыс. приведет его к банкротству. В имеет средства значительно превышающие $20 тыс., это бездействующий капитал и он может рисковать.
Предположим, что Z – случайная величина с математическим ожиданием EZ и дисперсией DZ. Пусть имеется выборка z1, z2,…, zn объема n. Тогда выборочное среднее равно  .
.
Выборочное среднее имеет дисперсию
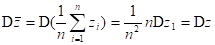
При n → ∞  .
.
Отсюда, можно сделать следующий вывод: использование критерия ожидаемого значения допустимо лишь в том случае, когда одно и то же решение приходится принимать достаточно большое число раз.
Пример 1. Предположим, что есть необходимость профилактического ремонта оборудования. Требуется принять решение о том, когда следует проводить ремонт какого-либо станка чтобы минимизировать потери. Если весь временной отрезок разбит на равные периоды, то решение заключается в определении оптимального числа периодов между двумя периодами.
Предположим, что имеется n станков, через Т интервал времени выполняется профилактический ремонт всех n станков.
Определить оптимальное значение Т, при котором минимизируются затраты на ремонт вышедших из строя станков и проведение профилактического ремонта в расчете на один интервал времени.
Пусть Рt – вероятность выхода из строя одного станка в момент времени Т ; nt – случайная величина, число вышедших из строя станков (имеет биномиальное распределение с параметрами n, pt, таким образом математическое ожидание Ent = npt); c1 – затраты на ремонт вышедшего из строя станка; c2 – затраты на профилактический ремонт; EC(T) – ожидаемые затраты за один интервал времени. Из условий получим
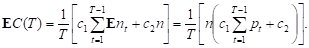
Требуется найти значение Т, удовлетворяющее условиям
 .
.
Покажем это на нашем примере.
Пусть С1 = 100, С2 = 10, n = 50. Составим следующую таблицу:
|
| Pt | EC(T) | |
| 1 | 0,05 | 0 | 500 |
| 2 | 0,07 | 0,05 | 375 |
| 3 | 0,10 | 0,12 | 366,7 |
| 4 | 0,13 | 0,22 | 400 |
| 5 | 0,18 | 0,35 | 450 |
Из таблицы видно, что Т* = minT = 366,7. Т.е. ремонт следует производить через 3 периода.
2. Критерий ожидаемое значение – дисперсия
 Предположим, что z – случайная величина с дисперсией Dz.
Предположим, что z – случайная величина с дисперсией Dz.
 Выборочное среднее имеет дисперсию
Выборочное среднее имеет дисперсию
Если дисперсия Dz уменьшается, то дисперсия  также уменьшается, и это означает, что вероятность того, что
также уменьшается, и это означает, что вероятность того, что  будет приближаться к Ez, увеличивается.
будет приближаться к Ez, увеличивается.
В условиях этого критерия выбирается:
max{Ez – kDz} или min{Ez + kDz},
где k – уровень не склонности к риску (постоянная величина).
Пример 2. В условиях предыдущего примера посчитаем дисперсию затрат за один период времени.
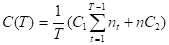 |
где nt – случайная величина, которая имеет биномиальное распределение (nt ~ Dnt = nPt(1-Pt)).
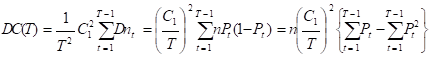 |
Выбираем то значение Т, которое удовлетворяет:
min{EC(T) + kDC(T)}.
Пусть k = 1, С1 = 100, С2 = 10, n = 50.
|
| Pt | Pt2 |
|
| EC(T)+DC(T) |
| 1 | 0,05 | 0,0025 | 0 | 0 | 500 |
| 2 | 0,07 | 0,0049 | 0,05 | 0,025 | 6312,5 |
| 3 | 0,10 | 0,01 | 0,12 | 0,074 | 6622,22 |
| 4 | 0,13 | 0,0169 | 0,22 | 0,0174 | 6731,25 |
| 5 | 0,18 | 0,0324 | 0,35 | 0,0343 | 6764 |
Из таблицы находим Т* = minT = 500.
3. Критерий предельного уровня
Этот критерий не дает оптимального решения, а соответствует определению приемлемого способа действий.
Пример 3. Пусть величина спроса x на некоторый товар задается непрерывной функцией распределения Fx(x).
Если запасы в начальный момент не велики, в дальнейшем возможен дефицит. В противном случае к концу рассматриваемого периода запасы нереализованного товара могут оказаться очень большими. Человек, который принимает решение, может установить необходимый уровень запаса таким образом, чтобы величина ожидаемого дефицита не больше А1, а величина излишков не превосходила А2.
 Необходимый уровень запаса I определяется следующим образом:
Необходимый уровень запаса I определяется следующим образом:
 Пример 4. Пусть
Пример 4. Пусть
 Тогда
Тогда
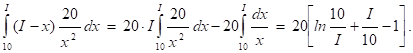 |
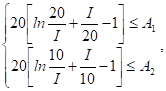 | |||||
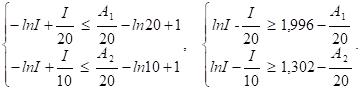 | |||||
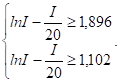 |
Пусть A1 = 2, A2 = 4. Тогда:
Ответ: I Î [10; 20].
4. Критерий наиболее вероятного исхода
Этот критерий основан на преобразовании случайной ситуации в детерминированную путем замены случайной величины единственным значением, имеющим наибольшую вероятность реализации.
Допустим, имеется изделие j и доход Cj. Pj – вероятность того, что доход принимает это значение Pj = P(C=Cj).
 Критерий говорит, что надо выбрать такое значение Cj*, чтобы
Критерий говорит, что надо выбрать такое значение Cj*, чтобы
Задачи к § 13
13.1. В производственном процессе партии товаров, имеющие 8%, 10%, 12% и 14% брака выпускаются с вероятностью 0,4; 0,3; 0,25; и 0,05 соответственно. Производитель связан контрактами с тремя потребителями. В них оговорено, что процент брака в партиях, направляемых потребителям А, В и С не должен превышать 8%, 12% и 14% соответственно. Если процент брака превышает обусловленного, то штраф составляет 100 долларов за 1% превышения. С другой стороны производство партии более высокого качества, чем требуемое, приводит к увеличению затрат производителя на 50 долларов за 1%. Кто из потребителей будет иметь наибольший приоритет при выполнении заказа, если партия не проверяется перед отправкой?
13.2. Спрос на некоторое изделие описывается следующей таблицей распределения:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,1 | 0,15 | 0,4 | 0,15 | 0,1 | 0,1 |
Определить уровень запасов, при котором вероятность полного истощения запасов не превышает 0,45.
Определите также уровень запасов при условии, что среднее значение дефицита и превышения запаса не должны быть выше 1 и 2 единиц соответственно.
 13.3. Автомат производит a тысяч единиц некоторого продукта ежедневно. Если a увеличивается, доля брака p возрастает. Плотность распределения случайной величины p дается следующей формулой:
13.3. Автомат производит a тысяч единиц некоторого продукта ежедневно. Если a увеличивается, доля брака p возрастает. Плотность распределения случайной величины p дается следующей формулой:
Каждое бракованное изделие приносит убыток в 50 долларов. Годное изделие дает прибыль 5 долларов.
Определите, при каком a ожидаемая прибыль принимает максимальное значение. Примените критерий ожидаемое значение – дисперсия. Сравните оптимальные решения для значение показателя несклонности к риску k = 1, 2, 5.
§ 14. Игры с ненулевой суммой
Пусть имеются два игрока и рассматривается матрица выигрышей каждого игрока в отдельности. Эти матрицы совмещают в одну, и полученную матрицу называют матрицей игры (а саму игру называют биматричной игрой).
Пример 1. Пусть А1 – матрица выигрышей первого игрока, А2 – матрица выигрышей второго игрока.
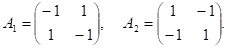 |
 Тогда совместная матрица игры С будет выглядеть следующим образом:
Тогда совместная матрица игры С будет выглядеть следующим образом:
Игры с ненулевой суммой делятся на:
- некооперативные (игроки не могут договориться);
- кооперативные (игроки согласовывают свои действия перед игрой).
А. Некооперативные игры
В играх с ненулевой суммой два игрока могут выигрывать и проигрывать одновременно. В некооперативных (или бескоалиционных) играх игроки принимают решения независимо друг от друга. Решение некооперативных игр основывается на нахождении точек равновесия игры.
Пусть
 - матрицы выигрышей первого и второго игрока соответственно.
- матрицы выигрышей первого и второго игрока соответственно.
Матрица игры выглядит так:
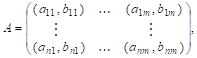
и пусть (x*, y*) – точка равновесия.
Тогда средние выигрыши первого и второго игрока будут равны, соответственно:
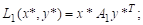
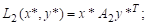
Определение 1. Точка (x*, y*) – точка равновесия по Нэшу, если выполняются следующие условия:
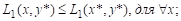
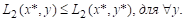
Ни одному из игроков не выгодно отклоняться от стратегии точки равновесия, если второй придерживается этой стратегии.
Приведем без доказательства следующую теорему.
Теорема Нэша. Каждая биматричная игра имеет по крайней мере одну точку равновесия. В общем случае равновесие может быть не единственным и каждому из них могут соответствовать различные значения выигрыша каждого из игроков.
Для игры 2×2 достаточными условиями для нахождения точки равновесия по Нэшу будут являться следующие неравенства:

 ,
,
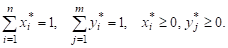
Рассмотрим несколько примеров
Пример 1 (Дилемма заключенных).
Два преступника ожидают приговора суда за совершенное преступление. Адвокат конфиденциально предлагает каждому из них облегчить их участь, даже освободить, если он сознается и даст показания против сообщника, которому в этом случае грозит тюремное заключение сроком на 10 лет. Если никто не сознается, то обоим угрожает заключение в один год по обвинению в незначительном преступлении. Если сознаются оба, то, с учетом чистосердечного признания, обоим грозит срок 5 лет.
Каждый игрок имеет две стратегии:
δ1 = {сознаться}; θ1 = {сознаться};
δ2 = {не сознаться}; θ2 = {не сознаться}.
Составим матрицу выигрышей игроков:
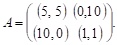
Выделим матрицы А1, А2 – матрицы выигрышей первого и второго игроков соответственно.
 ;
;  .
.
Найдём точку равновесия. Пусть x = (x1, 1-x1); y = (y1, 1-y1). Вычислим
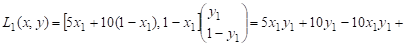
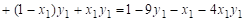
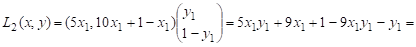
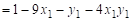
Для точки равновесия имеет место
имеет место
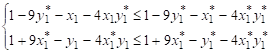
 , отсюда
, отсюда  .
.
Находим решение системы геометрически (4 системы).
Нужно найти такую точку, чтобы координаты удовлетворяли неравенствам: 
 .
.
Эта точка  (Проверьте самостоятельно). Тогда, пара стратегий по Нэшу выглядит так
(Проверьте самостоятельно). Тогда, пара стратегий по Нэшу выглядит так  .
.
Б. Кооперативные игры
Напомним еще раз, что кооперативной игрой называется игра с ненулевой суммой, в которой игрокам разрешается перед игрой обсуждать свои стратегии и договариваться о совместных действиях. Основная цель в этой игре – дележ общего выигрыша между членами коалиции.
Рассмотрим сначала кооперативную игру двух лиц на примере.
Пример 2. Пусть дана матрица кооперативной игры
 .
.
 Отметим на координатной плоскости (рис.1) точки,, соответствующие каждому элементу матрицы C ( их 4).
Отметим на координатной плоскости (рис.1) точки,, соответствующие каждому элементу матрицы C ( их 4).
Рис.1
Отмечаем также точку Т = (T1,T2) – точку угрозы, где T1, T2 – выигрыши игроков без вступления в коалицию. В нашем примере Т = (1, 1).
Северо-восточная граница области называется Парето-оптимальным множеством. Та часть Парето-оптимального множества, которая находится выше и правее точки угрозы называется переговорным множеством.
В данном случае Парето-оптимальное множество совпадает с переговорным множеством (АВ).
Вообще говоря, при решении кооперативной игры достаточно ограничиться нахождением переговорного множества. Однако, здесь мы также можем указать точку равновесия по Нэшу. Для этого обозначим
ƒ(L1,L2) = (L1 - T1)( L2 – T2)
 Точка равновесия по Нэшу удовлетворяет условию:
Точка равновесия по Нэшу удовлетворяет условию:
Найдем наибольшее значение функции на АВ. Из уравнения прямой АВ - L1 + L2 = 5 выразим L2 = 5 – L1 и подставим в:
f(L1) = (L1 – 1)(5 – L1 – 1) = ![]() , и найдем наибольшее значение функции одной переменной на отрезке:
, и найдем наибольшее значение функции одной переменной на отрезке:
![]() . Отсюда,
. Отсюда, ![]() = 2,5;
= 2,5; ![]() = 2,5.
= 2,5.
Это те значения, которые максимизируют функцию ƒ(L1,L2) в переговорном множестве. На рис.1 точка N = (2,5; 2,5) – точка равновесия по Нэшу.
Затронем теперь общие вопросы кооперативных игр.
Предположим, что имеется множество игроков N = {1, ¼, n}. K – некоторое подмножество K Ì N, состоящее из r £ n игроков.
 - число возможных коалиций игроков, договаривающихся о совместных действиях.
- число возможных коалиций игроков, договаривающихся о совместных действиях.
Определение 1. Функция V , ставящая в соответствии каждой коалиции K наибольший выигрыш, называется характеристической функцией игры.
Определение 2. Характеристическая функция V(K) называется простой, если она принимает два значения: 0 и 1.
Определение 3. Если характеристическая функция V простая, то коалиции K, для которых V(K) = 1 называются выигрывающими, а для которых V(K) = 0 – проигрывающими.
Свойства характеристической функции.
1) персональность (коалиция, не содержащая ни одного игрока, ничего не выигрывает).
V(Æ) = 0.
2) супераддитивность
V(KÈL) ³ V(K) +V(L), K,LÌ N, KÇL = Æ.
3) дополнительность
V(K) + V(N K) = V(N).
Обозначим через Xi выигрыш i-го игрока. И рассмотрим следующие два условия:
1) индивидуальная рациональность
Xi ³ V(i), iÎN.
2)  коллективная рациональность
коллективная рациональность
Определение 4. Вектор выигрышей X = (X1, ¼, Xn), удовлетворяющий условиям 1 и 2, называется дележом в условиях характеристической функции V.
Определение 5. Множество {N, V}, удовлетворяющее условиям 1 и 2, называется классической кооперативной игрой.
 Теорема 1. Для того, чтобы X = (X1, ¼, Xn) был дележом в классической кооперативной игре, необходимо и достаточно, чтобы
Теорема 1. Для того, чтобы X = (X1, ¼, Xn) был дележом в классической кооперативной игре, необходимо и достаточно, чтобы
Определение 6. Кооперативные игры называются существенными, если для любых коалиций K и L выполняется неравенство: V(K) +V(L) < V(KÈL).
Если выполняется равенство V(K) + V(L) = V(KÈL), то такая игра называется несущественной.
Рассмотрим следующие свойства:
 1) для того, чтобы характеристическая функция V была аддитивной (кооперативная игра несущественной), необходимо и достаточно выполнения следующего равенства:
1) для того, чтобы характеристическая функция V была аддитивной (кооперативная игра несущественной), необходимо и достаточно выполнения следующего равенства:
2) в несущественной игре имеется только один дележ:
{V(1), V(2), ¼, V(n)}.
3)  в существенной игре более чем одним игроком множество дележей бесконечно:
в существенной игре более чем одним игроком множество дележей бесконечно:
Определение 7. Пусть имеется два дележа
X = (X1, ¼, Xn), Y = (Y1, ¼, Yn)
и некоторая коалиция K.
 Тогда дележ X доминирует Y по коалиции K, если выполняются два условия:
Тогда дележ X доминирует Y по коалиции K, если выполняются два условия:
1) - эффективность доминирующего дележа,
2) Xi > Yi, iÎ K – свойство предпочтительности.
Соотношение доминирования возможно не по всякой коалиции. Например, невозможно доминирование по коалиции, состоящей из одного игрока или из всех игроков.
В любой несущественной игре имеется только один дележ, поэтому здесь доминирования нет.
Поскольку вариантов дележа много, необходимо выделить дележи, которые не доминируются никакими другими дележами. Такие дележи называются вполне устойчивыми, а множество таких дележей называется С-ядром.
Теорема 2. Для того, чтобы дележ X принадлежал С-ядру игры {N, V}, необходимо и достаточно, чтобы для любой коалиции K выполнялось неравенство
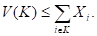 |
Замечания:
1) в несущественной игре С-ядро существует и состоит из единственного дележа этой игры;
2) во всякой существенной игре с постоянной суммой С-ядро пусто.
Дж.фон Нейман и О.Моргенштерн предложили следующее решение кооперативной игры.
Определение 8. Решением по Нейману-Моргенштерну кооперативной игры R называется множество дележей, удовлетворяющее условиям:
1) внутренняя устойчивость (дележи из решения нельзя противопоставить друг другу);
2) внешняя устойчивость (имеется возможность каждому отклонению от решения противопоставить некоторый дележ, принадлежащий решению).
Теорема 3. Если в кооперативной игре существует С-ядро С и решение R, то С < R.
Решение по Нейману-Моргенштерну обладает следующим свойством: решение кооперативной игры не может состоять только из одного дележа, так как в этом случае характеристическая функция игры – несущественная.
Решение по Нейману-Моргенштерну имеет ряд недостатков, которые сводятся к следующему: принцип оптимальности, приводящий к решению по Нейману, не является полным. Это означает, что он не в состоянии указать игрокам единственную систему норм распределения дележа.
Еще одним подходом к поиску решения кооперативной игры является подход Шепли, основанный на аксиомах, отражающих справедливость дележей игры.
Определение 9. Носителем игры с характеристической функцией V называется такая коалиция T, что для любой другой коалиции S выполняется следующее равенство:
V(S) = V(SÇT).
Т.е. любой игрок, не принадлежащий коалиции T, является нейтральным. Он не может ничего внести в коалицию и ему ничего не следует выделять из общих средств.
Предположим, что П - любая перестановка игроков множества N.
Через ПV = U обозначим характеристическую функцию такой игры, что для коалиции S = {i1, ¼, iS} имеет место следующее:
U(П(i1), ¼, П(iS)) = V(S).
Аксиомы Шепли.
1) Эффективность.
 Если S – любой носитель игры {N, V}, то
Если S – любой носитель игры {N, V}, то
При разделении общего выигрыша носителя игры ничего не выделять на долю посторонних.
2) Симметрия.
 Для любой перестановки П и iÎ N, выполняется следующее:
Для любой перестановки П и iÎ N, выполняется следующее:
Игроки, одинаково входящие в игру, должны получать одинаковые выигрыши.
3) Агрегация.
Если есть две игры с характеристическими функциями V/ и V//, то
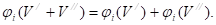 |
При участии игроков в двух играх, их выигрыши в отдельных играх должны складываться.
 Определение 10. Вектором цен (вектором Шепли) игры с характеристической функцией V называется n-мерный вектор
Определение 10. Вектором цен (вектором Шепли) игры с характеристической функцией V называется n-мерный вектор
удовлетворяющий аксиомам Шепли.
Терема 4. (Шепли) Существует единственная функция j, определенная для всех игр, и удовлетворяющая аксиомам Шепли.
 Определение 11. Характеристическая функция WS(T), определенная для любой коалиции S называется простейшей, если
Определение 11. Характеристическая функция WS(T), определенная для любой коалиции S называется простейшей, если
Пусть ji(V) – компоненты вектора Шепли, t – число элементов множества T.
 Тогда
Тогда
 Вектор Шепли интерпретируется следующим образом: предельная величина, которую вносит i-ый игрок в коалицию T, выражается V(T) – V(T{i}), и считается выигрышем i-го игрока. Если обозначим через gi(T) вероятность того, что i-ый игрок вступит в коалицию, то выигрыш i-го игрока составит:
Вектор Шепли интерпретируется следующим образом: предельная величина, которую вносит i-ый игрок в коалицию T, выражается V(T) – V(T{i}), и считается выигрышем i-го игрока. Если обозначим через gi(T) вероятность того, что i-ый игрок вступит в коалицию, то выигрыш i-го игрока составит:
Суммирование ведется по всем выигрывающим коалициям T, при условии, что коалиция T{i} не является выигрывающей.
Пример. Рассмотрим корпорацию из четырех акционеров, имеющих акции в количествах: а1=10; а2=20; а3=30; а4=40. Предположим, что любое решение утверждается акционерами, имеющими в сумме большинство акций, и это решение считается выигрышем, равным 1. Данную ситуацию можем рассмотреть как игру четырёх участников, в которой выигрывающими будут следующие коалиции:
 .
.
Определим компоненты вектора Шепли. При нахождении  учтем, что имеется только одна коалиция T={1; 2; 3}, которая выигрывает, а коалиция T{1} = {2; 3} не выигрывает. В этой коалиции имеется три игрока, т.е. t = 3, поэтому
учтем, что имеется только одна коалиция T={1; 2; 3}, которая выигрывает, а коалиция T{1} = {2; 3} не выигрывает. В этой коалиции имеется три игрока, т.е. t = 3, поэтому
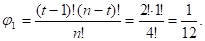
Теперь определим все выигрывающие коалиции, но не выигрывающие без второго игрока. Таких коалиций три: {2; 4}, {1; 2; 3}, {2; 3; 4}. Поэтому  .
.
Аналогично получаем, что  . Таким образом, вектор Шепли выглядит так:
. Таким образом, вектор Шепли выглядит так:  .
.
Замечание. Если считать, что вес голоса акционера пропорционален количеству имеющихся у него акций, то получим вектор голосования (0,1; 0,2; 0,3; 0,4), который, как видно, отличается от вектора Шепли.
Задачи к § 14
14.1. Пусть студент предполагает сдать зачет преподавателю. Чтобы получить зачет студент должен правильно ответить хотя бы на два из трех предложенных вопросов. Сформулируйте задачу как игру с ненулевой суммой, найдите решение.
14.2. На просмотр фильма в кинотеатре школьникам выдали билеты. Количество билетов ограничено. На два класса администрация выделила 60 билетов, но впереди контрольная по математике, и администрация решила учесть результаты контрольной. Если один из классов пишет без троек, то он получает 60 билетов. Если два класса не получают тройки, то каждый получит по 30 билетов. Если ни один из классов не пишет без троек, то они получают по 15 билетов. Сформулируйте задачу как игру с ненулевой суммой, найдите решение.
14.3. Пяти предпринимателям предложили проинвестировать проект, стоимость которого составляет $1100 . У предпринимателей имеются $200, $300, $500, $600 и $800, соответственно. Проект отдадут тем предпринимателям, у которых будет необходимая сумма для его финансирования. Найти вектор Шепли.
14.4. Инвесторы решают вопрос о направлении средств в те или иные отрасли страны N. После дискуссий основная масса инвесторов решила из множества вариантов вложений выбрать три наиболее привлекательных и обсудить их отдельно. Одновременно с этим обсуждением правительство на своем заседании рассматривает несколько альтернативных стратетий развития экономики на ближайшие несколько лет. Инвесторы стоят перед выбором между инвестициями в нефтедобывающую, лесоперерабатывающую, автомобилестроительную отрасли. В одно и то же время с их закрытым совещанием происходит закрытое заседание правительства, на котором оно должно сделать выбор между преимущественным развитием нефтедобычи, железных дорог, электроэнергетики или жилищного комплекса. Сформулируйте задачу как игру с ненулевой суммой, составлением матрицы игры.
14.5. У торговой фирмы есть две грузовые машины, которые возвращаются из разных городов. Фирме требуется срочно отправить груз в город N. Если водители приедут точно по графику или раньше, и отправяться в срочную командировку, то у каждого из них будет простой в два дня. Если оба водителя опоздают, то у них будет по одному дню простоя. Если один из них приедет вовремя или раньше и отправиться в город N, то у него не будет простоя, а у другого будет простой в пять дня. Сформулируйте задачу как игру с ненулевой суммой, найдите решение.
§ 15. Многоэтапный процесс принятия решений
Рассмотрим игру, в которой игроки принимают решения поочередно, зная о том, какую стратегию в предыдущем шаге применил противник. Такие игры также называют позиционными играми. Анализ такой игры проведем на примере.
Пример. Фирма (первый игрок) может принять решение о строительстве крупного или небольшого предприятия. Небольшое предприятие впоследствии можно расширить. Решение определяется будущим спросом. Если спрос на продукцию большой, то строится крупное предприятие.
 Условие задачи представлено в виде так называемого «дерева решений»:
Условие задачи представлено в виде так называемого «дерева решений»:

 где
где - решающие вершины, т.е те вершины, где первый игрок принимает решение, - случайные вершины.
- решающие вершины, т.е те вершины, где первый игрок принимает решение, - случайные вершины.
Определим действия предприятия на 10 лет. Сначала определим, какое решение примет первый игрок в решающей вершине 4, а затем в вершине 1. Для этого вычислим средние величины прибыли (обозначим через X) в вершине 4 при расширении и без расширения.
При расширении:
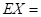
 ;
;
без расширения:
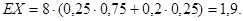
Поскольку, ожидаемая чистая прибыль без расширения больше, то в вершине 4 выгоднее не проводить расширения. Считая, что за последние восемь лет при этом мы получим чистую прибыль, равную $1,9 млн. мы переходим к вершине 1.
При строительстве крупного предприятия чистая прибыль составит:
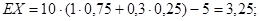
а при строительстве небольшого предприятия:
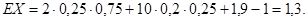
Сравнив полученные значения прибыли, мы приходим к выводу, что оптимальным решением в вершине 1 является решение о строительстве крупного предприятия.
Задачи к § 15
15.1. Изменим условия примера, рассмотренного в § 15 следующим образом. Имеется три вида спроса: высокий (с вероятностью 0,6), средний (0,3) и низкий (0,1). При переходе предприятия из состояния «3» в состояние «4» при высоком спросе ежегодный доход составляет $300 тыс. Годовые доходы составляют:
состояние «2» - высокий спрос – $1млн.,
- средний спрос – $400 тыс.,
- низкий спрос – $200 тыс.,
состояние «5» – высокий спрос – $900 тыс.,
- средний спрос – $400 тыс.,
- низкий спрос – $200 тыс.,
состояние «6» – высокий спрос – $300 тыс.,
- средний спрос – $250 тыс.,
"Инструмент для проведения спускоподъемных операций" - тут тоже много полезного для Вас.
- низкий спрос – $200 тыс.,
состояние «3» – средний спрос – $250 тыс.,
- низкий спрос – $200 тыс.
Требуется составить дерево решений и определить действия предприятия.
15.2. В рамках задачи 15.1 допустим вероятности высокого и низкого спроса неизвестны. Какова должна быть вероятность высокого спроса, чтобы фирме было выгодно строить небольшое предприятие.
15.3. В рамках задачи 15.2 подобрать вероятности низкого и среднего спроса, чтобы выгодно было строить крупное предприятие.


 T
T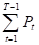
 T
T , и найдем наибольшее значение функции одной переменной на отрезке:
, и найдем наибольшее значение функции одной переменной на отрезке: . Отсюда,
. Отсюда,  = 2,5;
= 2,5;  = 2,5.
= 2,5. 



















