Фрактальные агрегаты
ГЛАВА II. Фрактальные агрегаты
Большая часть окружающего нас мира состоит из нерегулярных объектов, построенных полностью необратимым путем. Образование деревьев, гор, рек являются достаточно общими примерами. Со времени введения концепции фракталов произошел некоторый прогресс в описании таких нерегулярных структур. Однако недостаточно только описывать нерегулярные формы, необходимо также понять внутренний механизм, который приводит к ним.
Фрактальный агрегат (или фрактальный кластер) – это система, образующаяся из твердых частиц в процессе их слипания, один из типов кластеров с фрактальной структурой. Обычно кластером называют большое число связанных атомов или молекул, которые внутри этой системы сохраняют свою индивидуальность, однако, этот термин распространился и на системы, состоящие из большого числа связанных макроскопических частиц.
Такие агрегаты образуются и растворе при образовании геля, т. е., кластера, состоящего из соединенных частиц – золей, при образовании пленок на поверхности тела, находящегося в контакте со средой, содержащей аэрозоли и т. д. Тем самым фрактальный кластер (агрегат) образуется в процессах роста кластера при слипании твердых частиц, соединение которых происходит по определенному закону. Структура и свойства фрактальных кластеров определяется физической природой процессов, протекающих при его образовании. Можно сказать и по-другому: рост фрактального кластера аналогичен ряду физических процессов и структур; аналогии этих процессов и структур состоят в том, что при некоторых условиях они имеют одинаковое математическое описание.
КОЛИЧЕСТВЕННОЕ ОПИСАНИЕ ФРАКТАЛЬНЫХ
АГРЕГАТОВ
Детерминированные фрактальные агрегаты
Рассмотрим построение агрегата в соответствии с детерминированным правилом. Этот агрегат конструируется путем последовательного соединения идентичных сферических частиц радиуса а следующим образом. Начальная частица располагается в начале прямоугольной системы координат. Шесть других частиц присоединяются к ней, двигаясь вдоль положительных и отрицательных направлений трех базисных векторов. Зaтем этот ансамбль из семи частиц рассматривается как начальный: шесть таких же ансамблей присоединяются к его концам и процедура повторяется. Легко показать, что после р итераций возникает агрегат, содержащий N = 7p частиц в сфере радиуса R = Зра.
Рассмотрим аналогичный, но бóльший агрегат, построенный после большого числа итераций. Этот агрегат содержит n(r) частиц, находящихся в сфере радиуса r с центром в начале координат. Так как r = ЗPа и n(r) = 7Р, то между этими величинами существует связь n(r) = ArD, где А = a -D и D = ln7/ln5 = 1,7712.
Рекомендуемые материалы
Фрактальная размерность кластеров
Обычно, если такое соотношение справедливо, считается, что этот объект – фрактал, a D – фрактальная размерность. D показывает, как масса распределена в пространстве. Для плотно расположенных сфер в d-мерном евклидовом пространстве D = d. Для выстроенных в линию сфер в любом пространстве размерности d > 1, D = 1 и т. д. Таким образом, вышеприведенное определение D совпадает с обычным определением размерности для гладких структур.
Обычно для агрегатов, построенных с помощью цепочек сфер (без перекрытия), фрактальная размерность  В вышеприведенном примере D нецелое число и лежит между 1 и 3 (3 в данном случае – размерность пространства вложения). Вернемся к примеру и вычислим плотность материи, содержащейся в сфере радиуса r с центром в начале координат. Предполагая, что каждая сфера – единичной массы, для плотности р (r) получим
В вышеприведенном примере D нецелое число и лежит между 1 и 3 (3 в данном случае – размерность пространства вложения). Вернемся к примеру и вычислим плотность материи, содержащейся в сфере радиуса r с центром в начале координат. Предполагая, что каждая сфера – единичной массы, для плотности р (r) получим
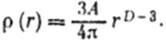
Обычно для фракталов размерности D, построенных в d-мерном пространстве, 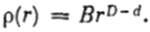
Это также справедливо для сфер с центром в r0 от начала координат, если r >> r0. Таким образом, для фрактальных агрегатов с D < d, чем больше размер сферы, окружающей частицу, тем меньше плотность материи в ней. Это означает, что, рассматривая всё большие и большие части фрактала, учитывают всё большие и большие пустоты. Другими словами, фрактал должен содержать пустоты всех размеров. Величина ρ(r) – это так называемая двухчастичная корреляционная функция: для данной частицы эта функция дает вероятность найти другую частицу на расстоянии r от первой. Таким образом, для фрактала корреляционная функция уменьшается по степенному закону от расстояния ρ ≈ r -a, а фрактальная размерность D непосредственно входит в экспоненту.
Сравним фрактал с перколяционным кластером, объектом, имеющим отношение к другим физическим процессам (см. главу 3).
Рассмотрим простейшую модель построения перколяционного кластера. Возьмем кубическую решетку и соединим некоторые из соседних узлов решетки. Из этих соединительных линий и состоит перколяционный кластер. Введен вероятность р того, что соседние узлы решетки связаны так, что 1-р представляет собой вероятность того, что соседние узлы не соединены. Из связанных таким образом областей получим кластеры, обладающие фрактальной структурой. По мере роста вероятности р характерные размеры таких кластеров растут, и при некотором значении р = рс образуется бесконечный кластер, что существенно в процессах переноса.
Этот кластер обладает фрактальными свойствами, однако, можно отметить его принципиальное отличие от фрактального кластера, образующегося в процессах роста. Для фрактального кластера его средняя плотность ρ падает по мере увеличения его размера R в соответствии с формулой ρ ~ RD-d, где d – размерность пространства, D – фрактальная размерность кластера. Поэтому плотность фрактального кластера бесконечных размеров стремится к нулю. Что касается перколяционного кластера, то он может стать бесконечным только при условии, что его плотность превышает некоторую критическую величину. Столь принципиальное отличие свойств этих кластеров отражает различие физических процессов, которые они описывают.
Естественные ограничивающие масштабы
Если бы фрактальные агрегаты были бесконечно большие и сделаны из бесконечно малых отдельных частиц, то не было бы никаких ограничений на свойства, описанные выше. Практически существуют два естественных (нижний и верхний) масштаба обрезания: размер отдельных частиц, а, и размер самого агрегата L. Обычно свойство n (r) ~ rD справедливо только при a<<r<<L. Это показывает различие между математическими фрактальными объектами (без ограничений) и физическими фракталами. Моделирование реальных агрегатов фрактальными структурами оправдано, если эти два масштаба обрезания достаточно хорошо разделены, т. е., практически, если агрегат достаточно большой (отношение L/a должно быть больше 10).
Случайные фракталы
Если в детерминированный способ построения агрегатов включить некоторый элемент случайности, как это бывает во многих естественных процессах роста, то можно построить случайные фракталы. Хорошо известный пример – это траектория движения брауновской частицы, которая имеет фрактальную размерность, равную двум (размер траектории изменяется как корень квадратный из ее длины). Основное отличие от детерминированных фракталов состоит в том, что вышеприведенные правила в данном случае справедливы только после соответствующего усреднения по всем статистически независимым реализациям объекта.
Экспериментальные методы измерения
фрактальной размерности
Основным непосредственным методом вычисления фрактальной размерности агрегата является количественный анализ (в соответствии с определением фрактальной размерности) микрофотографий объекта.
Если имеется большое число агрегатов разных размеров и есть убедительные причины считать, что они имеют одинаковую фрактальную размерность (успех метода служит хорошим тестом), то следует просто изобразить общую интенсивность как функцию характерного размера каждого агрегата. Этот размер может быть радиусом вращения объекта, или, более просто, радиусом наименьшей окружности или сферы, содержащей агрегат. Наклон этой кривой в логарифмических координатах дает фрактальную размерность. Это, конечно, лучший метод, если имеется достаточно большой набор агрегатов, чтобы уменьшить статистический разброс.
АГРЕГАЦИОННЫЕ МОДЕЛИ ЧАСТИЦА-КЛАСТЕР
Ограниченная диффузией агрегация частица-кластер
Пионерская модель была создана Томасом Виттеном и Леонардом Сэндером. В этой модели частицы добавляются одна за другой к одному растущему кластеру. В первоначальной версии агрегационный процесс возникает от неподвижной начальной частицы. Затем агрегат растет. На каждом шаге движущаяся частица стартует из случайно выбранной точки на большой окружности с центром в зародыше и совершает чисто хаотическое движение в пространстве до встречи с агрегатом (средняя длина пути такого диффузионного движения условно равна диаметру частицы). После первого столкновения частица считается жестко приклеенной к агрегату в месте соударения, затем другая частица стартует с окружности и т. д. Если движущаяся частица диффундирует слишком далеко от агрегата (как типичное, это расстояние в три раза больше радиуса большого круга), она выбывает из игры, и стартует другая частица (причина этого состоит в том, что вероятность для такой частицы вновь вернуться па окружность становится равномерно распределенной по ее длине).
Компьютерное моделирование такого подхода было впервые проделано на двумерной квадратной решетке. Затем эти вычисления были развиты для различных других решеток, более высоких размерностей, исследовался также ряд нерешеточных версий.
До недавнего времени обычно считалось, что виттен-сэндеровские агрегаты – простые самоповторяющиеся структуры, фрактальная размерность которых не зависит от природы базовой решетки и определяется только размерностью пространства вложения. Вычисленные фрактальные размерности виттен-сэндеровской модели как функция размерности пространства d приведены в таблице.
| d | 2 | 3 | 4 | 5 | 6 |
| D | 1,70 | 2,50 | 3,33 | 4,20 | 5,3 |
Аналитические исследования, подтвержденные компьютерным моделированием (более чем 106 частиц), показывают, что виттен-сэндеровские агрегаты являются специальным видом самоаффинных фракталов с фрактальной размерностью, большей в радиальном направлении (среднее направление роста), чем в тангенциальном направлении (перпендикулярно среднему направлению роста), и что фрактальные размерности зависят от типа решетки.
В термодинамическом пределе бесконечно большого агрегата структура должна образовать, звезду, сформированную из конечного числа бесконечно тонких иголок; число иголок зависит от типа решетки (4 для квадратной, 6 для треугольной и т. д.). В нерешеточном случае среднее число ветвей должно быть между 4 и 6. Из этих данных следует, что виттен-сэндеровская модель не обладает свойством универсальности, хорошо известным в статистической физике, которое требует, чтобы характеристические экспоненты не зависели от микроскопических деталей – таких, как природа базовой решетки. Такое нарушение универсальных свойств является следствием необратимого характера модели.
Экспериментальные реализации виттен-сэндеровской модели
Виттен-сэндеровская модель, в которой движутся только отдельные частицы, неадекватно моделирует регулярные, или собственно-агрегационные эксперименты (где все кластеры движутся), которые проводятся на аэрозолях или коллоидах. Тем не менее эта модель хорошо применима для изучения агрегационных явлений, вызванных внешними полями, где, в дополнение к межчастичному взаимодействию, существует внешнее поле, которое приводит к взаимодействию частицы и агрегата.
Виттен-сэндеровская модель является достаточно общей и используется для описания многих процессов роста.
Отметим, что при применении к агрегационным экспериментам виттен-сэндеровская модель имеет большое неудобство, так как в ней невозможно никакие структурные изменения агрегата в течение процесса. Частица остается жестко фиксированной в точке соприкосновения и не может достичь другой, более выгодной позиции с меньшей общей энергией. В частности, эта модель не может быть непосредственно применена для описания кристаллического роста дендритов, где хорошо известно, что существуют анизотропные эффекты, поверхностное натяжение, поверхностная диффузия. Были развиты некоторые обещающие расширения виттен-сэндеровской модели, включающие внутренние анизотропные параметры, так же как и возможность частичной реконструкции. Эти исследования позволяю нам двигаться непрерывно от нерегулярных фрактальных форм к боле регулярным и периодическим структурам (например, наблюдаемым в снежинках).
Другие частица-кластерные модели
Установлено, что брауновская природа траектории частицы является существенной для воспроизведения фрактальной структуры. Все другие частица-кластерные модели, где частицы движутся по прямым траекториям, дают компактные (D = d) агрегаты.
Так называемая баллистическая модель, в которой частицы движутся по случайным линиям в пространстве, была введена М. Волдом и Д. Саферлендом. Считалось, на основе численных результатов, что баллистические агрегаты могут быть фрактальными, но более эффективные недавние машинные эксперименты совместно с аналитическими аргументами определенно установили их компактный характер.
В так называемой модели дождя рассматриваются случайные прямые линии без параметров соударения, т. е., всегда проходящие через зародыш агрегата. Кластеры снова компактны, даже с много большей плотностью.
Пауль Мекин ввел обобщенную модель, рассматривающую фрактальные траектории с меняющейся фрактальной размерностью dw. Для dw = 2 получается виттен-сэндеровская модель. Также найдено, что фрактальная размерность увеличивается, когда dw уменьшается до единицы (баллистическая модель), ниже которой остается постоянной и равной размерности пространства. Была построена другая интерполяционная модель между брауновским и баллистическим случаем, в которой длина свободного пробега при диффузии частицы может меняться по сравнению с диаметром частицы.
В этом случае наблюдается типичный переходный эффект. Для конечной длины свободного пробега, большей диаметра частицы, сначала наблюдается промежуточный режим роста, и котором агрегат, очевидно, более компактен; но, достигнув достаточно большого размера, он становится похож на виттен-сэндеровский агрегат. Баллистическая модель возникает только в пределе, когда длина свободного пробега стремится к бесконечности и всегда больше размера агрегата.
Другая очень простая частица-кластерная модель, в которой не рассматриваются какие-либо траектории вообще, – модель М. Айдена, которая была введена для изучения роста опухоли. В этой модели на каждой итерации новая частица присоединяется с равной вероятностью случайно на одно из возможных мест на поверхности. Эта модель может рассматриваться как предел dw = 0, обобщенной модели, определенной выше, приводит также к очень компактным структурам. Однако если объемные свойства как баллистической, так и айденовской моделей тривиальны, их поверхности проявляют интересные несовершенства, которые сейчас активно изучаются.
КЛАСТЕР-КЛАСТЕРНЫЕ МОДЕЛИ АГРЕГАТОВ
Кластер-кластерные агрегаты, ограниченные диффузией
С тех пор как была создана виттен-сэндеровская модель, стало понятно, что она не является наиболее приемлемой моделью-агрегационных экспериментов па коллоидах и аэрозолях. Теоретические значения фрактальвых размерностей (D ≈ 2,5) были слишком большими по сравнению с экспериментальными (D ≈ 1,7). Чтобы лучше описать эти эксперименты, была предложена альтернативная кластер-кластерная.
Эта модель может рассматриваться как расширение виттен-сэндеровской модели, в которой сами кластеры могут двигаться вместе с частицами. В первоначальной версии модель стартовала с набора идентичных сферических частиц, случайно распределенных внутри замкнутого куба. Затем эти частицы начинали диффундировать в пространстве (аналогично случайным блужданиям на решетке в виттен-сэндеровском случае). На границе куба задавались периодические граничные условия. Когда две частицы сталкивались, они необратимым образом соединялись вместе в форме твердого димера, который также мог диффундировать внутри куба, сохраняя свою ориентацию. Он мог соединиться с другим димером или отдельной частицей и т. д. После каждого столкновения два сталкивающихся кластера образуют новый больший кластер. Процедура может продолжаться до тех пор, пока в кубе останется лишь один агрегат.
В кластер-кластерной модели вводится параметр α, чтобы описать, как скорость кластера изменяется в зависимости от числа частиц i, принадлежащих ему υi ≈ iα.
Для реалистичных случаев достаточно отрицательных величин α, т. о., когда маленькие кластеры движутся быстрее, чем большие, и в предельном случае бесконечно малой начальной концентрации частиц было установлено, что все агрегаты являются фракталами и их фрактальная размерность не зависит от α в большом диапазоне изменения этой величины. Фрактальная размерность зависит только от размерности пространства и существенно меньше, чем в виттен-сэндеровской модели.
Проведено систематическое изучение влияния начальной концентрации частиц, показывающее эффективное увеличение фрактальной размерности с концентрацией. Кластер-кластерная модель с высокой концентрацией предложена как модель переходов, наблюдаемых в полимерных растворах.
Иерархическая модель
Иерархическая модель – это идеализированная версия кластер-кластерной модели. В этой модели следующие один за другим наборы кластеров из равного числа части: 2, 4, 8, . . ., 2Р, . . ., строятся последовательно. На каждом шаге кластеры группируются парами и один из них может диффундировать в пространстве до соударения с другим. Эта версия концептуально много проще и дает такие же количественные результаты при меньшем компьютерном времени.
Эта версия привела к некоторым полезным аналитическим и численным исследованиям. В частности, было аналитически установлено, что, в отличие от частица-кластерной модели, в кластер-кластерной модели существует верхняя критическая размерность (d ≈ 9), выше которой кластеры становятся прозрачными друг для друга и, следовательно, их фрактальная размерность становится независимой от размерности пространства. В то же время были проделаны численные исследования до пространственной размерности, равной 6, и экстраполяция в большие размерности была в согласии с теоретическими предсказаниями. Было также проверено, что нет влияния базовой решетки, так как нерешеточная иерархическая версия дала такие же численные результаты. После усреднения по большому числу трехмерных нерешеточных агрегатов найдена фрактальная размерность D ≈ 1,8, очень близкая к полученной из экспериментов на коллоидах и аэрозолях.
С использованием иерархической версии были проверены слабые эффекты возможной вращательной диффузии. Было также обнаружено, что кластер-кластерные агрегаты были анизотропны и по существу имели в среднем эллипсоидальную форму. Систематическое изучение анизотропных свойств показывает, что отношение между наибольшим и наименьшим собственным значением радиуса вращения агрегата равно примерно пяти в d = 2 и десяти в d = 3. Однако такие эффекты, как наведенная анизотропия или зависимость от базовой решетки, никогда не наблюдались, в отличие от виттен-сэндеровской модели. В настоящее время считается, что кластер-кластерные агрегаты приводят к простым самоподобным случайным фрактальным структурам.
Влияние траектории кластера и химическая модель
Изучены некоторые расширения кластер-кластерной модели, в которых вводилась модификация траекторий. Баллистическая кластер-кластерная модель, которая рассматривает случайные прямолинейные траектории, хорошо иллюстрирует молекулярный режим аэрозолей. Показано, что такая модификация, в отличие от виттен-сэндеровской модели, только слегка увеличивает фрактальную размерность конечных агрегатов.
Чтобы учесть дальнодействующее притягивающее взаимодействие, можно также рассматривать прямолинейные траектории без параметров соударения. И снова фрактальная размерность лишь слегка увеличивается.
Другое расширение, которое является кластер-кластерным вариантом модели М. Айдена, полностью исключает роль траектории: в отличие от диффузионно ограниченной агрегации, это расширение было названо химически ограниченной кластер-кластерной агрегацией. При построении этой модели вводится понятие вероятности соединения, и затем эта вероятность устремляется к нулю. В этом пределе кластеры некоторое время «изучают» все возможные соединения и в конце концов выбирают одно случайное. Интерес к такой модели вызван тем, что она реализуется в коллоидах, когда, электростатическое отталкивание не полностью экранировано. Фрактальная размерность в этом случае равна D ~ 2 в d = 3 – немного, но все-таки больше, чем величина D ~ 1,78, полученная в чисто диффузионном случае (с вероятностью соединения равной единице). Такое изменение фрактальных свойств агрегатов явно наблюдалось Д. Вейцем с соавторами в экспериментах на золотых коллоидах, сразу же после появления химической модели.
Фрактальные размерности кластер-кластерной модели как функция пространственной размерности в случае брауновской, баллистической (случайные прямолинейные траектории) и химической версии этой модели и в случае линейных траекторий без параметра соударения приведены в таблице.
Существующие математические модели описывают возможные физические ситуации при агрегации частиц и кластер. В следующей таблице, приведенной ниже, представлены значения фрактальной размерности кластеров, образующихся в трехмерном пространстве при различных механизмах роста. Деление на разные способы роста кластера может быть проведено по следующим параметрам. Во-первых, кластер может расти за счет присоединения
| d | 2 | 3 | 4 | 5 | 6 |
| (dw = 2), брауновская (dw = 1), баллистическая Химическая Линейная (без параметра соударения) | 1,44 1,51 1,55 1,56 | 1,78 1,91 2,04 2,06 | 2,05 2,22 2,32 2,53 | 2,27 2,47 — 2,97 | 2,8 2,7 — 3,46 |
| Модель агрегации | Фрактальная размерность |
| Частица-кластер, прямолинейная траектория Частица-кластер, брауновское движение Кластер-кластер, прямолинейная траектория Кластер-кластер, брауновское движение Кластер-кластер, малая вероятность слипания | "33 Дисциплинарная ответственность" - тут тоже много полезного для Вас. 3,00 2,46±0,05 1,94±0,08 1,77±0,03 2,02±0,06 |
к нему отдельных частиц (агрегация кластер-частица), двух кластеров, которые, в свою очередь, являются результатом агрегации кластеров меньших размеров (кластер-кластерная агрегация). Во-вторых, объединяющиеся частицы или кластеры могут иметь разный характер движения в пространстве (брауновское или прямолинейное), а это отражается на компактности кластера. В-третьих, компактность образуемого кластера зависит от вероятности, с которой объединяются соприкасающиеся частицы. Чем меньше эта вероятность, том глубже внедряются частицы в кластер или кластер в кластер, т. е., тем более компактным является образуемый кластер.






















