Спектр дискретизированного (квантованного по времени) сигнала

Сигнал, дискретизированный с периодом T_s , можно представить как произведение непрерывной функции x(t) (а) и последовательности δ – функций x_δ(t) (в):

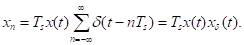
Спектр сигнала x_δ(t) – последовательность (г) гармоник, следующих с частотным интервалом 1/T_s  и имеющих одинаковые амплитуды, что следует из выражения для комплексной амплитуды С_n  спектра:

 

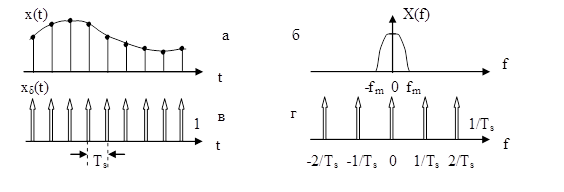
Если известен спектр (б) сигнала x(t), то спектр дискретизированного сигнала  x(t) получим заменой каждой линии спектра сигнала x_δ(t) спектральной функцией сигнала x(t):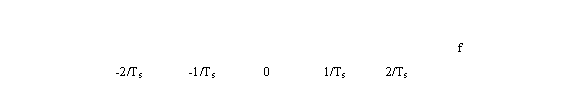

Спектр дискретизированного сигнала состоит из последовательности бесконечно повторяющихся, с частотой дискретизации  1/T_s , спектров исходного непрерывного сигнала.

Если 1/T_s>2f_m (выполняется условие Найквиста), наложения отдельных «лепестков» спектра нет, форма лепестка спектра сохраняется и исходный сигнал можно восстановить из дискретизированного сигнала без искажений.

Рекомендуемые материалы

Влияние диcкретизации на спектр сигнала поясняет пример: при частоте дискретизации 5 Гц сигнал частоты 6 Гц воспринимается как сигнал частоты 1 Гц.

Неправильный выбор частоты дискретизации может привести к ошибочным результатам и к полной неработоспособности системы.

При вычислении спектра на ЭВМ задают длительность сигнала τ  и шаг дискретизации Δt. ЭВМ вычисляет спектральную функцию с шагом по частоте Δf_min=1/ τ  и выдает один лепесток спектра шириной f_max =1/ Δt. На краю полосы f_max  спектр амплитуд должен быть близок к 0, иначе есть наложение лепестков спектра и необходимо уменьшить шаг дискретизации.  

Осциллограмма и спектр амплитудно-модулированного

сигнала с шумом

Информация в лекции "15 Острая гнойная инфекция костей" поможет Вам.

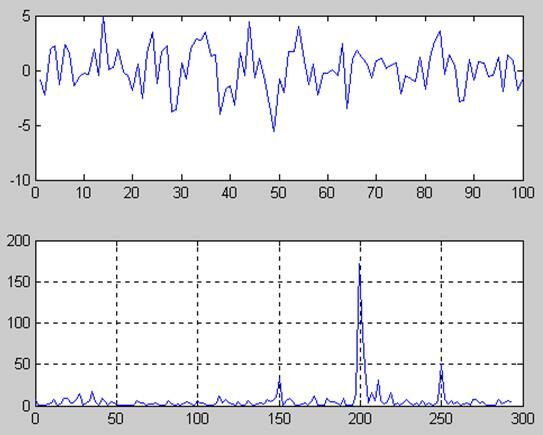 s(t)=sin400pt+0.4sin300pt+0.4sin500pt+2N(t)

Спектральный анализ  позволяет выделить все гармонические составляющие сигнала на фоне шумов и тем самым получить информацию об источнике сигнала. Чем короче сигнал по времени, тем ниже точность спектрального анализа.  Для повышения точности спектрального анализа кратковременных сигналов применяют специальные методы.

 

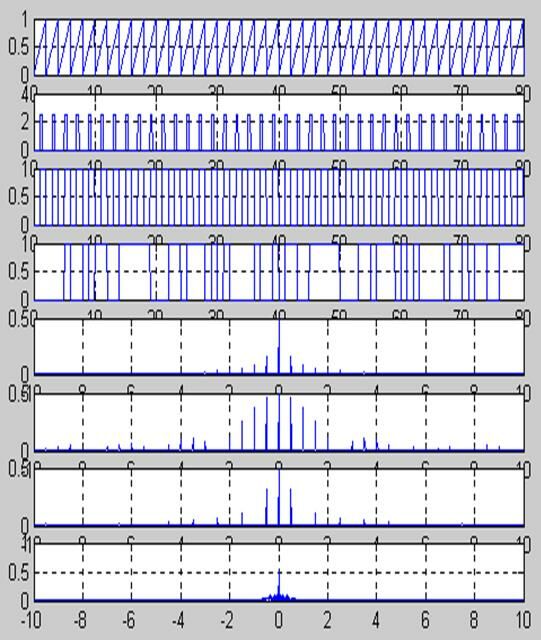
Примеры двусторонних спектров амплитуд периодических последовательностей импульсов и псевдослучайной последовательности

Период Т=2с, длительность τ элементарного символа ПСП -1с
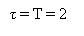
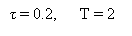
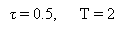
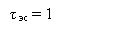