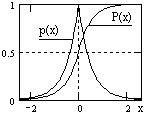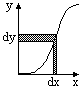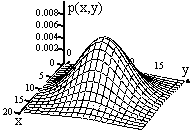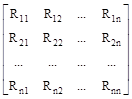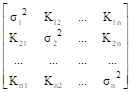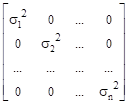Основы теории вероятностей случайных сигналов

Тема 8:   основы  теории  вероятностей случайных сигналов

Таковы первичные законы, установленные природой.

Вергилий. Георгики. (Римский  поэт)

"Природа не злонамеренна, но коварна". Это не закон. Это только следствие теории вероятностей. И все же непонятно, почему единственная муха в ресторане падает именно в мой суп.

Владимир Бакаев. Наблюдения. (Уральский геофизик)

Содержание:  8.1. Основные понятия теории вероятностей. События и явления. Классификация случайных событий. Сумма событий. Произведение событий. Полная группа событий. Сложные события. 8.2. Вероятности случайных событий. Частотное определение. Определение на основе меры. Основные положения теории вероятностей. Сложение вероятностей. Условная вероятность. Умножение вероятностей. Независимость событий. Формула полной вероятности. Формула Байеса. 8.3. Случайные величины. Общие понятия. Вероятности случайных величин. Функции от случайной величины. Моменты распределения. Основные числовые характеристики случайных величин. Некоторые распределения случайных величин. Характеристическая функция.  8.4. Системы случайных величин. Функция распределения вероятностей системы. Плотность вероятностей системы. Условные законы распределения. Функции регрессии. Статистическая независимость случайных величин. Моменты систем случайных величин. Сумма и разность случайных величин. Литература.

8.1. Основные понятия теории вероятностей [л28,л29].

            Теория вероятностей - один из разделов математики, в котором изучаются закономерности случайных массовых событий, явлений и процессов независимо от их физической природы.

            События и явления. Все события и явления реального мира разделяются на закономерные (детерминированные) и случайные (вероятностные).

Рекомендуемые материалы

            Закономерные события происходят при создании определенных условий, подчиняются определенным физическим законам и на основании этих законов однозначно предсказываются и изменяются. Возникновение тока в электрической цепи при подключении ее к источнику напряжения - закономерное событие, а сила тока в цепи может определяться и изменяться на основании закона Ома. Закономерное явление - это система, совокупность или последовательность закономерных событий. Генерация импульсного потока - закономерное явление, т.к. и форма импульсов, и время их появления задаются определенными физическими процессами в электрической схеме генератора.

            Случайным событием называется такое событие, изменить или предсказать которое в процессе случайного явления невозможно. Случайное событие - это результат (исход) конкретной единичной реализации случайного явления. Так, выпадение чисел 1-6 при бросании игральной кости - случайное явление. Выпадение числа 6 в единичном испытании - случайное событие. Если оно может задаваться, то это уже не игральная кость, а инструмент шулера. Типовое обозначение случайных событий - крупными буквами алфавита (например, событие А - выпадение 1 при бросании кости, событие В - выпадение 2 и т.д.).

            Случайность событий может быть обусловлена как собственной физической природой явлений, что характерно для большинства физических процессов в микромире (например, распад радиоактивных ядер), так и определенным вероятностным характером реализации явлений в силу их многофакторной и, как правило, нелинейной зависимости от внешних и внутренних условий, что характерно для процессов в макромире. Например, индивидуализация исхода  бросания игральной кости начинается с вариации некоторых начальных условий (положение в пространстве, скорость и направление движения, момент инерции, момент вращения и пр.) и продолжается на всем пути движения кости вплоть до остановки (трение о воздух, положение в момент удара о стол, поглощение энергии удара и пр.). Невозможность точного повторения всех условий опыта определяет случайность результата.

Нетрудно заметить, что понятие случайности явлений, а равно и границы между случайными и закономерными явлениями, довольно расплывчато и существенно зависит не только от природы самих явлений, но и от возможностей задания постоянных условий реализации явлений и фиксирования результатов. Падение напряжения на резисторе при задании через него тока - явление закономерное и значение напряжения может быть "предсказано" со сколь угодно высокой точностью при соответствующей точности задания сопротивления резистора и значения тока. Однако, как известно, если провести серию измерений этого напряжения прибором более высокой точности, то результаты измерений следует отнести к величинам случайным. Измеренные значения не будут выходить за пределы заданной точности, но и не будут повторяться в силу влияния самых различных дестабилизирующих факторов (температура, влажность, электромагнитные помехи и т.п.) как на сам измерительный прибор, так и на объект измерений. Более того, даже если мысленно идеализировать условия опыта и повысить точность задания параметров объекта, то и в этом случае мы выйдем на определенную случайность результатов измерений уже в силу дискретной природы самого электрического тока и флюктуаций движения электронов в резисторе.

С практической точки зрения явление или процесс считаются случайными, если в их формировании в той или иной форме присутствует неопределенность и невозможно с заданной  точностью предсказать результаты их конкретных реализаций, физического отображения и измерения в ходе контролируемых экспериментов или повторить в ходе многократных реализаций.

            Классификация случайных событий. Событие называют достоверным (и обозначают индексом W), если оно однозначно и предсказуемо. Выпадение суммы чисел больше 1 и меньше 13 при бросании двух костей - достоверное событие. Событие является невозможным (и обозначается индексом Æ), если в данном явлении оно полностью исключено. Сумма чисел, равная 1 или большая 12 при бросании двух костей - события невозможные. События равновозможны, если шансы на их появление равны. Появление чисел 1-6 для игральной кости равновозможно.

            Два события называются совместными, если появление одного из них не влияет и не исключает появление другого. Совместные события могут реализоваться одновременно, как, например, появление какого-либо числа на одной кости ни коим образом не влияет на появление чисел на другой кости. События несовместны, если в одном явлении или при одном испытании они не могут реализоваться одновременно и появление одного из них исключает появление другого (попадание в цель и промах несовместны).

            Сумма событий представляет собой такое объединение событий в одно новое событие, сущность которого заключается в реализации хотя бы одного из объединяемых событий:  S = A+B+...+N.  Такая операция представляет собой аналог дизъюнкции - логического сложения (логическое "ИЛИ"), и может записываться в виде S = AÈBÈ...ÈN. Так, если события А,В,С - поражение цели соответственно при 1-ом, 2-ом и 3-ем выстреле, то событие S=A+B+C - поражение цели вообще, т.е. любым выстрелом, в том числе двукратное и трехкратное. 

            Произведение событий представляет собой совмещение событий в одном новом событии, в совместном появлении всех совмещаемых событий:  S = A×B× ... ×N.  Такая операция представляет собой аналог логической конъюнкции (логическое "И"), и может записываться в виде S = AÇBÇ...ÇN. Продолжая предыдущий пример, событие Z - трехкратное попадание в цель, определяется выражением: Z = A×B×C.

            Попутно заметим, что для логических операций имеем: А+А=А и А×А=А. 

            Полная группа событий. События какого-либо случайного явления образуют полную группу, если в результате единичной реализации явления обязательно произойдет хотя бы одно из них, т.е. выполняется условие: А+В+ ... +N = W (сумма событий полной группы º достоверное событие). Выпадение чисел 1-6 при бросании кости - полная группа событий.

            Если полную группу образуют только два несовместных события, как выпадение герба или решки при бросании монеты, то такие события называются противоположными. При обозначении одного из таких событий определенным индексом, например - А, второе обычно обозначается тем же индексом с крышкой сверху: . Соответственно А+= W. Произведение несовместных событий является событием невозможным. В частности,  А×= Æ.

            Сложные события. Различают элементарные (простые) и сложные события. Элементарные события не разделяются на составные события. Выпадение числа при бросании кости - элементарное событие. Сложные события составляются из двух или нескольких элементарных событий. Так, если в примере с тремя выстрелами в цель нас интересует событие D, заключающееся в попадании в цель не менее двух раз, то оно определяется следующим выражением:

D = A×B×+A××C+×B×C+A×B×C

8.2. Вероятности случайных событий [л30,л28,л29].

Предсказание конкретной реализации случайных событий невозможно. Однако интуитивная ориентировка в случайных событиях известна каждому. Если при игре в кости дважды выпали две шестерки, то едва ли кто-нибудь в третий раз поставит на 12 очков.  Это определяется тем, что и случайные события подчиняются определенным вероятностным закономерностям и при повторениях испытаний предсказуемы "в среднем".

Понятие вероятности событий относится к фундаментальным понятиям теории вероятностей. Вероятность случайного события является количественной мерой степени объективной возможности появления этого события в единичном опыте (в единичной реализации случайного явления). На протяжении последних трех веков достаточно интенсивного развития теории вероятностей многие ученые делали попытки сформулировать это фундаментальное понятие на основе строгой логики. Приведем только два из них.

            Частотное определение. При N реализациях некоторого случайного явления случайное событие А наблюдалось n раз. Если случайные события в этом явлении взаимно независимы, несовместны и составляют полную группу, то вероятность события А определяется выражением:

                                                                       P(A) =                                             (8.2.1)

            Так как диапазон значений n в данном выражении ограничен интервалом 0 £ n £ N, то отсюда следует, что значения вероятностей событий заключены в интервале от 0 до 1.

Пример.  В урне находятся 5 белых и 7 черных шаров. Какова вероятность извлечь из урны 3 белых шара?

Общее число возможных способов извлечь 3 шара из 12 равно числу сочетаний из 12 по 3:

N = 12!/(3!×9!) = 220.

Число возможных сочетаний из 5 белых шаров по 3:    n = 5!/(3!×2!) = 10.

Искомая вероятность:   P = n/N = 10/220.

            При практических оценках вероятностей значение (n/N) называют относительной частотой (или частностью) данного события в данной серии наблюдений. Относительная частота событий при многократных наблюдениях является достаточно устойчивой величиной, флюктуирующей в окрестностях вероятности данных событий, причем величина флюктуаций тем меньше, чем больше количество наблюдений.

            Определение на основе меры. Введем пространство (множество) W, элементы которого w_i являются случайными элементарными событиями, т.е. W =w_i. Определим в этом пространстве неотрицательную меру P(w), которую назовем вероятностью, со следующими свойствами:

            1. P(W) = 1, т.е. вероятность появления события, принадлежащего к данному пространству (w_i Î W), равна 1 (условие нормировки меры).

            2. Если подмножества элементарных событий А Î W и В Î W, каждое из которых принадлежит данному пространству W, не имеют общих элементов, то Р(А+В) = Р(А) + Р(В), т.е. вероятность того, что наблюдаемое событие принадлежит либо подмножеству А, либо подмножеству В,  равна сумме вероятностей наблюдать это событие отдельно в подмножествах А и В.

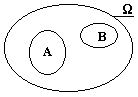
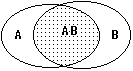
            Для иллюстрации различных положений теории вероятностей удобно использовать условные графические отображения пространств случайных событий, пример которых приведен на рис. 8.2.1. Полное пространство W элементарных событий w_i ограничивается произвольным контуром, площадь которого принимается равной 1 и равна вероятности появления событий w_i в пространстве W, при этом полагается, что события w_i равномерно заполняют пространство W. Группы событий w Î A или w Î В отображаются соответственно замкнутыми контурами внутри пространства W с площадями, равными вероятностям событий А и В.

            Основные положения теории вероятностей вытекают непосредственно из определения понятия вероятности.

            1. Вероятность любого случайного события А является неотрицательной величиной, значение которой заключено в интервале от 0 до 1.

0 £ Р(А) £ 1.

            2. Вероятность достоверного события равна 1.

                                                                       Р(W) = 1.                                                    (8.2.2)

            В общем случае событие W представляет собой сумму полной группы возможных элементарных событий данного случайного явления: W =w_i. Следовательно,  вероятность реализации хотя бы одного случайного события из полной группы возможных событий также равна 1, т.е. является событием достоверным.

            Сумма противоположных событий тоже составляет полную группу событий и соответственно вероятность суммы противоположных событий равна 1 (рис. 8.2.2):

                                                 P(A+) = 1.                                       (8.2.3)

            Примером может служить бросание горсти монет. Орел или решка для каждой монеты – противоположные события. Сумма событий для горсти в целом равна 1 независимо от соотношения выпавших орлов и решек.

            3. Вероятность невозможного события равна 0.

                                                           Р(Æ) = 0.                                                              (8.2.4)

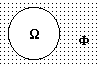
            Пусть Ф - пустое пространство (не содержащее событий). Тогда W+Ф = W и пространство W не содержит событий, общих с пространством Ф (рис. 8.2.3). Отсюда следует, что Р(W+Ф) = Р(W) + Р(Ф) = Р(W), что выполняется при Р(Ф) = 0. Другими словами, если одно из событий обязательно должно происходить, то вероятность отсутствия событий должна быть равна нулю. Но при этом W является достоверным событием, а Ф = Æ (невозможное событие) и соответственно Р(Æ) = 0.

            Сложение вероятностей зависит от совместности и несовместности событий.

            Несовместные события. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий. Это вытекает из того, что множество С = А+В включает подмножества А и В, не имеющие общих точек, и Р(А+В) = Р(А)+Р(В) по определению вероятности на основе меры. По частотному определению вероятности в силу несовместности событий имеем:

P(A+B) =  = += P(A) + P(B),

где n и m - число случаев появления событий А и В соответственно при N испытаниях.

            Противоположные события также являются несовместными и образуют полную группу. Отсюда, с учетом (8.2.3):

                                                            P() = 1 - Р(А).                                                  (8.2.5)

            В общем случае для группы несовместных событий (рис. 8.2.4):

                        P(A+B+...+N) = P(A) + P(B) + ... + P(N),                   (8.2.6)

если все подмножества принадлежат одному множеству событий и не имеют общих точек (попарно несовместны). А если эти подмножества образуют полную группу событий, то с учетом (8.2.2):

                                 P(A) + P(B) + ... + P(N) = 1.                              (8.2.7)

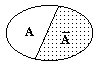
            Совместные события. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления (рис. 8.2.5):

                             P(A+B) = P(A) + P(B) - P(A×B).                      (8.2.8)

            Разобьем события А и В каждое на два множества, не имеющие общих точек: А', A'' и B', B''. Во множества А'' и B'' выделим события, появляющиеся одновременно, и объединим эти множества в одно множество С. Для этих множеств действительны выражения:

С = A''×B'' º А'' º В'' º А×В,     P(C) = P(A'') = P(B'') = P(A×B).

P(A) = P(A')+P(A''),        P(A') = P(A)-P(A'') = P(A)-P(A×B).

P(B) = P(B')+P(B''),        P(B') = P(B)-P(B'') = P(B)-P(A×B).

            Множества A', B' и С не имеют общих точек и можно записать:

P(A+B) = P(A'+B'+C) = P(A') + P(B') + P(С).

            Подставляя в правую часть этого уравнения вышеприведенные выражения, приходим к выражению (8.2.8). Физическая сущность выражения достаточно очевидна: суммируются вероятности событий А и В и вычитаются вероятности совпадающих событий, которые при суммировании сосчитаны дважды.

Пример.  Вытащим одну карту из колоды (52 карты). Какова вероятность того, что карта окажется или тузом, или пиковой мастью?

Р = Р(туз) + Р(пики) - Р(туз пик) = (4/52) + (13/52) - (1/52) = 16/52.  

            В общем случае, для m различных событий А₁, А₂, ..., А_m:

    P(A₁+...+ A_m) =P(A_i) -P(A_i×A_j) +P(A_i×A_j×A_k) -...+(-1)^m+1P(A₁×A₂× ... ×A_m).    (8.2.9)

            На рис. 8.2.6 на примере трех пространств можно видеть причины появления в выражении (8.2.9) дополнительных сумм вероятностей совпадающих пространств и их знакопеременности. При суммировании вероятностей пространств А,В и С, имеющих общее пространство АВС, его вероятность суммируется трижды, а при вычитании вероятностей перекрывающихся подпространств АВ, АС и ВС трижды вычитается (т.е. обнуляется), и восстанавливается дополнительным суммированием с вероятностью пространства АВС.

            Условная вероятность совместных событий. Предположим, что в пространстве событий с полным числом исходов N событие А может осуществляться n₁ способами (вероятность P(A) = n₁/N), событие В - n₂ способами, а события А и В одновременно - n₁₂ способами. При этом:

                                   P(AВ) = n₁₂/N = (n₁/N)(n₁₂/n₁) = P(A)×(n₁₂/n₁).                            (8.2.10)

            Второй сомножитель выражения (8.2.10) из общего числа случаев n₁ события А определяет долю, когда одновременно происходит и событие В, т.е. вероятность события В при условии, что произошло событие А. Эта вероятность называется условной вероятностью события В по событию А и записывается в виде Р(В/А):

                                                  Р(В/А) = Р(АВ)/Р(А).                                                  (8.2.11)

Пример.  Вытащим две карты из колоды (52 карты). Событие А - первая карта определенной масти. Событие В - вторая карта той же масти. Какова вероятность появления второй карты той же масти?

Р(А) = 13/52.  Карта не возвращается в колоду, следовательно, Р(В/А) = (13-1)/(52-1). 

            В общем случае может определяться условная вероятность события В в предположении, что произошли события А₁, А₂ и др.: Р(В/А₁,А₂,...).

            Для условной вероятности событий B по событиям A применяется также обозначение Р_A(B).

            Умножение вероятностей совместных событий. Формула определения вероятности события А×В (А и В одновременно, рис. 8.2.7), которую обычно называют формулой умножения вероятностей, непосредственно следует из выражения (8.2.11):

                        Р(АВ) = Р(А)×Р(В/А) º Р(В)×Р(А/В).                 (8.2.12)

Пример.  Вытащим две карты из колоды (52 карты). Событие А - первая карта определенной масти. Событие В - вторая карта той же масти. Какова вероятность появления двух карт одной масти?

Р(А) = 13/52.  Р(В/А) = (13-1)/(52-1).  Р(АВ) = (13×12)/(52×51) @ 0.0588

            В общем случае, вероятность умножения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других:

                        P(A₁×A₂×...×A_n) = P(A₁)×P(A₂/A₁)×P(A₃/A₂A₁)× ... ×P(A_n/A_i).                (8.2.12')

            Независимость событий. Если появление событий А не изменяет вероятности появления событий В, равно как и появление событий В не изменяет вероятности событий А, то события А и В считаются независимыми. Для таких событий Р(А/В) = Р(А), Р(В/А) = Р(В) и Р(А×В) = Р(А)×Р(В).

Пример.  Вытащим одну карту из колоды (52 карты). Пусть событие А - появление туза, событие В -появление пиковой масти.

Р(А) = 4/52.  Р(В) = 13/52.  Р(АВ) = 1/52.  Р(АВ) = Р(А)Р(В) = (4/52)(13/52) = 1/52.

События А и В независимы.

            В общем случае, группы событий А, В, ... N считаются независимыми в совокупности в том и только в том случае, если выполняется равенство:

                                   P(A×B× ... ×N) = P(A)×P(B)× ... ×P(N).                                            (8.2.13)

            Подмножества, образованные из независимых событий, также являются независимыми. Если условие (8.2.13) не выполняется, но выполняется для каждой пары событий из этой группы (А×В, А×С, В×С и пр.), то такие события называются попарно независимыми.

            Формула полной вероятности. Систему событий А₁, А₂, ...,A_N называют конечным разбиением (или просто разбиением), если они попарно несовместны, а их сумма образует полное пространство событий:

                                                           А₁ + А₂ + ... + А_N = W.                                         (2.2.14)

            Если события А_i образуют разбиение пространства событий и все P(A_i) > 0, то для любого события В имеет место формула полной вероятности:

                                                           P(B) =P(A_k)×P(B/A_k),                                     (8.2.15)

что непосредственно следует из (8.2.14) для попарно несовместных событий:

B = B×W = BA₁+BA₂+...BA_N.

P(B) = P(BA₁)+P(BA₂)+... +P(BA_N) = P(A₁)P(B/A₁)+P(A₂)P(B/A₂)+...+P(A_N)P(B/A_N).

Пример.  B урне находится N шаров, М белых и N-M черных. Событие А - первый вынутый шар белый, который в урну не возвращается. Какова вероятность события В, что второй вынутый шар будет белым?

Р(А) = M/N.  Р() = (N-M)/N.  Р(В/A) = (M-1)/(N-1).  Р(В/) = M/(N-1).

Отсюда:  Р(В) = Р(А)Р(В/А) + Р()Р(В/) = M/N, т.е. Р(В) = Р(А). Аналогично можно вычислить вероятность события С, что третий вынутый шар будет белым, и так далее, причем все вероятности вынуть белый шар на любой попытке равны M/N.

Этот результат давно известен и применяется, например, при жеребьевке, определяя независимость результатов жеребьевки от порядка ее участников при вынимании шаров.

            Формула Байеса (или формула гипотез). Если для пространства событий A_i выполнено условие (8.2.14) и для произвольного события В имеет место формула полной вероятности (8.2.15), то одновременно для любой комбинации событий В и А_k имеет место и формула умножения вероятностей (8.2.12)

Р(А_kВ) = Р(А_k)×Р(В/А_k) º Р(В)×Р(А_k/В),

из которой следует:

Р(А_k/В) = Р(А_k)×Р(В/А_k) / Р(В).

            Заменяя в этом уравнении выражение Р(В) формулой полной вероятности (8.2.15), получаем формулу Байеса:

                                          Р(А_k/В) = Р(А_k)×Р(В/А_k) /P(A_k)×P(B/A_k).                      (8.2.16)

            Нетрудно видеть, что знаменатель функции является нормировочным коэффициентом приведения суммы вероятностей к 1:

Р(А_k/В) = Р(А_k)×Р(В/А_k) /P(A_k)×P(B/A_k) = 1

            Смысл формулы Байеса заключается в следующем. Пусть A_k - возможные состояния (гипотезы) события А, для которых предполагается определенная плотность распределения вероятностей P(A_k). Событие В - результат некоторого единичного измерения (опыта), при этом известны условные вероятности P(B/A_k) реализации событий В по гипотезам A_k. Формула Байеса позволяет уточнить значения вероятностей реализации событий A_k по результатам испытания с реализацией события В. Другими словами, если P(A_k) - априорная плотность распределения вероятностей событий A_k, то P(A_k/B) - апостериорная плотность распределения вероятностей событий A_k, уточненная по результатам опыта, исходом которого явилось событие В.

Пример. В одном районе "дикого" туризма прогнозирование количества А несчастных случаев на следующие сутки проводилось по следующей методике (для наглядности рассмотрим пример на конкретных условных данных).

Априорные вероятности P(А_k) несчастных случаев на текущий день, вычисленные по предыдущему дню:   P(А₁=0) = 0.2,  P(А₂=1) = 0.4,  P(А₃=2) = 0.3,  P(А₄=3) = 0.1.

За текущий день зарегистрировано 0 несчастных случаев (В = 0).

Условные вероятности P(B/A_k) вычислялись по формуле плотности распределения вероятностей редких событий (формула Пуассона):  P(B/A_k) = (A_k)^B×exp(-A_k) /B!

P(0/0) = 1,  P(0/1) = 0.368,  P(0/2) = 0.135,  P(0/3) = 0.05.

Нормировочный делитель формулы Байеса: P(A_k)×P(B/A_k) = 0.393.

Апостериорные вероятности P'(A_k) = P(A_k/B) = P(A_k/0) несчастных событий на следующий день:

P'(А₁=0) = 0.509,  P'(А₂=1) = 0.375,  P'(А₃=2) = 0.103,  P'(А₄=3) = 0.013.

Проверка: P'(A_k) = 1.

8.3. Случайные  величины  [л30,л31,л2,л4,л15].

Общие понятия. Под случайной величиной в узком смысле данного термина можно понимать числовое отображение исхода случайного явления или опыта, если в основе его формирования лежат определенные физические процессы, вероятностные по свое природе. Так, например, число гамма-квантов, зарегистрированных радиометром за произвольный временной интервал от радиоактивной пробы, является случайной величиной как в силу вероятностной природы самого радиоактивного распада, так и в силу вероятностного характера их распространения, рассеяния и поглощения в окружающей среде и в детекторе радиометра.

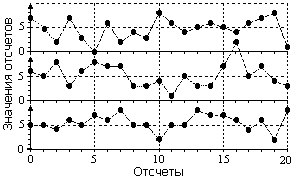
С общих позиций под случайной величиной и, соответственно, случайным сигналом ее отображения, понимают результаты фиксации такого явления (процесса), которые являются либо полностью непредсказуемыми, либо предсказуемы только "в среднем", с определенной средней квадратической погрешностью. Конкретный результат, зарегистрированный в определенном опыте, называют реализацией случайного явления. Отдельную реализацию случайного явления нельзя описать явной математической формулой, равно как и предсказать значения этой реализации в какие-либо моменты ее координатного распределения, т.к. она является одной из множества возможных. Множество реализаций, зарегистрированных в одних и тех же условиях для одного и того же объекта, называют ансамблем реализаций (или выборкой из генеральной совокупности - полного множества всех возможных значений). В качестве примера на рис. 8.3.1 приведено 3 реализации отсчетов радиометра, которые проводились в постоянных условиях по 20-ти секундным интервалам с односекундной экспозицией. Ансамбль реализаций позволяет характеризовать случайное явление определенными и достаточно устойчивыми статистическими данными.

Еще раз отметим, что отнесение тех или иных величин и отображающих их сигналов к случайным или неслучайным (детерминированным) в той или иной мере всегда относительно, особенно в геофизической практике. С одной стороны, ни в одной сколь угодно точно известной геологической обстановке нельзя исключить появления объекта или проявления какого-либо процесса, которые совершенно непредсказуемым образом могут повлиять на распределение информационного сигнала. С другой стороны можно отрицать и истинную случайность физических явлений и процессов, поскольку по мере накопления информации появляется возможность их описания все более точными математическими формулами детерминированного действия.

Множество возможных значений случайной величины принято называть пространством (множеством) состояний (генеральной совокупностью). Если пространство состояний образует континуум, то случайная величина является непрерывной. Если изменение состояний допускается для конечного (счетного) числа координат, то говорят о случайной непрерывной последовательности.

Случайную величину с конечным множеством состояний по непрерывной шкале координат называют дискретной, если она дискретна по множеству своих возможных значений. Если для случайного явления изменение состояний возможно только в конечном числе координат, то говорят о случайной дискретной последовательности. Для случайных явлений с дискретным множеством состояний статистические зависимости могут распространяться на ограниченное число k следующих друг за другом значений. Такие процессы называются марковскими k-го порядка.

Вероятности случайных величин. Исчерпывающим описанием случайных величин является плотность распределения вероятностей p(x) (кратко - плотность вероятностей) которая определяет вероятность реализации некоторого значения X_i в элементарном интервале значений dx:

p(x)dx = P(x < X_i £  x+dx).                                   (8.3.1)

            Основные свойства плотности вероятностей:

            1. p(x) ³ 0,  - ¥ < x <  ¥. Плотность вероятностей не отрицательна.

            2. p(x) dx = 1. Сумма вероятностей всех возможных значений случайной величины по данному пространству состояний должна быть равна 1, т.е. реализация одного из состояний должна быть достоверным событием.

            3. 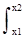p(x) dx = P(x₁<X£x₂). Интеграл от плотности вероятностей по определенному интервалу равен вероятности реализации случайной величины в этом интервале значений.

4. Функция P(x) = p(u) du определяет вероятность того, что значения случайной величины меньше или равны значению х.

Функция P(x) носит название функции распределения вероятностей (кратко - распределение вероятностей). Соответственно, производная от функции распределения вероятностей есть плотность вероятностей. Основные свойства функции распределения вероятностей:

1. Интервал определения функции: 0 £ P(x) £ 1,  - ¥ < x < ¥.

2. P(-¥) = 0, P(¥) = 1.

3. P(x) не уменьшается при возрастании х.

4. P(x₁<X £ x₂) = P(x₂) - P(x₁). 

На рис. 8.3.2 приведен пример функции плотности вероятностей p(x) = (a/2)exp(-a|x|)  и соответствующей функции вероятностей P(x).

Аналогичным описанием для случайных дискретных величин является непосредственно дискретное распределение вероятностей их значений:

P_i(x) = P(x_i < X_i £ x_i+1),         P(x_i) = 1.

            Функции от случайной величины. Допустим, что случайная величина Y связана со случайной величиной Х однозначной зависимостью y = f(x) (рис. 8.3.3). Интервалам dx соответствуют интервалы |dy| = |f'(x)|dx, при этом вероятности случайных величин в этих интервалах должны быть равны: p_x(x)dx = p_y(y)|dy|. Отсюда следует:

    p_y(y) = p_x(x)|dx/dy|,                             (8.3.2)

где аргумент х в правой части выражения должен быть выражен через x = g(y) - функцию, обратную y = f(x). Выполняя последнее, получаем:

p_y(y) = p_x[g(y)]|dg(y)/dy|,                                                  (8.3.2')

            Значения |dy| и последующие значения |dx/dy| и |dg(у)/dy| принимаются по модулю для исключения отрицательных значений в функции p_y(y), которых не может быть по определению и физической сущности плотности распределения вероятностей.

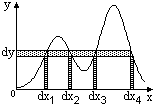
Если связь между значениями Х и Y неоднозначна, как, например, на рис. 8.3.4, и значению у может соответствовать несколько значений х, то вероятность попадания случайной величины у в интервал dy будет складываться из суммы вероятностей несовместных событий p_x(x₁)dx₁ + p_x(x₂)dx₂ + ..., откуда следует:

p_y(y) = p_i(x_i)|dx_i/dy| = p_x[g_i(y)]|dg_i/dy|,              (8.3.2'')

Пример. Связь случайных величин Х и Y задана выражением Y = aX+b. Плотность вероятностей величины Х соответствует распределению Гаусса: . Из уравнения связи величин Y и X имеем  x = (y-b)/a  и  |dx/dy| = 1/|a|, и соответственно получаем:

,     = b+a,    s_у² = а² s_х²

Моменты распределения. При решении многих практических задач нет особой необходимости в полной вероятностной характеристике каких-либо случайных величин, которую дает функция плотности распределения вероятностей. Очень часто приходится также иметь дело с анализом случайных величин, плотности вероятностей которых не отображаются аналитическими функциями либо вообще неизвестны. В этих случаях достаточно общее представление о характере и основных особенностях распределения случайных величин можно получить на основании усредненных числовых характеристик распределений.

Числовыми характеристиками случайных величин, которые однозначно определяются функциями распределения их вероятностей, являются моменты.

Начальные моменты n-го порядка случайной величины X (или просто моменты) представляют собой усредненные значения n-й степени случайной переменной:

    m_n º М{Xⁿ}º =  xⁿ p(x) dx,                             (8.3.3)

где M{Xⁿ} и - символические обозначения математического ожидания и усреднения величины Хⁿ, которые вычисляются по пространству состояний случайной величины Х.

Соответственно, для случайных дискретных величин:

m_n º М{Xⁿ}º =x_iⁿ p_i.                                  (8.3.3')

Центральные моменты n-го порядка, это моменты относительно центров распределения (средних значений) случайных величин:

m_n º M{(X-)ⁿ}º =(x-m₁)ⁿ p(x) dx,                   (8.3.4)

    m_n º M{(X-)ⁿ}º =(x_i-m₁)ⁿ p_i,                          (8.3.4')

где  - начальный момент 1-го порядка (среднее значение величины Х), X₀ = X- - центрированные значения величины Х.

Связь между центральными и начальными моментами достаточно проста:

m₁=0,    m₂=m₂-m₁²,    m₃=m₃-3m₂m₁+2m₁³,    m₄=m₄-4m₁m₃+6m₁²m₂-3m₁⁴,  и т.д.

Соответственно, для случайных величин с нулевыми средними значениями начальные моменты равны центральным моментам.

По результатам реализации случайных величин может производиться только оценка моментов, т.к. количество измерений всегда конечно и не может с абсолютной точностью отражать все пространство состояний случайных величин. Результаты измерений - выборка из всех возможных значений случайной величины (генеральной совокупности). Оценка моментов, т.е. определение средних значений n-й степени по выборке из N зарегистрированных значений, производится по формулам:

      = (1/N)x_iⁿ » ,       = (1/N)(x_i-)ⁿ » .          (8.3.5)

Погрешность оценок стремится к нулю при выборке N Þ ¥.

Основные числовые характеристики случайных величин - это начальный момент 1-го порядка (средние значение распределения случайных величин) и центральный момент 2-го порядка (дисперсия распределения).

Среднее значение распределения является характеристикой сдвига значений случайных величин относительно x = 0 и представляет собой значение центра рассеяния случайных величин, т.е.  математическое ожидание случайной величины по пространству возможных состояний:

M{X}º=x p(x) dx,       =x_n P(x_n).             (8.3.6)

            Если пространство возможных состояний случайных величин ограничено определенными конечными пределами, то соответственно интегрирование (или суммирование) осуществляется в этих пределах. В функциях от случайных величин постоянный множитель можно выносить за знак математического ожидания:

M{Y}= M{c×X} = c×M{X}.

            Оценка среднего значения по результатам N-выборки (выборочное среднее):

        = (1/N)x_i                                                (8.3.7)

            Значение  генеральной совокупности случайной величины Х является неслучайной величиной, в отличие от значения выборочного среднего , которое также является величиной случайной. Математическое ожидание величины  с использованием формулы (8.3.7):

M{} = (1/N) M{x_i} = (1/N) M{N×x_i} = M{X} = .

            Отсюда следует, что выборочное среднее есть несмещенная оценка среднего значения генеральной совокупности, т.е.   » .

Дисперсия распределения характеризует размер пространства состояний случайной величины, величину их рассеивания по значениям относительно среднего значения:

    D{X}º M{(X-)²}º M{X₀²}= (x-)² р(x) dx.                  (8.3.8)

Оценка дисперсии по результатам N-выборки производится по формулам:

D_x = (1/N)(x_i-)² » D{X}.                               (8.3.9)

     D_x º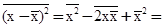- ².                          (8.3.9')

            Для функции с×Х, где с = const, имеем:

D{c×X}=M{(cX-M{cX})²}=M{(cX-cM{X})²}=M{c²(X-M{X})²}=c²×D{X}.

           

Среднее квадратическое отклонение случайной величины от математического ожидания (среднего значения), равное корню квадратному из значения дисперсии:

    s_х = ,                                             (8.3.10)

получило название стандарта (стандартного отклонения). Величину стандарта в относительных единицах среднего значения d_x = s/m_x называют вариацией или (в основном для временных процессов) флюктуацией значений случайной величины.

Пример.  Плотность распределения случайных величин Х:  p(x) = (a/2)exp(-a|x-b|), а=2, b=4.

Среднее значение и дисперсия: =x p(x) dx = b = 4,   D{X} =(x-b)² р(x) dx = 2/a² = 0.5.

       В опыте зарегистрированы:   Х = {2.75, 4.08, 3.9, 3.82, 3.68, 3.03, 4.16, 5.74, 3.78, 2.77, 4.03}.

 Среднее значение и дисперсия по выборке:

 = (1/11)x_i = 3.79,     = (1/11)x_i² = 15,     D_x = - ² = 0.62.

Погрешность оценок выборочных средних значений  в зависимости от N - размеров выборки вычисляется по дисперсии значений  (выражение (8.3.7)):

D() = D((1/N)x_i) = (1/N²) D(x_i) = (1/N) D(x_i),

т.е. дисперсия средних значений  по N-выборке в N раз меньше дисперсии самих значений случайных величин Х. Соответственно, точность оценки средних значений  определится выражением:

s() = s_x/.

            Точность оценки выборочного среднего значения случайных величин возрастает пропорционально корню квадратному из размеров выборки. По мере увеличения объема выборки выборочное среднее значение стремится к математическому ожиданию случайной величины как к своему пределу (закон больших чисел). В математической статистике доказывается также, что если случайная величина Х имеет среднее значение  и конечную дисперсию s_x², то при стремлении объема выборки N к бесконечности распределение выборочного среднего  будет стремиться к нормальному закону со средним значением  и дисперсией s_x²/N (центральная предельная теорема).

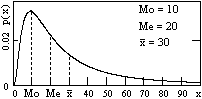
К числовым характеристикам случайных величин Х относятся также мода Мо_х, медиана Ме_х, асимметрия S_х и эксцесс Е_х.

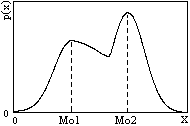
Мода распределения  - это наиболее вероятное значение случайных величин, которому соответствует максимум плотности вероятностей. Функции плотности вероятностей могут иметь больше одного максимума. Такие распределения называют много- или полимодальными. На рис. 8.3.5 приведен пример двумодального распределения.

Для одномодальных распределений,  симметричных относительно среднего значения, мода совпадает со средним значением, для асимметричных среднее значение обычно смещено относительно моды в сторону более длинного "хвоста" изменения плотности вероятностей.

Медиана распределения случайных величин Ме_х - это такое число (значение Х), относительно которого площади под функцией плотности вероятностей слева и справа равны друг другу, т.е.:

Р(X<Me_x) = Р(X>Me_x) = 0.5.

            Понятие медианы обычно используется для непрерывных случайных величин.

            В резко асимметричных распределениях случайных величин значения моды, медианы и среднего значения существенно расходятся, как, например, для логнормального распределения на рис. 8.3.6.     

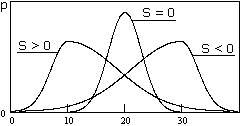
            Асимметрия (или скошенность) распределения случайных величин X - это безразмерное число, которое определяется выражением:

S_x = m₃/s_x³ º M{(X-)³/s_x³ º /s_x³.

            При Mo_x < Me_x асимметрия положительна (распределение вытянуто вправо, S > 0), при Mo_x > Me_x - отрицательна. Для симметричных распределений Mo_x = Me_x =и асимметрия равна нулю. На рис. 8.3.7 приведены плотности вероятностей случайных величин с разной асимметрией.

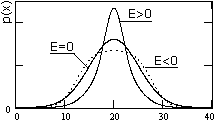
            Эксцесс (или крутость) распределения случайных величин также безразмерное число:

E_x = m₄/s_x⁴ - 3 º M{(X-)⁴/s_x⁴ -3 º /s_x⁴ - 3.

            Эксцесс характеризует форму функции плотности вероятностей по отношению к форме функции нормального распределения (см. ниже, выражение 8.3.15), значение эксцесса для которого равно 0. Если кривая распределения имеет более острую и высокую вершину при той же величине дисперсии, то значение эксцесса больше нуля, если более низкую и пологую - меньше нуля (рис. 8.3.8).

Оценка числовых характеристик функций от случайных величин может производиться непосредственно по числовым характеристикам случайных величин с использованием правила переноса ошибок.

Допустим, что случайная величина Y является функционально зависимой от случайной величины Х и определяется выражением  Y = g(x). Разложим это выражение в ряд Тейлора относительно математического ожидания :

       g(x) = g() + (x-)g'() + (x-)²g''()/2! + ...                 (8.3.11)

            Оценка математического ожидания :

M{g(x)}= M{g()}+M{(x-)g'()}+M{(x-)²g''()/2!}= g() + 0 + s_x²g''()/2! +...

            Отсюда, с точностью до членов второго порядка малости:

= g().                                                 (8.3.12)

            Оценка дисперсии распределения D(g(x)) = D_y:

    D_y = M{[g(x) - M{g(x)}]²} » M{[g(x)-g()]²}.                     (8.3.13)

            Из формулы (8.3.11) имеем:

g(x) - g() = (x-)g'() + (x-)²g''()/2! + ...

            С использованием этого выражения в (8.3.13) с ограничением до 2-го порядка:

D_y » M{[(x-)g'()]²} = [g'()]²×D_x.                            (8.3.14)

    s_y = g'()×s_x,      d_y = g'()×d_x.

         Для линейных функций g(x) ~ a×x+b выражения (8.3.12-14) являются точными.

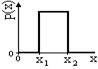
Некоторые распределения случайных величин.

Равномерное распределение. Случайная величина равновероятна в интервале значений от х₁ до х₂ (рис. 8.3.9):

                                                   р(х) = 1/(х₂-х₁),      х₁ £ х £ х₂,  

                                                           = 0,                 х < х₁, х > х₂.

                                               М{X}= (х₁+х₂)/2,    D{X}= (x₂-x₁)²/12.

            Для дискретной величины с N равноотстоящими друг от друга значениями:

P_i = 1/N,  M{X} = (x₁+x₂)/2,  D{X} = [(x₂-x₁)²/12][(N+1)/(N-1)].

            Распределение Гаусса (нормальное распределение). Плотность вероятностей нормального распределения случайных непрерывных величин Х задается двумя параметрами - среднего значения  (центра распределения) и дисперсии  s²:

.                              (8.3.15)

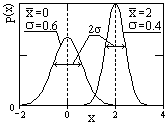
            Пример двух распределений Гаусса при разных средних значениях и дисперсиях приведен на рис. 8.3.10.

Плотность вероятностей случайной гауссовской величины имеет только один максимум, который соответствует x = , т.е. математическому ожиданию, при этом форма распределения симметрична относительно математического ожидания. При |х| Þ ¥  ветви кривой асимптотически приближаются к нулю. Изменение математического ожидания при s = const смещает максимум распределения вдоль оси х без изменения формы кривой. Ширина плотности вероятностей распределения пропорциональна стандартному отклонению s и на уровне 0.607 от максимального значения p(x)  равна 2s. Вероятность отклонений значений х от среднего значения  на величины, большие 3s, в нормальных распределениях равна 0.0028, что позволяет выполнять прямые и обратные прогнозные оценки:

x_max @ + 3s,    x_min @ - 3s,

@ (x_max+x_min)/2,   s @ (x_max-x_min)/6.

            Нормальное распределение играет большую роль в теории вероятностей и в математической статистике. Основная особенность его заключается в том, что оно является предельным законом, к которому при определенных условиях приближаются другие законы распределения. В частности, независимые случайные величины Х₁, Х₂, ..., Х_n, подчиненные каким угодно законам распределения (с весьма небольшими исключениями), при суммировании и других линейных комбинациях дают распределения, сколь угодно близкие к нормальному закону. Это позволяет нормальному распределению служить хорошей математической моделью для большинства многофакторных физических процессов. Линейные комбинации случайных гауссовских величин всегда являются гауссовскими.

            Распределение Пуассона является широко распространенным распределением случайных целочисленных дискретных величин. Оно задается только одним параметром l,  значение которого равно среднему значению случайных величин распределения и одновременно задает значение дисперсии распределения:

P_k = ,   k - целое.                                      (8.3.16)

= l,   D_k = l,   s_k =,   d_k = 1/.

Распределение Пуассона иногда называют распределением вероятностей количества редких событий, для оценки которых оно и применяется наиболее часто, безотносительно к их физической сущности. Условия справедливости распределения Пуассона применительно к каким-либо случайным явлениям (событиям) достаточно просты:

1. Случайная величина может принимать только нулевые и целые положительные значения (как, например, число отказов аппаратуры или телефонных звонков за определенный временной интервал, число треков от альфа-частиц на площади или в объеме трекового детектора и т.п.).

2. Вероятность отдельного события на бесконечно малом пространстве счета событий, на котором ведется их регистрация (время, площадь, объем и пр.)  пропорциональна величине этого пространства и при его стремлении к нулю также стремится к нулю, как бесконечно малая первого порядка, а вероятности событий более высокой кратности (2 и более событий) стремятся к нулю, как бесконечно малые более высоких порядков.

3. События в неперекрывающихся интервалах пространства счета событий статистически независимы.

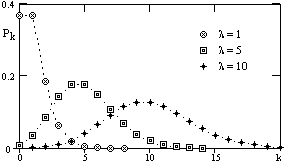
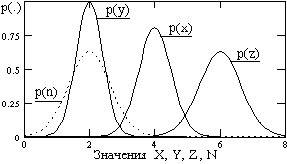
Пример.  Средняя скорость счета фоновых гамма-квантов детектором радиометра составляет m = 1 импульс в секунду.  Возможные экспозиции единичного измерения равны 1, 5 и 10 секунд. Все три условия справедливости закона Пуассона для процесса регистрации квантов выполнены. Значение l для распределения (8.3.16) будет определяться выражением  l = mT, где Т - экспозиция измерения. Расчетные значения вероятностей P_k для трех различных экспозиций приведены на рис. 8.3.11. Попутно заметим, что значение l для закона Пуассона не обязано быть целочисленным.

            Как видно на рис. 8.3.11, распределение Пуассона резко асимметрично при малых значениях l. По мере роста l распределение становится симметричным относительно = l и при l>20 может быть аппроксимировано однопараметровым распределением Гаусса с  = s² = l.

            Экспоненциальное распределение.  Этим законом отображается, например, распределение длительности интервалов между случайными событиями, соответствующими закону Пуассона, непосредственно из которого оно и может быть получено.

            Допустим, что для рассматриваемого явления значение l распределения Пуассона определяется выражением  l = nt, где n - среднее количество событий на единице интервала t (средняя скорость следования событий, если t - время). Длительность интервала между двумя последовательными событиями будет равна t+dt, если на интервале t не будет ни одного события (вероятность чего в соответствии с (8.3.16) равна Р₀ = (nt)⁰×e^-nt/0! = e^-nt), а на интервале dt Þ 0  произойдет одно событие (вероятность P₁ = (ndt)¹×e^-ndt/1! = ndt, так как e^-ndt Þ 1 при dt Þ 0). События в неперекрывающихся интервалах являются статистически независимыми, а, следовательно, искомая вероятность p(t)dt интервала t будет равна произведению вероятностей Р₀ и Р₁, т.е.  p(t)dt = e^-nt×ndt,  откуда получаем выражение для плотности распределения вероятностей случайной непрерывной величины t:

p(t) = n×e^-nt,   t ³ 0.                                               (8.3.17)

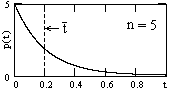
            Пример распределения при n = 5 приведен на рис. 8.3.12. Распределение, как и положено, является нормированным:

p(t) dt = 1.

            Среднее значение длительности интервала:

= t p(t) dt = nt e^-nt dt = 1/n.

            Среднее квадратическое значение:

= t² p(t) dt = nt² e^-nt dt = 2/n².

            Дисперсия, среднее квадратическое отклонение и относительные флюктуации:

D_t = -² = 1/n²,     s_t = = 1/n,     d_t = s_t/ = 1.

            Как видно на рис. 8.3.12, для распределения наиболее вероятны короткие интервалы, меньшие среднего значения интервалов. Соответственно, для выдерживания среднего значения = 1/n, большее количество коротких интервалов компенсируется меньшим количеством, но длинных интервалов, в 2-3 и более раз превышающих средний интервал, что приводит к большим флюктуациям длины интервалов (среднее квадратическое отклонение равно средней длине интервалов). При работе с пуассоновскими распределениями это следует учитывать, так как длительное отсутствие регистрации событий в процессе единичной реализации какого-либо случайного процесса может вовсе не свидетельствовать об отсутствии самого процесса.

            Характеристическая функция С(t) случайной величины Х с плотностью вероятностей р(х) определяется выражением:

C(v) =  p(x) exp(j2pvx) dx.                          (8.3.18)

            Нетрудно заметить, что это выражение совпадает с обратным преобразованием Фурье функции р(х). Отсюда следует:

p(x) =  C(v) exp(-j2pvx) dv,                         (8.3.19)

т.е. плотность вероятностей случайной величины может рассматриваться, как частотный спектр характеристической функции случайной величины, а последняя, в свою очередь, как координатное представление распределения случайной величины.

            Через определение (или вычисление) характеристической функции упрощается нахождение моментов случайной величины любого порядка, а именно:

dⁿC(v)/dvⁿ = jⁿxⁿ p(x) exp(j2pvx) dx.

            Принимая v = 0 и сравнивая результат с выражением (8.3.3), получаем:

m_n = j^-n dⁿC(0)/dvⁿ = j^-n C⁽ⁿ⁾(0).                           (8.3.20)

            С помощью характеристической функции и выражений (8.3.2) можно также находить плотность вероятностей случайных величин, подвергнутых функциональным преобразованиям.

8.4.  Системы случайных  величины  [л31,л2,л4,л15].

Свойства случайных сигналов принято описывать характеристиками совокупности случайных величин {Х₁,Х₂,...,X_n}, которую называют также системой или совместным распределением случайных величин. Система реализуются в процессе совместных измерений или в процессе последовательных измерений одной реализации. И в том, и в другом случае совместное распределение величин может рассматриваться как n-мерный случайный вектор Х. Теория систем случайных величин наиболее детально разработана для двух случайных величин, измеряемых по одной координате (времени, пространству и т.п.).

Пример 1.  Результат накопления информации в каналах многоканального спектрометра от датчика ионизирующего излучения представляет собой совокупность (систему) случайных величин X_i (i = 1,2,...,k - номер канала спектрометра), каждая из которых распределена по закону Пуассона. Результат единичной экспозиции измерений (единичной реализации системы) - совместное распределение отсчетов x_i. В совокупности эти отсчеты представляют собой k-мерный случайный вектор Х как реализацию случайного сигнала - определенного спектрального распределения излучения с математическим ожиданием отсчетов в каналах M{X_i}.

Пример 2. По стволу скважины с шагом дискретизации данных 10 см зарегистрирована цифровая диаграмма ГК - мощности экспозиционной дозы гамма-излучения пород. Последовательность цифровых отсчетов x_i диаграммы (i = 1,2,...k) в силу природы радиоактивного распада представляет собой одну реализацию случайных величин X_i (k-мерный случайный вектор Х).

Пример 3. Дополнительно к мощности экспозиционной дозы в примере 2 по стволу скважины зарегистрированы цифровые диаграммы гамма-гамма-каротажа (ГГК) y_i, нейтронного каротажа (НК) n_i и нейтронного гамма-каротажа (НГК) z_i. Эти диаграммы также могут рассматриваться как единичные реализации систем случайных величин соответственно Y_i, N_i и Z_i. Но одновременно однономерные совокупности случайных величин x_i, y_i, n_i и z_i (пространственные сечения) также могут рассматриваться в виде 4-х мерных систем случайных величин Xi, Yi, Ni и Zi, зарегистрированных последовательно по одной пространственной координате, равно как и в виде одной 5-ти мерной системы случайных величин X, Y, N, Z (5-ти мерный случайный вектор или 5-ти мерный случайный сигнал).

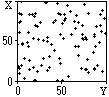
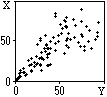
            При рассмотрении систем случайных величин, и особенно дву- и трехмерных, удобно использовать геометрическую интерпретацию систем. Так, например, пространство системы двух случайных величин (X,Y) можно представлять себе на плоскости x0y с координатами X и Y, где каждой паре (x_i,y_i) реализации случайных величин соответствует точка на плоскости. На рис. 8.4.1 приведен пример такого графического отображения реализаций системы независимых случайных величин (X,Y). Аналогично в трехмерном пространстве могут отображаться трехмерные системы случайных величин.

            Рассмотрение систем случайных величин будем проводить, в основном, на двумерных системах, основные положения которых легко распространяются и на многомерные системы.

            Функция распределения вероятностей системы (n-мерное совместное распределение вероятностей) определяет вероятность реализации системы событий Х, как появления событий {Х₁,Х₂,...,X_n} в одной реализации:

P(x₁,x₂, ... ,x_n) = P(X₁ £ x₁, X₂ £ x₂, ... ,X_n £ x_n).                            (8.4.1)

            Геометрически (рис. 8.4.2) функция распределения системы двух случайных величин (X,Y) представляет собой вероятность реализации случайных точек в левом нижнем бесконечном квадранте (заштриховано) с вершиной в точке (x,y).

            Свойства многомерной функции распределения в целом аналогичны одномерной функции и кратко могут быть описаны следующим образом:

            1. 0 £ P(x₁,x₂, ... ,x_n) £ 1, -¥ <x₁< ¥, -¥ <x₂< ¥ , ... , -¥ <x_n< ¥.

            2. P(x₁,x₂, ... ,x_n) есть монотонно неубывающая функция по всем x_i.

            3. P(x₁,x₂, ... ,x_n) = 0, если хотя бы один из аргументов равен - ¥.

            4. P(x₁,x₂, ... ,x_n) = 1, если все без исключения аргументы равны  ¥.

            5. P( ¥,x₂, ... ,x_n) = P₁(x₂, ... ,x_n), P(x₁,¥, ... ,x_n) = P₂(x₁,x₃, ... ,x_n), ... и т.д. для любых значений x_i = ¥ в любых комбинациях вплоть до P(¥,¥, ... ,x_n) = P_j(x_n), при этом функции P_i для разных комбинаций аргументов не обязаны иметь один и тот же вид. Геометрическое отображение данного свойства для двумерной системы (X,Y) приведено на рис. 8.4.3.

Плотность вероятностей системы удовлетворяет соотношению:

     p(x₁,x₂,...,x_n) dx₁ dx₂ ... dx_n = P{x₁<X₁£x₁+dx₁, ... ,x_n<X_n£x_n}.           (8.4.2)

  p(x₁,x₂,...,x_n) = P(x₁,x₂, ... ,x_n) /.                         (8.4.3)

            Плотность вероятностей двумерной системы можно изобразить геометрически в виде поверхности распределения вероятностей, пример которой приведен на рис. 8.4.4.

Свойства многомерной плотности распределения вероятностей вытекают из свойств функции распределения вероятностей и в целом аналогичны одномерной плотности вероятностей, а именно (на примере двумерной плотности вероятностей):

            1. p(x,у) ³ 0,  - ¥ < x < ¥, - ¥ < x < ¥. Плотность вероятностей не отрицательна.

            2. p(x,у) dx dy = 1. Сумма вероятностей всех возможных значений системы случайных величин (X,Y) по пространству состояний равна 1.

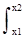
            3. p(x,y) dx dy = P(x₁<X£x₂, y₁<Y£y₂). Двойной интеграл от плотности вероятностей по определенным интервалам случайных величин Х и Y равен вероятности реализации системы случайных величин в этом интервале значений Х и Y.

По известной n-мерной плотности вероятностей может определяться m-мерная плотность при m<n интегрированием по "лишним" координатам:

p(x₁,x₂,...,x_m) = ... p(x₁,x₂,...,x_n) dx_m+1 ... dx_n.                  (8.4.4)

            Условные законы распределения. Выражение (8.4.4) при известном законе плотности распределения вероятностей системы случайных величин позволяет определить плотность вероятностей любой из случайных величин, входящих в систему. Обратная задача не может решаться столь просто, поскольку известные законы распределения отдельных случайных величин не определяют связей между величинами, если последние существуют. Для решения задачи требуется задание условных законов распределения, т.е. плотности распределения вероятностей одной случайной величины при определенных значениях других случайных величин.

            Случайные величины, входящие в систему, реализуются совместно. С учетом этого, условные законы распределения случайных величин можно получить переходом от условных вероятностей совместных событий (8.2.10-12) к плотности распределения вероятностей. В общем случае, условные законы распределения также могут быть многомерными, т.е. определять вероятность реализации одной из случайных величин при условии реализации определенных значений других величин системы. Однако на практике даже для многомерных систем используются, в основном, попарные двумерные зависимости. Так, для двумерных случайных систем условные плотности вероятностей величины X по значениям величины Y и величины Y по Х определяются выражениями:

     p(x/y) = p(x,y)/p(y),     p(y/x) = p(x,y)/p(x).                             (8.4.5)

            Отсюда, определение плотности вероятностей двумерной системы производится по формулам:

p(x,y) = p(x)×p(y/x) º p(y)×p(x/y).                                      (8.4.6)

            При известных многомерных законах распределений анализ попарных двумерных распределений производится с использованием выражения (8.4.4).

            Функции регрессии.  Из выражений (8.4.5-6) следует, что в системе зависимых случайных величин математические ожидания величин также являются зависимыми, т.е. функциями средних значений одной величины от значений другой величины:

        (y) = M{X/y}=x p(x/y) dx,    (x) = M{Y/x}=y p(y/x) dy.         (8.4.7)

            Уравнения

x = (y),     y=(x)                                                (8.4.8)

называются уравнениями регрессии соответственно X по Y и Y по Х. В общем случае уравнения регрессии для многомерных систем также могут быть многомерными, типа x = (y,z,...) и пр.

            Статистическая независимость случайных величин. Для совместной системы случайных величин X случайные величины системы (X₁, X₂, ...) статистически независимы друг от друга, если реализация одной из величин ни каким образом не определяет и не влияет на реализацию других величин. Так, например, при игре в кости реализация в одном бросании числа на одном кубике не влияет на появление каких-либо чисел на других кубиках. Если такая зависимость появляется, то это свидетельствует о мошенничестве.

Статистически независимы, как правило, случайные величины, связанные с источниками различной физической природы. В строго корректном понимании данного термина случайные события статистически независимы тогда и только тогда, когда выполняется условие:

p(x₁,x₂,...,x_n) = p₁(x₁) p₂(x₂) ... p_n(x_n).                               (8.4.9)

Пример.  Определить независимость случайных величин Х и Y в двумерной системе по заданной плотности распределения вероятностей системы.

1.  p(x,y) = 1/[p²(1+x²+y²+x²y²)].  Выражение 1+x²+y²+x²y² может быть разделено по переменным на множители (1+х²)(1+у²), а, следовательно, p(x,y) = p(x)×p(y). Случайные величины Х и Y независимы.

2.  p(x,y) = x+y, 0 £ x £ 1, 0 £ y £ 1.  Cоответствующие одномерные плотности вероятностей:

p(x) = 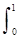 (x+y) dy = x+1/2,   p(y) = 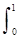(x+y) dx = y+1/2.  p(x,y) ¹ p(x)×p(y).  Величины Х и Y зависимы.

Условные плотности вероятностей по (8.4.5):  p(x/y) = (x+y)/(y+0.5),   p(y/x) = (x+y)/(x+0.5).

Моменты систем случайных величин. Вычисление моментов случайных величин с использованием многомерной плотности вероятностей может производиться как по отдельным величинам X_i, так и на любые их комбинации (смешанные моменты). Так, вычисление средних значений и дисперсий любых случайных величин, входящих в n-мерную систему, производится по формулам:

=...x_i p(x₁,x₂,...,x_n) dx₁dx₂...dx_n,                    (8.4.10)

s_xi² =... (x_i-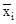)² p(x₁,x₂,...,x_i) dx₁dx₂...dx_n.          (8.4.11)

            Для случайных дискретных величин интегрирование соответственно заменяется суммированием, а плотности распределения вероятностей на распределения вероятностей.

Ковариация и корреляция. Смешанные начальные моменты второго порядка носят название ковариационных моментов системы случайных величин. Для двумерных систем:

     R₁₂ = M{X₁X₂}= =x₁x₂ p(x₁,x₂) dx₁dx₂.          (8.4.12)

В общем случае, для n-мерной системы случайных величин:

 R_ij = M{X_iX_j}= =...x_ix_j p(x₁,x₂,...,x_n) dx₁dx₂...dx_n,   i,j = 1...n     (8.4.13)

Значения моментов R_ij образуют матрицу размером n ´ n попарной ковариации всех случайных величин, входящих в систему. С учетом того, что имеет место равенство R_ij = R_ji, ковариационная матрица (см. пример) симметрична относительно главной диагонали i = j, при этом ковариационные моменты на главной диагонали матрицы представляют собой средние значения квадратов случайных величин X_i,  т.к. = R_ij  при i = j.

Смешанные центральные моменты второго порядка называют корреляционными моментами системы случайных величин. Они, как и ковариационные моменты, также образуют матрицу моментов системы, симметричную относительно главной диагонали, при этом значения моментов на главной диагонали представляют собой значения дисперсий s_i² = K_ij при i = j  соответствующих случайных величин X_i (см. пример).

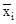K_ij = M{(X_i-)(X_j-)}=...(x_i-)(x_j-) p(x₁,x₂,...x_n) dx₁dx₂...dx_n     (8.4.14)

Корреляционные моменты является количественной мерой степени статистической связи (взаимной зависимости или корреляции) случайных величин Х_i и Х_j. Для системы случайных некоррелированных величин матрица корреляционных моментов является диагональной матрицей дисперсий с нулевыми значениями K_ij при i ¹ j (см. пример матрицы s_i²).

Из выражений (8.4.13) и (8.4.14) следует достаточно простая связь между ковариационными и корреляционными моментами:

K_ij = R_ij - ×.

В качестве безразмерной нормированной характеристики степени корреляции случайных величин используют также понятие коэффициентов корреляции, которые также образуют симметричную относительно главной диагонали матрицу со значениями, равными 1, по главной диагонали:

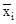
r_ij = K_ij /(s_is_j) = (-)/s_is_j.                                  (8.4.15)

Значения коэффициентов корреляции заключены в пределах от -1 до +1. При r = 0 случайные величины считаются независимыми друг от друга (например, величины (Х,Y) на рис. 8.4.1), при |r| = 1 - полностью коррелированными (например, величины Х = b×Y с произвольным значением коэффициента b), во всех остальных случаях чем ближе значение |r| к 1, тем больше корреляция между случайными величинами, которая может иметь как прямой, так и обратный характер (при r<0). Величины Х и Y на рис. 8.4.5 явно коррелированны между собой с определенным коэффициентом прямой корреляции.

Попутно заметим, что если коэффициенты корреляции статистически независимых случайных величин всегда равны нулю, то обратное утверждение о статистической независимости случайных величин, если равен нулю их коэффициент корреляции, справедливо только для гауссовских распределений, а в общем случае является недостаточным. Полную гарантию статистической независимости дает только выполнение условия (8.4.9).

С учетом выражения (8.4.9) смешанные моменты статистически независимых случайных величин разделяются на произведения интегральных сомножителей. В частности, для ковариационных моментов случайных двумерных величин имеем:

M{X₁X₂} =  x₁ p₁(x₁) dx₁  x₂ p₂(x₂) dx₂ = M{X₁}M{X₂},         (8.4.16)

т.е. математическое ожидание произведения двух статистически независимых случайных величин равно произведению их математических ожиданий. Если математическое ожидание хотя бы одной из случайных величин будет равно нулю, то нулю становится равным и их произведение.

Пример.  Плотность вероятностей задана выражением:  p(x,y) = x+y, 0 £ x £ 1, 0 £ y £ 1.

Одномерные плотности вероятностей:  p(x)=(x+y) dy =x+1/2,   p(y)=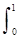 (x+y) dx = y+1/2.

Математические ожидания и дисперсии:

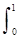=x(x+1/2) dx = 7/12,         D_x = 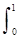(x-7/12)² (x+1/2) dx = 11/144.

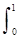=y(y+1/2) dy = 7/12,         D_y =  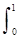(y-7/12)² (y+1/2) dy = 11/144.

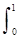
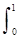= xy(x+y) dx dy = 1/3.

Коэффициент корреляции:  r_xy = (-)/s_xs_y = (1/3 - (7/12)²)/(11/144) = -1/11.

Замечание по терминологии. В современной технической литературе существует достаточно большая путаница по применению терминов ковариации и корреляции. Очень часто термин корреляции применяют как к центрированным, так и нецентрированным системам случайных величин и случайных процессов. В какой-то мере это можно считать допустимым, так как и то, и другое понятие применяется для характеристики  корреляционной связи (взаимной зависимости) случайных величин. С другой стороны, матрицу смешанных центральных моментов второго порядка так же часто называют матрицей ковариации, и т.п.

Во избежание дальнейшей путаницы в понятиях примем за основу следующее. Однозначно понимаемым и повсеместно принятым термином теории вероятностей и математической статистики является коэффициент корреляции, который вычисляется по формуле (8.4.15) с использованием центральных моментов. А потому представляется логичным именно матрицу смешанных центральных моментов и смешанные моменты второго порядка центрированных случайных величин называть корреляционными, а смешанные начальные моменты нецентрированных случайных величин - ковариационными. Такой подход применен, например, в работе /л4/ и показал себя весьма эффективным в строгой логике математических построений.

Сумма и разность случайных величин анализируются достаточно просто с предварительным вычислением одномерных плотностей вероятностей соответствующих величин по формуле (8.4.4) или с использованием непосредственно плотностей вероятностей суммируемых случайных величин, если известны только последние и неизвестна многомерная плотность вероятностей, что чаще всего и имеет место на практике.

Средние значения сумм (разностей) случайных величин вычисляются по формулам:

,                                    (8.4.17)

так как математические ожидания сумм и разностей случайных величин равны соответствующим суммам и разностям их математических ожиданий. Средние значения случайных величин вычисляются по одномерным плотностям вероятностей.

 Дисперсия суммы (разности) случайных величин может быть получена с использованием выражений, следующих из (8.3.9') и (8.4.15):

= s_x² + ,       =+ r_xy s_x s_y

Применяя эти выражения при вычислении среднего значения квадрата суммы (разности) двух случайных величин, получаем:

= ± 2+= s_x² + ± 2± 2 r_xy s_x s_y + s_y² + =

s_x² + s_y² ± 2 r_xy s_x s_y + (± )².

            Отсюда, перенося последний член выражения в левую часть:

                                   - (± )² º (s_x±y)² = s_x² + s_y² ± 2 r_xy s_x s_y.             (8.4.18)

            Если случайные величины не коррелированны, то дисперсия их суммы или разности равна сумме их дисперсий.

            Плотность вероятностей суммы (разности) случайных величин по известным плотностям вероятностей суммируемых величин в общем случае определяется достаточно сложно. Задача значительно облегчается, если случайные величины статистически независимы. Рассмотрим этот случай на примере случайной двумерной величины Z=X+Y с известными плотностями вероятностей p_x(x) и p_y(y).

            Совместная плотность вероятностей p(z) = p(x,y) определяет функцию распределения вероятностей P(z) = P(Z £ z) = P(X+Y  £  z), причем для каждой совместной реализации имеем z=x+y и, соответственно, x=z-y и y=z-x. Отсюда, с учетом статистической независимости случайных величин X и Y, и, соответственно, p(x,y) = p_x(x)×p_y(y), для распределения вероятностей P(z) имеем:

                                P(z) = p(x,y) dx dy = p_y(y) p_x(x) dx dy.            (8.4.19)

            Продифференцируем данное выражение по z и, поскольку переменная z присутствует только в верхнем пределе второго интеграла, получим:

                                 d P(z)/dz º p(x,y) =p_y(y) p_x(z-y) dy º p_y(y) _* p_x(z-y).             (8.4.20)

            Аналогично, если принять y=z-x в качестве верхнего предела во втором интеграле выражения (8.3.19), можно получить:

                                       p(x,y) =p_x(x) p_y(z-x) dx º p_x(x) _* p_y(z-x).                        (8.4.20')

            Таким образом,  двумерная плотность вероятностей суммы случайных величин равна свертке их одномерных плотностей распределения вероятностей.

            Для разности случайных величин Z=X-Y в выражении (8.3.19) верхний предел заменяется соответственно на z+y, при этом:

                                   p(x,y) =p_y(y) p_x(z+y) dy ºp_y(x-z) p_x(x) dx.                   (8.4.21)

            Сумма и разность нормальных распределений. Плотность вероятностей суммы Z=X+Y двух нормальных распределений случайных величин X и Y получается непосредственной подстановкой выражений гауссовских распределений (8.3.15) в (8.4.20):

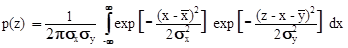
                                               .                       (8.4.22)

Бесплатная лекция: "7 Основной вопрос философии, его структура" также доступна.

            Аналогично для разности двух случайных величин Z=X-Y:

                                               .                        (8.4.23)

            Как видно из полученных выражений, сумма и разность двух независимых нормально распределенных случайных величин также распределена нормально с дисперсией, равной сумме дисперсий исходных случайных величин, и со средними значениями, соответственно равными сумме и разности средних значений исходных величин.    На рис. 8.4.6 в качестве примера приведены графики нормальных распределений случайных величин X (=4, s_x=0.5), Y (=2, s_y=0.4) и  Z=X+Y,  N=X-Y.

            Эти выводы действительны для сумм и разностей произвольного количества нормально распределенных случайных величин в любых сочетаниях и результатом  всегда будет случайная величина с нормальной плотностью распределения вероятностей. Это свойство называется устойчивостью закона распределения случайной величины, и оно является достаточно редким. Для гауссовских распределений это свойство сохраняется даже для коррелированных случайных величин, естественно с определением дисперсии по выражению (8.4.18). А так как функция распределения Гаусса относится к числу собственных, то функции дифференцирования, интегрирования и других линейных преобразований гауссовского распределения также являются нормальными.