Преобразование СП-структур

3.5. Преобразование СП-структур

3.5.1. Общие положения

Реально отображение одного и того же объекта может представляться различными СП-структурами. Каждую новую СП-структуру можно рассматривать как результат преобразования некоторой исходной СП-структуры. Преобразования, которые могут претерпевать СП-структуры, будем называть допустимыми. Множество всех допустимых преобразований обычно образует группу допустимых преобразований.

 Если группа допустимых преобразований определена, то множество всех СП-структур одного и того же объекта, получающихся при всех допустимых преобразованиях, образует класс эквивалентности. После того, как в каждом классе выделен представитель (эталонная СП-структура) можно говорить о двух задачах в распознавании СП-структур. Первая задача состоит в том, чтобы по данной СП-структуре определить класс эквивалентности, которому она принадлежит, т.е. найти те признаки, которые позволяют отделить один класс от другого. Поскольку признаки вычисляются на основе данной СП-структуры, но характеризуют классы СП-структур, то они должны быть инвариантными по отношению к допустимым преобразованиям. Поэтому первая задача состоит в том, чтобы по данной СП-структуре вычислить весь ряд инвариантов (инвариантных признаков), позволяющих определить класс, к которому принадлежит СП-структура.

Вторая задача состоит в том, чтобы по данной СП-структуре определить то преобразование, которому была подвергнута исходная СП-структура. Иногда вторую задачу можно сформулировать следующим образом: даны две эквивалентные СП-структуры; требуется определить допустимое преобразование, переводящее одну СП-структуру в другую.

Обозначим через G группу допустимых преобразований СП-структур. Каждая СП-структура описывается матрицей инцидентности D и вектором начальной разметки m0 . Преобразование СП-структур рассматривается как преобразование D и m0 . Если g О G - допустимое преобразование, то будем обозначать через g(D, m0) матрицу инцидентности и вектор начальной разметки преобразованной СП-структуры.

Инвариантом будем называть такую функцию J(D, m0), которая сохраняется при применении к СП-структуре любого допустимого преобразования:

 J(D, m0) = J (g(D, m0)), "g О G, " (D, m0) .

Рекомендуемые материалы

 Первая задача распознавания состоит в том, чтобы найти полную систему признаков, т.е. семейство инвариантов {Ja} , которое позволяет различать СП-структуры разных объектов. Иначе говоря, полнота системы признаков {Ja} означает, что все признаки двух СП-структур N и N' совпадают тогда и только тогда, когда СП-структуры эквивалентны, т.е. существует допустимое преобразование g О G, переводящее СП-структуру N в СП-структуру N':

            (Ja(N) = Ja(N'), "a )   «   ($g  О G , g(N) = N') .

 Вторая задача распознавания состоит в том, чтобы для двух эквивалентных СП-структур - исходной N  и преобразованной N' , найти допустимое преобразование g , которое переводит N в N' :

g(N) = N' .

Если преобразование g не единственное, то надо найти все g, переводящие  N в N' .

Пусть Go - некоторая подгруппа группы допустимых преобразований G . Пусть для любой СП-структуры N задано допустимое преобразование gr О G , переводящее N в некоторую СП-структуру NR :

gr (N) = NR .

При этом преобразования gr таковы, что любые две СП-структуры N и, эквивалентные относительно полной группы допустимых преобразований G , переходят в СП-структуры NR и  , эквивалентные относительно группы G0 :

($gr О G, gr(N) = ) ® ($g0 О G0, g0(NR) = ).                      (3.8)

Такие преобразования gr будем называть преобразованиями редукции, а преобразованные СП-структуры NR - редуцированными. Подгруппу G0 будем называть подгруппой редукции.

Пусть мы умеем решать обе задачи распознавания для подгруппы допустимых преобразований G0 на множестве редуцированных СП-структур. Это означает, что, во-первых, у нас есть полная система инвариантных признаков  таких, что

 =  , "a, "g0 О G0 ,

и                                 ( = , "a) ® ($g0 О G0 ,  = g0(NR)) ,

а, во-вторых, для любых редуцированных СП-структур NR и , у которых совпадают эти признаки,

 =  , "a,                                     (3.9)

мы можем находить преобразование go О Go такое, что g0(NR) =  .

Нетрудно видеть, что редукция СП-структур сохраняет отношение эквивалентности по группе G .

Утверждение 3.3. Две СП-структуры N и  эквивалентны относительно полной группы допустимых преобразований G тогда и только тогда, когда их редуцированные СП-структуры NR и  эквивалентны относительно подгруппы допустимых преобразований G0 (подгруппы редукции).

В прямую сторону это утверждение верно в силу выражения (3.8), а в обратную - оно следует из того, что преобразования редукции по определению являются допустимыми: {gr , } М G , поэтому, если  = g0(NR) , g0 = G , то = g(N) , причем

g =  ° g0 ° gr О G .

 Если редукция СП-структур определена, то две задачи распознавания для полной группы допустимых преобразований G решаются следующим образом. Полная система инвариантов строится так:

Ja(N) =  , "a,                                          (3.10)

т.е. значение инвариантного признака Ja для СП-структуры N равно значению признака  для редуцированной СП-структуры.

Докажем, что Ja являются инвариантными для группы G. Возьмем любую СП-структуру N и любое преобразование g О G. Обозначим через  преобразованную СП-структуру:

                                                            = g(N) ,

а NR и  - редуцированные СП-структуры. СП-структуры N и  эквивалентны по группе G , поэтому по определению редукции СП-структуры NR и  эквивалентны по группе G . Следовательно, у них совпадают все признаки , т.е. выполнено (3.9). Но тогда из (3.10) следует: Ja(N) = Ja(), "a , что и требовалось доказать.

3.5.2. Операции преобразования СП-структур

Для проведения автоматизированного анализа и синтеза ВС необходимы средства, позволяющие преобразовывать СП-структуры ВС. С этой целью рассмотрим операции преобразования, которые включают операции разделения и объединения вершин, введенные в параграфе 3.1.

Множественное разделение вершин СП-структур. Взаимодействие процессов параллельных ВС моделируется СП-структурами путем ввода вершин, имеющих несколько входных или несколько выходных дуг. Поэтому анализ ВС, т.е. выделение множества взаимодействующих процессов, проводится путем деления подобных вершин до получения линейных или линейно-циклических фрагментов, составляющих исходную СП-модель. Рассмотрим правила множественного деления позиций и переходов СП-моделей.

Следует отметить, что при определении вершин, которые должны подвергаться делению, вес дуг не учитывается. Данное требование вводится с целью сохранения свойства замкнутости операций разделения и объединения в пределах заданного пространства. Делению подвергаются вершины, которые удовлетворяют следующим условиям:

|pre(t)| + |post(t)| > 2 ,                                                (3.8)

|pre(p)| > 1 или |post(p)| > 1 .                                   (3.9)

Рассмотрим типы вершин СП-структур, удовлетворяющих условиям (3.8) и (3.9).

Множественное разделение переходов СП-структур. В данном пункте будем рассматривать вершины СП-структур, которые удовлетворяют условию (3.8). Физический смысл данных вершин заключается либо в синхронизации n параллельно протекающих процессов, либо в активизации m параллельных процессов. Данные процессы могут быть выделены путем разделения перехода ti на m переходов. Один из вариантов деления представлен на рис.3.3.

Рассмотрим более сложный тип вершины, представленный на рис. 3.4. Физический смысл данной вершины заключается в синхронизации n параллельно протекающих процессов и активизации новых m параллельных процессов, т.е. данная вершина может быть представлена, как показано на рис.3.4,б, из которого видно, что завершение n процессов порождает m новых параллельных процессов. Отсюда следует, что деление подобных структур можно проводить по вершине p (рис.3.4,в), что приводит к получению структур, описанных выше. Такой способ деления переходов будем называть горизонтальным делением.

Другой способ деления подобных вершин (вертикальное деление) представлен на рис.3.5. Данный вариант деления учитывает случай, когда n > m. Если соотношение между входным и выходным множествами позиций определяется неравенством n < m , то деление структуры, представленной на рис.3.5, осуществляется аналогично.

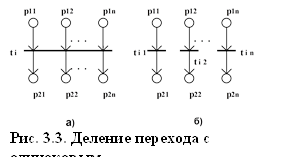
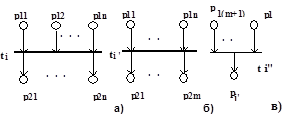
Рис. 3.5. Вертикальное деление перехода

Вертикальный способ деления применяется при выделении максимально длинных последовательностей процессов. Так как переход ti моделирует процедуру синхронизации и активизации n новых процессов, то, очевидно, при разделении данной вершины на последовательные процессы безразлично, какой новый процесс будет следовать за ранее протекавшим. Поэтому сочетание входных и выходных позиций при делении перехода ti может быть произвольным.

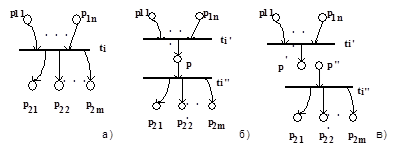
Рис. 3.4. Горизонтальное деление перехода

Сформулируем правила выполнения операций деления переходов.

Определение 3.8 (множественное деление перехода с выходной позицией).

 Если для перехода ti выполняются условия: pre(ti)={pi1, pi2,..., pin} и post(ti)={pj}, то переход ti делится на n переходов (ti1, ti2,..., tik,..., tin ), для которых справедливо:

pre(tik ) = {pik}, post(tik) = {pj}, где 1 <= k <= n .

Определение 3.9 (множественное деление перехода с входной позицией). Если для перехода ti выполняются условия:

 pre(ti) = {pj} и post(ti) = {pi1, pi2,..., pin}, то данный переход делится на n переходов (ti1, ti2,..., tik,..., tin), для которых справедливо:

pre(tik) = {pj}, post(tik) = {pik}, где 1 <= k <= n .

Определение 3.10 (множественное деление перехода с одинаковым числом входных и выходных позиций). Если для перехода ti выполняются условия:

pre(ti)={p11, p12,..., pn} и post(ti) = {p21, p22,..., p2n}, то данный переход делится на n переходов (ti1, ti2,..., tin ), для которых справедливо:

pre(tik) = {p1k}, post(tik) = {p2k} , где 1 <= k <= n .

Определение 3.11 (горизонтальное деление перехода). Если для перехода ti выполняются условия pre(ti)={p11, p12,..., p1n} и post(ti) = {p21, p22,..., p2m}, то переход ti делится на переходы: ti' - с выходной позицией p’ и ti'' - с входной позицией p’’, для которых справедливо:

pre(ti') = pre(ti) , post(ti') = {p'} ,

pre(p') = {ti'}, post(p') = Ж , m(p') = 0

и pre(ti'') = {p''} , post(ti'') = post(ti) ,

pre(p'') = Ж , post(p'') = {ti''}, m(p'') = 0 .

Определение 3.12 (вертикальное деление перехода). Если для перехода ti выполняются условия pre(ti ) = {p11, p12 ,...,p1n } и post(ti ) = {p21, p22, ..., p2m },

а) n > m , то переход ti делится на переходы ti ' и ti '', для которых справедливо:

 pre(ti ') = {p11, p12,..., p1m} ,

 post(ti ') = {p21, p22,...,p2m}

 pre(ti '') = {p1(m+1),..., p1n } , post(ti'') = {pj'} ,

 pre(pj') = {ti''}, post(pj') = Ж , m(pj') = 0;

б) m > n , то перход ti делится на переходы ti' и tj'', для которых справедливо:

 pre(ti ') = {p11, p12,..., p1n } , post(ti') = {p21, p22,..., p2n },

 pre(ti '') = {p j '} , post(ti '') = {p2(n+1),..., p2m } ,

 pre(pj') = Ж , post(pj') = {ti''} , m(pj') = 0.

Множественное разделение позиций СП-структур.В данном пункте будем рассматривать вершины СП-моделей, которые удовлетворяют условию (3.9). Рассмотрим вершины, представленные на рис.3.6 и рис.3.7. В дальнейшем данные вершины будем называть головной позицией (рис.3.6,a) и хвостовой позицией (рис.3.7,a). Физический смысл вершины, представленной на рис.3.6, заключается в выборе альтернативного процесса из возможных, т.е. данная

  

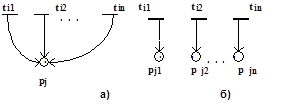
     Рис. 3.6. Деление головной позиции                        Рис. 3.7. Деление хвостовой позиции

вершина описывает некоторое устройство выбора в ВС. Поэтому при выделении процессов, протекающих в параллельной ВС, данная вершина преобразуется к виду, представленному на рис.3.6,б. На рис.3.7,а представлена вершина, моделирующая слияние альтернативно протекающих процессов. Выделение данных процессов также соответствует разделению позиции pi на n позиций (рис.3.7,б). Рассмотрим вершину, представленную на рис.3.8,а. Данная вершина объединяет две вершины, представленные на рис.3.6,а и рис.3.7,а, в одну. Особенностью данной вершины является равенство числа входных и выходных переходов. Выделение взаимодействующих процессов в этом случае можно провести путем разделения вершины pi на фрагменты, показанные на рис.3.8,б.

            Рассмотрим более сложный тип вершины, который представлен на рис.3.9. Горизонтальное деление позиции (рис.3.9,б) физически означает выделение блоков устройства, которые обеспечивают формирование условий завершения альтернативно протекающих процессов и формирование условий для активизации следующего процесса, также принадлежащего множеству альтернативно протекающих процессов. Вертикальное деление позиции (рис.3.10) сводится к получению известных структур, представленных на рис.3.6,а и рис.3.8,а. Данный вариант деления учитывает случай, когда n > m . Если соотношение между входным и выходным множеством переходов определяется неравенством m > n, то деление позиции pi осуществляется на фрагменты, представленные на рис.3.7,а и рис.3.8,а.

Сформулируем правила выполнения операций деления позиций.

Определение 3.13. Множественное деление головной позиции. Если для позиции pj выполняются условия: pre(pj) = Ж , и post(pj) = {ti1, ti2, ..., tin }, то позиция pj делится на n позиций (pj1, pj2, ..., pjk, ..., pjn), для которых справедливо:

pre(pjk) = Ж , post(pjk) = {tik}, m(pjk) = m(pj) , где 1 <= k <= n .

Определение 3.14. Множественное деление хвостовой позиции. Если для позиции pj выполняются условия: pre(pj )={ti1, ti2, ..., tin} и post(pj) = Ж , то позиция pj делится на n позиций (pj1, pj2, ..., pjk, ..., pjn), для которых справедливо:

pre(pjk) = {tik} , post(pjk) = Ж , m(pjk) = m(pj) , где 1 <= k <= n .

Определение 3.15. Множественное деление позиции с одинаковым числом входных и выходных позиций. Если для позиции pj выполняются условия: pre(pj) = {t11, t12,..., t1n } и post(pj) = {t21, t22,..., t2n }, то данная позиция делится на n позиций (pj1, pj2,..., pjn ), для которых справедливо: pre(pjk) = {t1k} , post(pjk) = {t2k} , где 1<=k<=n.

Определение 3.16. Горизонтальное деление позиции. Если для позиции pj выполняются условия:

pre(pj) = {t11, t12,..., t1n} и post(pj) = {t21, t22,..., t2m}, то позиция pj делится на хвостовую (pj') и головную (pj'') позиции, для которых справедливо:

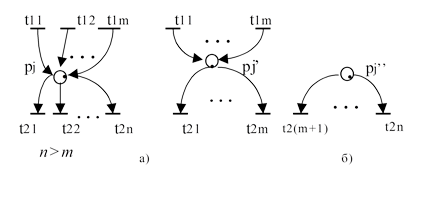pre(pj ') = pre(pj ) , post(pj ') = Ж , m(p j ') = 0 , и pre(pj '') = Ж , post(pj '') = post(pj ), m(pj '') = m(pj) .

Определение 3.17. Вертикальное деление позиции. Если для позиции pj выполняются условия:

Вам также может быть полезна лекция "2 Администрирование информационных сетей".

pre(pj) = {t11, t12,..., t1m} , post(pj) = {t21, t22,..., t2n} и

а) n > m , то позиция pj делится на позиции pj ' и pj '' , для которых справедливо:

pre(pj ') = {t11, t12,..., t1m } , post(pj') = {t21, t22,..., t2m},

m(pj ') = m(pj ) , pre(pj '') = Æ , post(pj '') = {t2(m+1),..., t2n},

m(pj '') = m(pj ) ;

б) n < m, то позиция pj делится на позиции pj ' и pj '', для которых справедливо: pre(pj ') = {t11, t12,..., t1n}, post(pj') = {t21, t22,..., t2n}, m(pj ') = m(pj ), pre(pj '') = {t1(n+1),..., t1m}, post(pj'') = Ж , m(pj'') = m(p j ) .