Нейронный контроллер

МЕТОДЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА

ЛЕКЦИЯ № 9

На прошлой лекции мы рассмотрели общие схемы нейросетевого управления, которые предлагает г-н Омату, поставили задачу и посмотрели, что там внутри у нейроэмулятора.

Сегодня мы посмотрим, что внутри у нейроконтроллера, а также займёмся повышением эффективности оперативного управления.

Нейронный контроллер

Предположим, что объект управления, описываемый уравнением,  является обратимым. То есть существует функция , такая, что

.

Рассмотрим многослойную нейронную сеть с -мерным вектором входов , одним входом  и соотношением между входом и выходом, кратко описываемым следующим образом:

Рекомендуемые материалы

,

где

 — отображение вход/выход многослойной нейросети.

Если выход  близок к выходу  при соответствующих входах, то многослойная нейросеть может рассматриваться как контроллер в прямой цепи управления. В момент времени  значение входа объекта управления можно получить с помощью выражения , подставив в него:

.

Обратите внимание, что здесь вместо неизвестной величины  использовано значение опорного сигнала . Если ошибка выхода  поддерживается на достаточно низком уровне после окончания процесса обучения, можно использовать значения опорного сигнала вместо у:

.

Отсюда видно, что нейроконтроллер не имеет обратных связей, как в последовательной схеме нейронного управления.

Эффективное оперативное управление

Медленная сходимость обучения — основной недостаток многослойных нейросетей, серьёзно ограничивающий практическое применение нейронного управления. Существует несколько подходов для ускорения сходимости в нейронном управлении. Перечислим некоторые из них.

1. Разработка эффективных алгоритмов обратного распространения.

2. Встраивание знаний о структуре объекта управления в структуру многослойных нейросетей.

3. Применение гибридных сетей, в которых искусственные нейросети связываются со структурами управления, полученными на основе других, отличных от нейронных, технологий.

4. Предварительное обучение и эффективные процедуры инициализации.

Далее мы рассмотрим новые алгоритмы оперативного обучения, направленные на сокращение времени обучения нейроконтроллеров. Эти алгоритмы основаны на разделении понятий частоты дискретизации и частоты выполнения обучающих итераций (частоты обучения). В системах управления с дискретным временем период дискретизации Т обычно выбирается по следующему эмпирическому правилу: величина  должна значительно превышать максимальную частоту, имеющуюся в системе с непрерывным временем. Обычно повышение частоты дискретизации улучшает характеристики системы, однако это улучшение быстро прекращается (график изменения характеристик достигает плато). В обычных адаптивных системах управления адаптивные элементы, как правило, корректируются один раз за каждый период дискретизации; таким образом, частоту дискретизации и частоту обучения можно не различать. Если пренебречь ограничениями на время обработки, то может показаться, что фактическое время обучения можно сократить, повысив частоту дискретизации.

Однако во многих практических случаях превышение некоторого предела частоты дискретизации недопустимо или нежелательно. Например, в обычных промышленных химических установках, как правило, интерес представляют процессы, связанные с большими величинами временных констант. При этом не имеет смысла использовать высокие частоты дискретизации: это может привести к избыточности информации. Использование очень высоких частот дискретизации может привести к полной перестройке системы управления и усложнить её. Может потребоваться учитывать частные процессы и переходные явления, которые при меньших частотах дискретизации можно было бы игнорировать.

Другой пример систем, в которых нельзя использовать произвольно высокую частоту дискретизации — распределённые системы управления, в которых интервалы передачи информации на устройство управления и приёма информации с него не зависят от самого устройства управления.

Хотя период дискретизации Т задаёт базовый темп работы системы управления, в системах с итерационным обучением частота обучающих операций может рассматриваться как ещё одна основа для отсчёта времени. На практике период дискретизации Т обычно значительно превышает время , затрачиваемое на одну обучающую итерацию, то есть на корректировку всех весов сети. По мере появления многослойных сетей с более высоким быстродействием (за счёт улучшения их программной или аппаратной реализации) отношение  повышается.

Таким образом, если имеется соответствующая информация о входе и выходе объекта управления, и интерес представляет только время, то за период дискретизации может выполняться несколько обучающих итераций. Обычный (и самый простой) подход состоит в выполнении одной корректировки за период дискретизации, и он связан с непроизводительными затратами времени обработки. Проблема состоит в том, каким образом выбрать и использовать обучающие данные, и как использовать имеющееся время для рационального обучения нейросетей, т.е. для обучения, которое должно повысить эффективность управления.

Г-н Омату предлагает три метода обучения, в которых за каждый период дискретизации выполняется несколько обучающих итераций.

1. Обучение эмулятора

Предположим, что в момент времени  в памяти хранится текущее значение выхода ,  значений того же процесса в предшествующие моменты времени и  значений входного процесса  в предшествующие моменты времени. В этом случае в качестве образцов для обучения эмулятора в момент времени  могут использоваться  пар , . Для случая  требуется минимизировать следующую функцию ошибки:

,

где

 — невозрастающая положительная последовательность, предназначенная для определённого „забывания“ образцов, полученных ранее.

Пример. Пусть только что получена величина  (т.е. величина  ещё не известна), , , . Предположим также, что величины , , …  и , …  имеются в памяти. В этом случае выходные векторы эмулятора можно представить в виде:

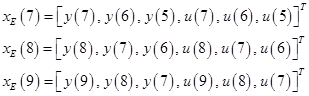
Эти выходные векторы и величины  образуют обучающие образцы для обучения в момент времени . Эту процедуру можно представить в виде рисунка.

{рисунок 4.4.1-а, с. 127}

Здесь через  обозначено состояние эмулятора во время -го интервала дискретизации, после -й обучающей итерации, . Аналогично  обозначает отображение вход/выход, выполняемое эмулятором в состоянии . Очевидно, что .

2. Обучение контроллера: подход на основе ошибки инверсно-прямого управления

Вспомним инверсно-прямую конфигурацию управления (рис. 4.3.10, с. 112). Предположим то же самое: что в момент времени t+1 в памяти хранится текущее значение выхода ,  предыдущих значений выходного и  значений входного процессов. В этом случае в качестве образцов для обучения нейроконтроллера в момент времени t+1 могут использоваться n пар

, i=0…n-1,

при этом

.

При , и функция ошибки

.

И соответствующий -член для -го образца записывается следующим образом:

.

Следует отметить, что функция ошибки  не включает в себя непосредственно координату ошибки объекта управления. В связи с этим обучение объекта управления непосредственно не повышает эффективность управления. Однако такой способ обучения позволяет достичь хорошего обобщения в пространстве параметров управления. На практике обучение нейроконтроллеров, основанное только на инверсно-прямом подходе, даёт плохие результаты: выход нейроконтроллера устанавливается на некоторой постоянной величине, в результате чего ошибка обучения оказывается нулевой, однако характеристики управления оказываются явно плохими. Этот недостаток присущ всем методам обучения, основанным на минимизации ошибки инверсного управления. Его можно устранить, используя сочетание таких методов управления с другими, непосредственно минимизирующими ошибку системы регулирования.

И вот пример, который это иллюстрирует.

Пусть р=3, q=2 и только что получена величина у(9). Предположим также, что в памяти имеются аналогичные величины, что и в предыдущем примере: , , …  и , … .

Обозначим через  текущее отображение, выполняемое нейроконтроллером. Равенство  означает, что обучения ещё нет. Входной сигнал для объекта управления  можно вычислить из соотношения , где .

Люди также интересуются этой лекцией: Лекция 10.

Для обучения в соответствии с подходом на основе ошибки инверсно-прямого управления можно использовать следующие векторы:

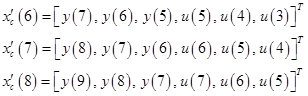
Эти векторы и входные величины ,  и  образуют три обучающих образца (входной вектор и желаемый выход) для обучения нейроконтроллера в момент времени . Однако такой метод обучения непосредственно не минимизирует ошибку управления, поэтому на практике необходимо его сочетание с другими методами.

На рисунке этот подход будет выглядеть так:

{рис. 4.4.1-б, с. 127}

На рисунке показано сочетание множественного обучения на основе инверсно-прямого управления и простого обучения на основе обучающей конфигурации. В результате выполняется 4 обучающих итерации за один период дискретизации. Вектор хс(8) задаётся составляющими . Через  обозначено состояние нейроконтроллера во время -го интервала дискретизации, после -й обучающей итерации. В результате достигается точное обучение нейроэмулятора за счёт усложнения процесса обучения.