Алгоритмы обучения

МЕТОДЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА

ЛЕКЦИЯ № 10

На прошлой лекции мы начали заниматься проблемой эффективного управления с помощью нейроконтроллеров. Я напомню, г-н Омату предлагает три метода обучения. Первый — это обучение эмулятора, а другие два — это обучение контроллера, либо на ошибке инверсно-прямого управления, либо на основе прогнозируемой ошибки выхода.

Мы остановились на втором подходе, и пришли к выводу, что он сам по себе даёт плохие результаты: выход нейроконтроллера устанавливается на некоторой постоянной величине, в результате чего ошибка обучения оказывается нулевой, однако характеристики управления оставляют желать лучшего. Этот недостаток присущ всем методам обучения, основанным на минимизации ошибки инверсного управления. Его можно устранить, используя сочетание таких методов управления с другими, непосредственно минимизирующими ошибку системы регулирования.

Мы начали рассматривать пример, который это иллюстрирует.

Пусть р=3, q=2 и только что получена величина у(9). Предположим также, что в памяти имеются аналогичные величины, что и в предыдущем примере: , , …  и , … .

Обозначим через  текущее отображение, выполняемое нейроконтроллером. Равенство  означает, что обучения ещё нет. Входной сигнал для объекта управления  можно вычислить из соотношения , где .

Рекомендуемые материалы

Для обучения в соответствии с подходом на основе ошибки инверсно-прямого управления можно использовать следующие векторы:

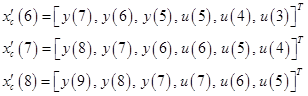
Эти векторы и входные величины ,  и  образуют три обучающих образца (входной вектор и желаемый выход) для обучения нейроконтроллера в момент времени . Однако такой метод обучения непосредственно не минимизирует ошибку управления, поэтому на практике необходимо его сочетание с другими методами.

На рисунке этот подход будет выглядеть так:

{рис. 4.4.1-б, с. 127}

На рисунке показано сочетание множественного обучения на основе инверсно-прямого управления и простого обучения на основе обучающей конфигурации. В результате выполняется 4 обучающих итерации за один период дискретизации. Вектор  задаётся составляющими . Через  обозначено состояние нейроконтроллера во время -го интервала дискретизации, после -й обучающей итерации. В результате достигается точное обучение нейроэмулятора за счёт усложнения процесса обучения.

3. Обучение контроллера: подход на основе прогнозируемой ошибки выхода

Более сложный подход к множественному обучению нейроконтроллера можно получить на основе конфигурации из эмулятора и контроллера (рис. 4.2.5, с. 98). Предположим, что в момент времени  в дополнение к  значениям переменной  (включая ) и  предыдущим значениям переменной     имеется также  значений опорного сигнала .

 Наличие таких данных эквивалентно наличию в памяти  входных векторов . В момент времени  входной управляющий сигнал  определяется следующим образом:

.

Однако с момента времени, когда вектор  был сохранён, до текущего момента времени  было выполнено несколько корректировок нейроконтроллера. Поэтому в момент времени  сохранённый входной вектор  даст следующий виртуальный входной сигнал:

.

Это означает только, что последняя величина  с соответствующими величинами  и   может быть непосредственно использована для обучения на основе одной из конфигураций адаптивного управления. Однако это не относится в полной мере к предыдущим величинам  для . Для таких случаев можно спрогнозировать соответствующий выходной сигнал объекта управления с помощью эмулятора в соответствии с выражением:

,

где второй верхний индекс в обозначении  опущен для простоты, а вектор  задаётся следующим образом:

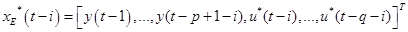
{рис. 4.4.2-а, с. 130}

Для лучшего понимания процесса обучения нейроконтроллера представим себе нейроконтроллер и нейроэмулятор как одну многослойную сеть. В момент времени  каждому входному вектору  пусть соответствует прогнозируемая ошибка , и обучение направлено на минимизацию некоторой нормы предсказанной ошибки выхода. Функция ошибки может иметь следующий вид:

.

В обучающей конфигурации нейроконтроллер обучается на основе ошибки, представляющей собой расхождение между опорным сигналом и выходом нейроэмулятора, а не расхождение между опорным сигналом и выходом объекта управления, как в схеме прямого адаптивного управления. Предыдущие значения величины выхода объекта управления  необходимы для входных векторов нейроконтроллера и нейроэмулятора.

Пример. Пусть ,  и только что получена величина . Предположим, что в памяти имеются значения , а также , и ещё ,  и . Входные векторы нейроконтроллера, используемые для вычисления трёх последних значений входного управляющего сигнала, можно записать в следующей форме:

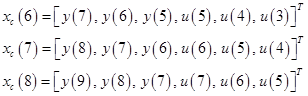
Возможная процедура обучения для момента времени  показана на следующем рисунке:

{рис. 4.4.2-б, с. 130}

За один период дискретизации выполняется три обучающих итерации.

Мы сейчас рассмотрели методы оперативного обучения, предложенные г-ном Омату. А теперь мы рассмотрим, в теории, алгоритмы в псевдокоде, который обеспечит определённую однозначность реализации таких методов.

Алгоритмы обучения

Сперва обращу внимание, что алгоритм обратного распространения мы будем указывать в виде вызова процедуры ,

где  — это имя процедуры,  — корректируемая сеть,  — входной вектор,  — желаемый выход, а  — фактический выход.

1. Множественное обучение эмулятора

Пусть в момент времени  в памяти хранятся векторы  для . Из этого следует, что новейшие данные соответствуют значению , а более старые данные соответствуют большим значениям . Начиная с момента времени , алгоритм множественного обучения эмулятора можно представить в следующей форме.

Шаг 1.

read ;

Шаг 2. {Обучение эмулятора}

for :=() downto 0 do

begin

    :=;

    ;

end;

Шаг 3. {Генерация управляющего входного сигнала}

:=;

или

:=;

:=;

Шаг 4. Применить  к объекту управления и ждать время .

Шаг 5. {Сдвиг данных}

for :=() downto 1 do

    :=;

Шаг 6. {Новейший вектор данных}

:=;

Шаг 7.

:=;

Шаг 8. Переход к шагу 1.

2. Множественное обучение контроллера: инверсно-прямое управление

Пусть в момент времени  в памяти хранятся векторы  для . Начиная с момента времени , алгоритм множественного обучения контроллера можно представить в следующей форме.

Шаг 1.

read ;

Шаг 2. {Новейший вектор данных}

:=;

Шаг 3. {Обучение контроллера}

for :=() downto 0 do

begin

    :=;

    ;

end;

Шаг 4. {Генерация управляющего входного сигнала}

:=;

или

:=;

:=;

Шаг 5. Применить  к объекту управления и ждать время .

Шаг 6. {Сдвиг данных}

for :=() downto 1 do

    :=;

Шаг 7.

:=;

Шаг 8. Переход к шагу 1.

3. Множественное обучение контроллера: прогнозируемая ошибка выхода

Пусть в момент времени  в памяти хранится -вектор  или . Обозначим через  нейронные сети, образованные связыванием нейроконтроллера и нейроэмулятора. Начиная с момента времени , алгоритм множественного обучения контроллера можно представить в следующей форме.

Шаг 1.

read ;

Шаг 2. {Обучение контроллера по прогнозируемым ошибкам}

for :=() downto 1 do

begin

    for :=0 to  do

        :=;

         {виртуальный входной вектор для эмулятора}

    :=;

         {виртуальный выход}

    :=;

         ;

end;

Шаг 3. {Обычное обучение с использованием новейших данных}

;

Шаг 4. {Сдвиг данных}

for :=() downto 1 do

    :=;

Шаг 5. {Генерация управляющего входного сигнала}

:=;

или

:=;

Люди также интересуются этой лекцией: Особенности управления основной памятью ЭВМ.

:=;

Шаг 6. Применить  к объекту управления и ждать время .

Шаг 7.

:=;

Шаг 8. Переход к шагу 1.

Сегодня мы закончили изучать методы эффективного обучения нейроэмуляторов и нейроконтроллеров, рассмотрели в теории алгоритм работы каждого из этих методов. На следующем практическом занятии мы будем изучать, как это работает с реальными цифрами.