Методологические отличия

Лекция 5

1.9 Методологические отличия

            Термин методологическое отличие используется здесь для описания особенностей системных задач, по которым раз­личаются равные типы задач внутри одного типа моделей систем. Методологические отличия касаются как систем, так и требований к ним.

Типы задач, отличающиеся только некоторыми методологическими отличиями, требуют разных мето­дов решения, но имеют один и тот же статус в иерархии типов моделей систем. Таким образом, методологические отличия представляют собой вторичные критерии классификации задач научных исследований.

В данном разделе рассматриваются методологические отличия, относящиеся к переменным и их параметрам. Так как переменные и параметры являются компонентами любой системы независимо от ее типа, эти отли­чия применимы к системам всех типов моделей.

Методологические отличия для переменных и параметров — это характеристики их множеств состояний и, соответственно, пара­метрических множеств. Если переменная (или параметр) пред­ставляет свойство (или базу), то эти свойства не могут быть про­извольными.

Всякая переменная связана с одним или несколькими парамет­рами, и изменения состояний переменной наблюдаются на полном параметрическом множестве. Таким образом, комбинация свойств множества состояний и полного параметрического множества оп­ределяет самый элементарный тип методологических отличий.

Если имеется более одного параметра, то полное параметриче­ское множество представляет собой декартово произведение от­дельных параметрических множеств. Для представления распозна­ваемых свойств этого декартова произведения, свойства отдельных параметров должны сочетаться соответствующим образом. Будем сначала для простоты считать, что мы имеем дело с од­ним параметрическим множеством независимо от того, является оно отдельным параметрическим множеством или декартовым про­изведением нескольких, и что выделенными свойствами обладают все это множество.

Рекомендуемые материалы

Одним из фундаментальных методологических отличий явля­ется отсутствие математических свойств у множества состояний или соответствующего параметрического множества. Это крайний случай, и он плохо подходит для переменной (или параметра), предназначенной для представления свойства (или базы) и имею­щей явно выраженные и существенные для задачи характеристи­ки. В литературе по измерениям переменные такого рода обычно на­зывают переменными с номинальной шкалой.

Наиболее фундаментальным из выделяемых свойств множеств состояний и параметрических множеств является упорядоченность. Методологически следует различать два типа упорядоченности — частичную и линейную.

Частичная упорядоченность — это бинарное отношение на мно­жестве (в нашем случае на множестве состояний или параметри­ческом), являющееся рефлексивным, антисимметричным и транзи­тивным. Линейная упорядоченность сильнее частичной, так как это частичная упорядоченность, обладающая свойством связности (т. е. любая пара элементов множества так или иначе упорядо­чена).

∆ Формально частичная упорядоченность Q, например, множе­ства V_i — это бинарное отношение

                                                                            Q  V_i  V_i 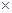,(1.11)

удовлетворяющее следующим требованиям:

1. (x, x)  Q (рефлексивность);

2.  если (x, y)  Q и(y, x)  Q, то х = у (антисимметричность);

1. если  (x, y)  Q и (y, z)  Q , то ( x, z )  Q (транзитивность).

Если (x , y)  Q то х называется предшественником у, а у — преемником х. Если (x , y)  Q и не существует, z  Q, такого, что ( x, z )  Q и (z, x)  Q, то х называется непосредственным предшественником у, а у — непосредственным преемником х. В допол­нение к требованиям рефлексивности, антисимметричности и транзитивности отношение линейной упорядоченности удовлетво­ряет следующему требованию связности: для всех х, y  V_i , если , то или (x, y)  Q или (y, x)  Q. ▲

Прекрасным примером упорядоченно­сти параметрического множества является время. Переменные с линейно упорядоченными множествами состояний называются переменными с упорядоченной шкалой.

Одним из наиболее существенных свойств является расстояние между парой элементов изучаемого множества. Эта мера определяется функцией, сопоставляющей лю­бой паре элементов этого множества число, определяющее, на ка­ком расстоянии друг от друга находятся эти элементы с точки зрения некоторого фундаментального упорядочения.

 ∆ Для данного множества, скажем множества 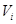, расстояние определяется функцией вида

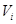
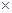
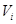 : →R , (1.12)

Однако для того, чтобы эта функция отвечала интуитивному пред­ставлению о расстоянии, она должна удовлетворять следующим условиям для всех х, у, z   :

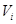(1)  (x, y)  0      (условие неотрицательности);

(2)  (x, y) = 0    тогда и только тогда, когда х = у  (условие нулевого расстояния, называемое также условием невырожденно­сти);

(3)  (x, y) = (y, x)  (симметричность);

(4)  (x, y)  (x, y) +(y, z)   (неравенство треугольника).

Любая функция, удовлетворяющая условиям (1) - (4), называется метрическим расстоянием на множестве 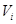, а пара (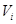, )  — метрическим пространством. Метрическое расстояние можно, ра­зумеется, определить как на множестве состояний, так и на пара­метрическом множестве. ▲

Примерами переменных с выраженными и существенными мет­рическими расстояниями являются почти все переменные в физи­ке, например длина, масса. Совершенно очевидно, что и пространство, и время — это парамет­ры, к которым вполне естественно применимо понятие метричес­кого расстояния. Однако редко удается определить метрическое расстояние на группах. Одним из таких примеров является группа студентов, линейно упорядоченная по показателям их успеваемо­сти. Переменные, с множеством состояний которых связано метрическое расстояние, обычно называются метрически­ми переменными.

Еще одним свойством множеств состояний и параметрических множеств, имеющим большое значение как методологическое от­личие, является непрерывность. Это понятие хорошо известно из математического анализа, и нет необходимости рассматривать его здесь подробно.

Наилучшим примером непрерывного частичного упорядочения является отношение «меньше или равно», определенное на множе­стве действительных чисел или на его декартовых произведениях. Фактически само понятие непрерывной переменной (или непре­рывного параметра) опирается на требование, чтобы соответству­ющее множество состояний (или параметрическое множество) бы­ло изоморфно множеству действительных чисел.

Из этого следует, что множество состояний любой непрерыв­ной переменной или параметрическое множество любого парамет­ра бесконечно и несчетно. Тем самым альтернативой непрерывным переменным и параметрам являются переменные и параметры, за­данные на конечных множествах или, возможно, на бесконечных счетных множествах. Последние называются дискретными пере­менными или параметрами.

1.10 Методологические отличия на уровне переменных и па­раметров

Для нас такие свойства, как упорядоченность, метрическое рас­стояние и непрерывность множеств состояний и параметрических множеств, представляют основу для определения наиболее суще­ственных методологических отличий на уровне переменных и па­раметров. Приведем список перенумерованных альтернатив для этих свойств:

                                                              0 — упорядоченности нет

  Упорядоченность:                            1  — частичная упорядоченность

                                                              2 — линейная упорядоченность

  Расстояние:                                       0 — не определено

                                                              1 — определено

  Непрерывность:                                0 — дискретно

                                                              1 — непрерывно

Статус любой переменной (или параметра) для этих трех свойств может быть однозначно охарактеризован триплетом

(упорядоченность, расстояние, непрерывность),

в котором каждое свойство представляется его определенным зна­чением (или его идентификатором). Так, например, триплет (2, 1, 0) описывает дискретную переменную с линейно упорядоченным множеством состояний, на котором определено метрическое рас­стояние.

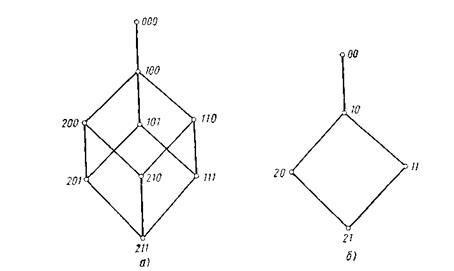
Рис. 1.2. Решетки методологических типов переменных или параметров

Хотя данные три свойства в принципе определяют 12 возмож­ных комбинаций, три из них (0, 0, 1), (0, 1, 0) и (0, 1, 1) смысла не имеют. В самом деле, если на множестве не определена упоря­доченность, то на нем нельзя ни содержательно определить метри­ческое расстояние, ни рассматривать его как непрерывное. Таким образом, имеется девять осмысленных комбинаций. Будем назы­вать эти комбинации методологическими типами переменных и па­раметров.

Они могут быть частично упорядочены с помощью от­ношения «быть методологически более определенным чем». На рис. 1.2,а это частичное упорядочение, образующее решетку,

пред­ставлено в виде диаграммы Хассе. Упрощенная решетка на рис. 1.2,б задает схему для свойств упорядоченности и расстояния, но без непрерывности.

        Теперь предположим, что имеется m параметров. Они могут быть одного, двух, трех (неза­висимо от порядка) и т.д. ти­пов. Предположим, что  (это довольно разумное пред­положение), тогда общее чис­ло методологических типов полного параметра определяется суммой

 ,(1.13)

Вам также может быть полезна лекция "Сети. Модель OSI".

При сочетании этой суммы с девятью методологическими типами переменных мы полу­чим общее число возможных методологических отличий одной переменной и ее параметра, это число определяется формулой

.(1.14)

Алгоритм формализации систем объекта

1. Определяются свойства a_i и мно­жества их проявлений A_i .
2. Определяются базы b_j и множества их проявлений B_j .
3. Определяется система объекта , где N_n={1, 2, …, n}, a N_m={1, 2, …, m}.

К.Р. № 5               

            Опишите две системы с различными методологическими отличиями.