Каналы наблюдения

Лекция 4

1.7 Каналы наблюдения

            Назовем каналом наблюдения понимаем любую операцию, вводящую конкретную переменную как отображение (или конкретизацию) свойства.

 Канал наблюдения, с помощью которого свойство a_i представляется переменной , реализуется функцией

O_i : A_i→ , (1.6)

Эта функция гомоморфна относительно предполагаемых свойстви множеств A_i и.

Аналогичная функция, скажем

ω_j : B_j → , (1.7)

Рекомендуемые материалы

задает представление базы b_j, параметром , она также должна быть гомоморфной относительно соответствующих свойств базы (например, времени) и множества ▲

Для некоторых свойств и баз каналы наблюдения могут пред­ставлять собой явно заданные функции o_i и ω_j Однако в других случаях, когда множества А и В неизвестны. При этом представления свойств и баз вводятся физически (операционно), а не с помощью математических определений.

За исключением тривиальных случаев, когда функции o_i и ω_j, определены ясно, канал наблюдения представляет собой физиче­ское устройство и процедуру, описывающую его применение. Это устройство обычно называется измерительным прибором или ин­струментом. Процедура представляет собой набор команд, опреде­ляющих то, как следует использовать инструмент в разных усло­виях.

Любой измерительный инструмент должен уметь взаимодействовать с измеряемым свойством и пре­образовывать это взаимодействие в вид, непосредственно представляющий состояния соответствующей переменной (например, показания указателя на шкале буквенно-цифрового дисплея или просто запись значений).

Несмотря на то, что измерительные инструменты и процедуры, образующие каналы наблюдения, должны соответствовать некото­рым общим принципам измерения, они существенно зависят от того, что они измеряют. Поэтому их изучением, созданием и ис­пользованием занимаются, главным образом, в рамках традици­онных научных дисциплин.

Каналы наблюдения учитываются в схеме АСНИ только как компоненты, необходимые для полного определения любой ре­ально существующей системы. В АСНИ они достаточно часто не вклю­чаются.

Пример 1.1. Для иллюстрации введенных понятий положим, что a_i — это установленный ежегодный доход налогоплательщика некоторой страны за последний год, как сообщается в его налоговой деклара­ции за этот год. Тогда A_i — это всевозможные суммы денег от нуля до максимально представимой суммы, ска­жем до 100000.00 единиц. Это множество конечно, так как минималь­ная имеющая хождение денежная величина — 0.1 единицы. Мы понимаем также, что это множество полностью (линейно) упорядочено. Для вычисления подоходного налога достаточно рассматривать только диапазоны облагаемого налогом дохода, где каждому диапазону соответствует определенный процент дохода, который следует вы­платить в качестве подоходного налога. Для упрощения будем этими диапазонами считать диапазоны 0—4999.99, 5000.00 — 9999.99, .... 90000.00 —94999.99, 95000.00—100000.00 и пусть множеством состояний , конкретной переменной , представля­ющей свойство a_i , будет множество минимальных значений этих диапазонов. Содержательное представление a_i с помощью  мож­но ввести с помощью функции о_i, которая для каждого диапазона любому значению из диапазона присваивает минимальное значе­ние в этом диапазоне, например о_i (52357) =50 000 или о_i (796) =0. Очевидно, что функция  о_i  гомоморфна относительно полного упорядочения A_i, так как для любой пары

α, β  A_i,  если α  β,  о_i(α,)  о_i (β) . Из методических соображений обобщенная перемен­ная v_i может быть для конкретной переменной  определена с по­мощью абстрагирующей функции e^-1_i : → V_i . Эта функция долж­на быть изоморфной относительно упорядочения на . Предполо­жим, что нужно, чтобы множество V_i представляло собой набор значений целых чисел. Тогда e^-1_i  можно, вероятно, наиболее есте­ственным образом, задать следующим уравнением:

                                               e^-1_i   (5000k)=k  (k=0,1,…, 19)                                                

Базой в этом примере является множество нало­гоплательщиков определенной категории, скажем множество жи­телей города Х. Данное множество не обладает никакими математическими свойствами. Таким образом,  ω_j : B_j →   может быть любой взаимно однозначной функцией, которая каждому на­логоплательщику ставит в соответствие уникальный идентифика­тор. Методологически удобно абстрагирование ε^-1_j:→W_j  представить в виде взаимно однознач­ной функции, ставящей в соответствие целым числам

из множест­ва N_n, где n — число налогоплательщиков в этой группе.

1.8 Нечеткие каналы наблюдения

Остановимся более подробно на понятии канала наблюде­ния. До сих пор мы его определяли через функции о_i и ω_j , опре­деленные соответственно в уравнениях (1.6) и (1.7). Эти функции предполагают разбиения множеств A_i и B_j на некоторые подмножества,  обозначим их соответственно  A_i/о_i и B_j/ω_j. Элементы любого подмножества в этом разбиении эквивалентны в том смысле, что они не различаются с точки зрения введенной процедуры наблюдения. В таком разбиении каждое подмножество целиком представляет одно состояние переменной  или одно значение параметра . Когда наблюдение свойства a_i, проводится при не­котором значении параметра, то наблюдаемое свойство получает определенное проявление (значение) из множества A_i. Это про­явление является элементом одного и только одного подмножества A_i/о_i. Функция о_i  присваивает его определенному состоянию переменной . Таким образом, предполагается, что любое наблю­дение позволяет нам определить, к какому подмножеству A_i/о_i принад­лежит данное проявление, даже если отдельное проявление и нельзя идентифицировать.

Предположение о том, что различие подмножеств A_i/о_i может быть обнаружено по результатам наблюдений, оправдывается только в том случае, когда ошибки наблюдения исключены. Подобные случаи, как показано в примере 1.1, встречаются, но относительно нечасто. При этом подмножество A_i/о_i правильно определяется во всех случаях, кроме тех, когда фактическое проявление оказывается близко от границы между подмножествами, т. е. в пределах ожидаемой ошибки наблюдения.

Поскольку свойства (по крайней мере некоторые из них) не кон­тролируются исследователем, невозможно предотвратить прояв­ления свойств в нежелательной близости от границ между подмножествами A_i/о_i и, следовательно, можно только сократить возможность определения неправильных подмножеств по наблюдениям благодаря правильному выбору канала наблюдения о_i . Исключить такую воз­можность полностью нельзя.

В результате появления возможности ошибок измерения с про­явлениями возле границ между подмножествами A/о_i связана опреде­ленная недостоверность наблюдения. Имеется два варианта интер­претации этой недостоверности. Здесь мы рассмотрим, и будем придерживаться одного из них.

Разбиение множества A_i задается функцией о_i. Это то же самое разбиение A_i/о_i , что рассматривалось выше. Достоверно  неиз­вестно, к какому подмножеству A_i/о_i принадлежит заданный элемент A_i..  Эта недостоверность может быть задана функцией, сопоставляю­щей любой паре  (элемент A_i, подмножество A_i /о_i)  число  (обычно между 0 и 1 – некий аналог вероятности).

Определенное таким образом число в заданном контексте выражает степень достоверности того, что данный элемент при­надлежит данному подмножеству.

Иными словами все выше сказанное обозначает, что, делая какое-то наблюдение, мы можем утверждать, что мы наблюдали, именно такие факты, лишь с некоторой вероятностью.

Формально вышеупомянутая функция достоверности наблюдений может быть записана следующим образом

 : A_i A_i /о_i → [0, 1], (1.8)

Однако, поскольку каждое подмножество A_i/о_i однозначно представляется  (помечается) состоянием из множества  (в соответствии с функцией о_i), функциюможно задать в более удобном виде

 : A_i  → [0, 1], (1.9)

Определенная в уравнении (1.9) функцияхарактеризует на­блюдения свойства a_i в смысле их недостоверности. В этом смысле  можно назвать нечетким каналом на­блюдения. Во избежание недоразумений о_i будем называть чет­ким каналом наблюдения. ▲

Ясно, что для определения нечеткого канала наблюдения необ­ходимо сначала задать четкий канал наблюдения о_i. Четкий ка­нал наблюдения можно также рассматривать как частный случай нечеткого. В самом деле, если

то задает четкую функцию из A_i в , идентичную о_i .

При рассмотрении баз можно ввести функцию

 : B_j    → [0, 1], (1.10)

подобную функции (1.9) и основанную на соотношении (1.7). Здесь (x, y) — степень достоверности того, что х принадлежит подмножеству B_j/ω_j, который представлен значением у параметра . На практике, однако, эта функция не используется.

Для любых практических на­добностей достаточно использовать четкий канал наблюдения ω_j  для баз, будь то группа, время или пространство. Однако для свойств применимы как четкие, так и нечеткие каналы наблюде­ния (о_i и  ), и  при разных обстоятельствах более подходящим может быть тот или иной тип канала.

Пример 1.2. Пусть свойством a_i является возраст человека из группы B_j. И пусть элементами A_i будут номера лет в диапазоне от 0 до 100. Положим, что . = {очень молодой, молодой, средних лет, старый, очень старый}, и пусть о_i — это взаимно однозначная функция A_i /о_i → , определенная следующим

образом:

{0, 1, …, 14}        - очень молодой,

{15, 16, …, 29}    - молодой,

{30, 31, …, 49}    - средних лет,

{50, 51, …, 74}    - старый,

{75, 76, …, 100}  - очень старый.

При использовании четкого канала наблюдения очень плохо описываются люди, чей возраст близок к границам между бло­ками A_i /о_i. Например, 49-летний человек помечается как человек средних лет, а 50-летний, как старый. При использовании нечет­кого канала о_i, например такого, какой описан на рис. 1.1, приве­ден оказывается более подходящим, поскольку не дает таких рез­ких скачков. Важно отметить, что нечеткий канал наблюдения да­ет не одно состояние  для одного наблюдения, как четкий канал, а набор значений  для всех . Так, например, при наблюдении 25-летнего человека через нечеткий канал будут полу­чены следующие 5 значений:

(25, очень молодой) = 0.1

(25, молодой) = 0.97

(25, старый) = 0

Вам также может быть полезна лекция "Лекция 10".

(25, очень старый) = 0.

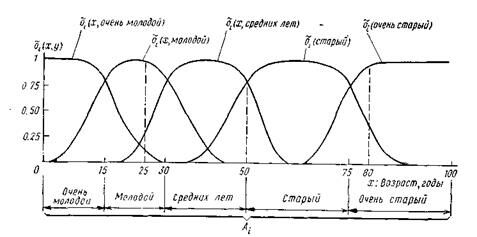
Рис. 1.1. Четкий и нечеткий каналы наблюдения для полностью упорядоченного признака «возраст человека»

К.Р. № 4

Приведите пример систем с четкими и нечеткими каналами наблюдения, формализуйте их.