Виды порождающих систем
Лекция 17
4.18 Виды порождающих систем
системы с поведением
1. базовые-
a. уравнение (4.12)—нейтральные;
b. уравнение (4.28)—направленные;
2. порождающие:
a. уравнение (4.19)—нейтральные;
Рекомендуемые материалы
b. уравнение (4.32)—направленные;
ST-системы
1. базовые:
a. уравнение (4.66) —нейтральные,
b. уравнение (3.93)—направленные;
2. порождающие:
a. уравнение (4.86) — нейтральные;
b. уравнение (4.87)—направленные.
Как было показано, любая ST-система может быть преобразована в изоморфную систему с поведением, в то время как обратное преобразование возможно только при определенном типе масок. Следовательно, системы с поведением более общие, чем ST-системы.
Два основных недостатка ST-систем очевидны: ограниченность из-за использования только компактных масок и собственная избыточность, проистекающая из наложения текущего и следующего состояний.
ST-системы, когда они применимы, представляют для исследователей определенные преимущества. По-видимому, ST-функции понятнее человеку, чем аналогичные функции поведения.
Для порождающих систем выделены различные отличия. Это отличия, выделенные для систем более низких уровней, и некоторые новые. Среди первых наиболее существенными являются:
1. упорядоченность параметрического множества, что позволяет ввести важное понятие маски;
2. упорядоченность множеств состояний, что играет существенную роль в упрощении процедур для порождающих систем и при работе с не полностью определенными наборами данных;
3. отличие четких и нечетких каналов наблюдения, дающих соответственно четкие или нечеткие данные и требующих применения различных методов обработки данных;
4. отличие между нейтральными и направленными системами, с которыми следует обращаться по-разному.
Отличиями, относящимися к порождающим системам, но не к системам данных и исходным системам, являются:
1. детерминированность и недетерминированность систем;
2. по используемой маске различаются порождающие системы без памяти и системы, зависящие от прошлого.
Разумеется, эти методологические отличия характеризуют и системы более высоких уровней.
4.19 Упрощение порождающих систем
На некотором этапе обработки заданной системы данных часто желательно бывает упростить соответствующие этой системе данных порождающие системы.
Существует два основных метода одновременного упрощения систем данных и соответствующих порождающих систем:
1) упрощение за счет исключения некоторых переменных из соответствующей подобной системы;
2) упрощение за счет определения классов эквивалентности состояний некоторых переменных.
 Пусть множество переменных порождающей системы V состоит из п переменных и любое подмножество V, за исключением пустого множества, представляет содержательное упрощение первого рода. Следовательно, имеется
Пусть множество переменных порождающей системы V состоит из п переменных и любое подмножество V, за исключением пустого множества, представляет содержательное упрощение первого рода. Следовательно, имеется  нетривиальных упрощения первого рода. Они частично упорядочены по отношению «подмножество». Если для удобства включить исходное множество V и пустое множество, то множество упрощений с частичным упорядочением образует решетку. Назовем эту решетку решеткой переменных или V-решеткой и обозначим
нетривиальных упрощения первого рода. Они частично упорядочены по отношению «подмножество». Если для удобства включить исходное множество V и пустое множество, то множество упрощений с частичным упорядочением образует решетку. Назовем эту решетку решеткой переменных или V-решеткой и обозначим  . Понятно, что V -решетка может быть описана или как
. Понятно, что V -решетка может быть описана или как
или как  (4.88)
(4.88)
Обозначим через fB функцию поведения заданной системы с поведением с переменными, составляющими множество V. При упрощении этой системы с помощью сокращения множества V до подмножества  новая (упрощенная) функция поведения fB определяется проекцией
новая (упрощенная) функция поведения fB определяется проекцией
 ,(4.89)
,(4.89)
определенной уравнением (4.57).
Сокращения второго рода сводятся к уменьшению числа состояний, выделяемых для отдельных переменных. Одним из способов их описания является определение функции
 (4.90)
(4.90)
где  — заданное множество состояний (переменной
— заданное множество состояний (переменной  );
);  — упрощенное (сокращенное) множество состояний той же переменной;
— упрощенное (сокращенное) множество состояний той же переменной;  — новое состояние, присвоенное исходному состоянию
— новое состояние, присвоенное исходному состоянию  , а
, а  — это идентификаторы, с помощью которых различаются разные функции вида (4.90), примененные к множеству состояний одной и той же переменной. Если
— это идентификаторы, с помощью которых различаются разные функции вида (4.90), примененные к множеству состояний одной и той же переменной. Если  , то состояния х и у из
, то состояния х и у из при упрощении оказываются неразличимыми. Функция (4.90) должна быть голоморфна относительно всех математических свойств исходного множества Vi , которые считаются существенными с точки зрения рассматриваемой задачи. Будем функцию (4.90), являющуюся гомоморфизмом в описанном выше смысле, называть упрощающей функцией.
при упрощении оказываются неразличимыми. Функция (4.90) должна быть голоморфна относительно всех математических свойств исходного множества Vi , которые считаются существенными с точки зрения рассматриваемой задачи. Будем функцию (4.90), являющуюся гомоморфизмом в описанном выше смысле, называть упрощающей функцией.
Любая упрощающая функция индуцирует разбиение на множестве . Любое разбиение
. Любое разбиение  состоит из групп состояний V,, которые неотличимы при данном упрощении. Будем такое разбиение (которое сохраняет существенные свойства
состоит из групп состояний V,, которые неотличимы при данном упрощении. Будем такое разбиение (которое сохраняет существенные свойства  ) называть разрешающей формой.
) называть разрешающей формой.
Разрешающие формы, определенные на каком-то множестве состояний  , могут быть упорядочены с помощью обычного отношения уточнения, определенного на разбиениях данного множества. Хорошо известно, что такое отношение уточнения является отношением частичного порядка и образует решетку. Для двух заданных разбиений, скажем X и У, определенных на одном и том же множестве, будем говорить, что X является уточненным разбиением Y тогда и только тогда, когда для любой группы х из X существует группа у из У, такая, что
, могут быть упорядочены с помощью обычного отношения уточнения, определенного на разбиениях данного множества. Хорошо известно, что такое отношение уточнения является отношением частичного порядка и образует решетку. Для двух заданных разбиений, скажем X и У, определенных на одном и том же множестве, будем говорить, что X является уточненным разбиением Y тогда и только тогда, когда для любой группы х из X существует группа у из У, такая, что  . Если X, уточняющее разбиение У, то У называется укрупненным разбиением X. Решетку разрешающих форм, определенных на множестве состояний
. Если X, уточняющее разбиение У, то У называется укрупненным разбиением X. Решетку разрешающих форм, определенных на множестве состояний  , будем называть разрешающей решеткой и обозначать
, будем называть разрешающей решеткой и обозначать  . Любая разрешающая решетка множества состояний
. Любая разрешающая решетка множества состояний  может быть определена или в виде
может быть определена или в виде
 (4.91)
(4.91)
или в виде
 (4.92)
(4.92)
где  и
и  обозначают соответственно произведение и сумму разбиений.
обозначают соответственно произведение и сумму разбиений.
Если рассматриваемое множество состояний не обладает математическими свойствами, которые должны быть сохранены, то в качестве разрешающей формы приемлемо любое разбиение.
В этом случае разрешающая решетка содержит все разбиения, которые могут быть определены на этом множестве состояний. Если множество состояний состоит из m состояний, то число разрешающих форм в решетке, определяется формулой
 (4.93)
(4.93)
Ниже показано огромное число разрешающих форм даже для небольшого числа состояний:

Поскольку наименьшая уточненная разрешающая форма (все состояния в одном блоке) смысла не имеет, а наибольшее уточнение дает упрощения, то число осмысленных упрощений равно .
.
Если множество состояний полностью упорядочено и требуется сохранить эту упорядоченность при упрощениях, то число разрешающих форм существенно меньше числа, задаваемого формулой. Пусть  — это состояния и
— это состояния и  . Тогда для любого
. Тогда для любого  и
и  или объединяются в одну группу или нет. Только эти решения определяют конкретное разбиение. Таким образом, для т состояний принимается m—1 бинарное решение. Следовательно, для полностью упорядоченных множеств состояний
или объединяются в одну группу или нет. Только эти решения определяют конкретное разбиение. Таким образом, для т состояний принимается m—1 бинарное решение. Следовательно, для полностью упорядоченных множеств состояний
 (4.94)
(4.94)
Очевидно, что эта решетка для m состояний изоморфна булевской решетке для упорядочения подмножеств любого множества из m—1 элемента. В следующей таблице приводятся значения  , вычисленные по формуле (3.94); в этом случае число разрешающих форм существенно меньше, чем в случае неупорядоченных множеств состояний:
, вычисленные по формуле (3.94); в этом случае число разрешающих форм существенно меньше, чем в случае неупорядоченных множеств состояний:

Число содержательных упрощений снова равно
Пример 4.7. Рассмотрим переменную, состояниями которой являются цвета светофора: красный, желтый, зеленый. Поскольку они не упорядочены, все разбиения множества состояний приемлемы в качестве разрешающих форм. Диаграмма Хассе для этой решетки приведена на рис. 4.13. Буквы к, ж, з означают соответственно красный, желтый и зеленый цвета. Группам в отдельных разрешающих формах показаны черточками над соответствующими буквами. Стрелка на диаграмме указывают направление уточнения разбиений. Для упрощения исходной системы нужно двигаться в направлении, обратном стрелкам.
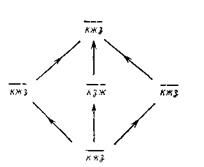
Рис. 4.13. Решетки разрешающих форм.
Если выбрано несколько переменных, то любая разрешающая форма для одной переменной может быть объединена с любой разрешающей формой другой переменной. Все эти комбинации можно включить в одну решетку, представляющую выбранный набор переменных. Будем называть ее объединенной разрешающей решеткой. Математически она представляет собой произведение отдельных разрешающих решеток.
 Пусть
Пусть — множества элементов отдельных разрешающих решеток выбранных переменных, а X — множество элементов соответствующей разрешающей решетки. Понятно, что общее число элементов объединенной разрешающей решетки равно произведению числа элементов отдельных разрешающих решеток, т. е.
— множества элементов отдельных разрешающих решеток выбранных переменных, а X — множество элементов соответствующей разрешающей решетки. Понятно, что общее число элементов объединенной разрешающей решетки равно произведению числа элементов отдельных разрешающих решеток, т. е.
 (4.95)
(4.95)
однако только некоторые из них являются содержательными упрощениями. В частности, любая комбинация, в которую входит наименьшая уточненная разрешающая форма (разбиение на одну группу) одной из разрешающих решеток, является бессмысленной. Комбинация всех наиболее уточненных разрешающих форм также не представляет упрощения. Следовательно, общее число элементов объединенной решетки, представляющих содержательные упрощения,  определяется по формуле
определяется по формуле
 (4.96)
(4.96)
В частном случае, когда все отдельные решетки одинаковы и каждая состоит из  разрешающих форм, мы получаем
разрешающих форм, мы получаем
 (4.97)
(4.97)
Более того, если все разрешающие решетки построены на полностью упорядоченном множестве с т состояниями, то
 (4.98)
(4.98)
Требования, упрощающие порождающие системы:
1) чтобы системы были как можно проще;
2) чтобы степень порождающей нечеткости систем была как можно меньше.
Будем называть требование 1 требованием простоты, а требование 2 требованием четкости.
Чтобы конкретизировать требование простоты для систем с поведением следует задать определенную меру сложности. Пусть, например, сложность системы с поведением оценивается числом реальных состояний системы, т. е. числом состояний, имеющих ненулевые вероятности или возможности. Это очень простая мера, но, возможно, наиболее содержательная.
Алгоритмы формализации порождающих систем
Системы с поведением
- Определяется правило сдвига
![]() (Если параметрическое множество полностью упорядочено
(Если параметрическое множество полностью упорядочено ![]() ).
). - Определяются выборочные переменные
![]() , где
, где ![]() .
. ![]() обозначает состояние выборочной переменной
обозначает состояние выборочной переменной ![]() при значении параметра w, а
при значении параметра w, а ![]() — состояние переменной
— состояние переменной ![]() при значении параметра
при значении параметра ![]() .
. - Определяется маска
![]() . Для введения выборочных переменных определяется функция
. Для введения выборочных переменных определяется функция ![]() .
. - Определяется функция поведения
![]() , где
, где ![]() .
. ![]() , если состояние с имеет место быть, и
, если состояние с имеет место быть, и ![]() в противном случае.
в противном случае. - Определяется система с поведением
![]() .
.
Порождающие системы с поведением
- Определяются подмаски
![]() и
и ![]() маски М. Порождаемая подмаска
маски М. Порождаемая подмаска ![]() и порождающая подмаска
и порождающая подмаска ![]() .
. ![]() - маска порождения.
- маска порождения. - Для удобства определяются функции
![]()
![]() . Множества состояний
. Множества состояний ![]() и
и ![]() соответственно порождаемых и порождающих переменных
соответственно порождаемых и порождающих переменных ![]()
![]()
- Определяется порождающая функция поведения
![]() .
. - Определяется порождающая система с поведением
![]() .
.
Для недетерминированных систем с поведением
Функция поведения принимает вид  закона распределения вероятностей. В случае порождающих систем с поведением
закона распределения вероятностей. В случае порождающих систем с поведением  .
.
Направленные системы с поведением
- Определяются подмаски
![]() и
и ![]() маски М. Пусть подмаска
маски М. Пусть подмаска ![]() определяет выборочные переменные, задаваемые средой, а подмаска
определяет выборочные переменные, задаваемые средой, а подмаска ![]() — остальные.
— остальные. ![]() - маска направленной системы с поведением.
- маска направленной системы с поведением. - Для удобства определяются функции
![]()
![]() . Также
. Также ![]()
![]() .
. - Определяется функция поведения
![]() .
. - Определяется направленная система с поведением
![]() .
.
Информация в лекции "25 - Обмен энергии и терморегуляция" поможет Вам.
Направленные порождающие системы с поведением
- Порождающая маска для направленной системы с поведением
![]() .
. ![]() рассматривается как разбиение
рассматривается как разбиение ![]() .
. - Определяется функция поведения
![]() .
. - Определяется направленная порождающая система с поведением
![]() .
.
Системы с изменяющимися состояниями
1. Определяются функции где
где  — это вероятность состояния
— это вероятность состояния  , следующего непосредственно за состоянием
, следующего непосредственно за состоянием  (согласно выбранному порядку порождения);
(согласно выбранному порядку порождения);  где
где  — условная вероятность того, что при текущем состоянии
— условная вероятность того, что при текущем состоянии  следующим состоянием будет состояние
следующим состоянием будет состояние .
.
2. Определяются аналоги нейтральных систем с поведением, ST-система  , и порождающая ST-система
, и порождающая ST-система  . Где
. Где  ,
,  и
и  имеют тот же смысл, что в системах с поведением.
имеют тот же смысл, что в системах с поведением.
К.Р. № 17
Для некоторой порождающей системы приведите примеры возможных упрощений.



 (Если параметрическое множество полностью упорядочено
(Если параметрическое множество полностью упорядочено  ).
). , где
, где  .
.  обозначает состояние выборочной переменной
обозначает состояние выборочной переменной  при значении параметра w, а
при значении параметра w, а  — состояние переменной
— состояние переменной  при значении параметра
при значении параметра  .
.  . Для введения выборочных переменных определяется функция
. Для введения выборочных переменных определяется функция  .
. , где
, где  .
.  , если состояние с имеет место быть, и
, если состояние с имеет место быть, и  в противном случае.
в противном случае. .
. и
и  маски М. Порождаемая подмаска
маски М. Порождаемая подмаска  - маска порождения.
- маска порождения.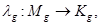
 . Множества состояний
. Множества состояний  и
и  соответственно порождаемых и порождающих переменных
соответственно порождаемых и порождающих переменных 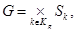
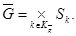
 .
. .
. и
и  маски М. Пусть подмаска
маски М. Пусть подмаска  - маска направленной системы с поведением.
- маска направленной системы с поведением.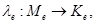
 . Также
. Также 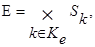
 .
.  .
. .
. .
.  рассматривается как разбиение
рассматривается как разбиение  .
. .
.
















