Взаимосвязь ST-систем

Лекция 16

4.17 Взаимосвязь ST-систем и систем с поведением

Любую ST-систему легко можно преобразовать в изоморфную систему с поведением. Чтобы показать, как это делается, возь­мем произвольную ST-систему

(4.76)

где М, разумеется, компактная маска. Предположим, что любое следующее состояние соответствует большему значению пара­метра, чем предшествующее.

Рассмотрим теперь систему с поведением

(4.77)

гдеопределяется через М следующим образом:

Рекомендуемые материалы

 (4.78)

Тогда для любого набора данных из общей представляющей системы I все выборки данных, дающие одну пару состояний для маски М, скажем пару, дают и одно и то же состояние для маски, скажем состояние с+. Если данные полностью выби­раются с помощью обеих масок, то частоты и должны быть одинаковы. Следовательно,

,(4.79)

где состояние состоит из с и порождаемой части, назовем ее. Таким образом, функция поведения эквивалентна ST-функции при однозначном соответствии

(4.80)

где тогда и только тогда, когда .

Маску  (4.78)   будем    называть    расширенной маской М. Она определена в предположении, что состояния порождаются в порядке возрастания параметра. При обратном порядке аль­тернативная расширенная маска, скажем маска , определя­ется несколько иначе:

(4.79)

Можно аналогично тому, как это было показано для М+, по­казать, что система с поведением

,(4.80)

изоморфна ST-системе, определенной для той же представляющей системы I и маски М.

Соответствие между масками М,и масками М,пока­зано соответственно на рис. 4.11а и б. На рисунке также показано однозначное соответствие и его аналог для маски  и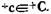

Для заданной системы с поведением

(4.81)

Изоморфная ST-система  при той же представляющей системе I существует только тогда, когда М — компактная маска и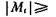 для любой подмаски . Если эти условия выполнены, то по­нятно, что ST-система(4.82)

где - порождаемая часть (согласно определенному порядку по­рождения), которая изоморфна при соответствующем однозначном соответствии между множествами состояний С (основанном на М) и  (основанном на ). Данное преобразование из системы с поведением в изоморфную ST-систему для одного из порядков порождения показано на рис. 4.11,в.

Для направленных систем изменяющими состояние аналогами функций поведения  будут соответственно следующие ST-функции:

 (4.83)

где Е имеет тот же смысл, что   и   для   систем   с   поведением,   и   — условная вероятность, смысл ко­торой однозначно определяется ее общепринятым обозначением

 (4.84)

где — порождающие условные вероятности;

(4.85)

где.

Изменяющими состояния аналогами для направленных систем с поведением будут соответственно направленная ST-система

 (4.86)

 и направленная порождающая ST-система

 (4.87)

где  и определяются так же, как и для систем с поведением.

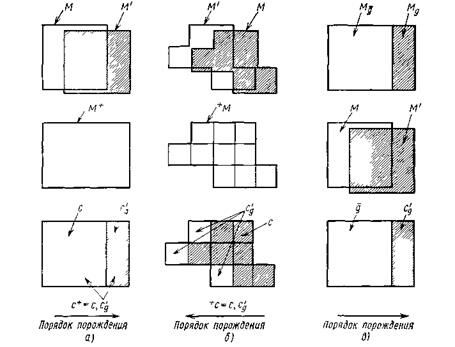
Рис. 4.11. Изоморфизм между системами с поведением и ST-системами

Бесплатная лекция: "3 - Проектирование АИС" также доступна.

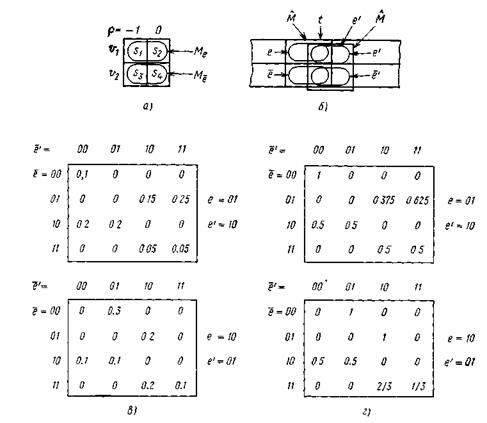
Рис. 4.12. Трехмерный массив, представляющий направленную ST-систему

Функции (4.83) и (4.84) удобно представлять в виде массивов квадратных матриц (трехмерных массивов) по одной матрице для каждого условия . Удобны также диаграммы, подобные диа­граммам для нейтральных ST-систем. Для направленных систем связи на диаграммах помечаются не только значениями соответ­ствующей ST-функции, но и условиями . Функции (4.85) мож­но представлять в виде матриц, строки которых соответствуют со­стояниям е, столбцы — состояниям , а элементами являются со­ответствующие состояния . Эти функции представляются также в виде диаграмм, таблиц и в некоторых случаях с помощью алге­браических формул. ▲

Пример 4.6. На рис. 4.12 приведена простая направленная ST-система (без интерпретации). Ее представляющая система со­стоит из входной переменной  и выходной переменной , каждая имеет два состояния 0 и 1. Маска системы М показана на рис. 4.12,а, а на рис. 4.12,б приведены соответствующие компоненты состояний, порожденные двумя ее последовательными положени­ями на матрице данных. На рис. 4.12,в и г показаны соответствен­но функции и в виде трехмерных массивов. В данном при­мере массив состоит из двух матриц.

К.Р. № 16

Приведите пример перехода от некоторой ST-системы к изоморфоной системе с поведением.