Системы с изменяющимися состояниями

                Лекция 15

4.16 Системы с изменяющимися состояниями

Предположим, что снова задана система данных с полностью упорядоченным параметрическим множеством. Как было пока­зано, система данных может быть описана параметрически инвариантно через множество подходящих си­стем с поведением, согласующихся с системой данных и удовлет­воряющих выдвинутым требованиям. Несмотря на то, что системы с поведением совершенно адекватно описы­вают полное ограничение на исследуемые выборочные перемен­ные, существует и другая форма представления этого ограниче­ния, часто представляющаяся конечному исследователю более подходящей. Эта форма обычно называется отношением изменения состояния или сокращенно ST-отношением. Это отношение определяется не на отдельных состояниях, а на после­довательных парах состояний; порождающие системы, в которых используется эта формула представления состояний, называются системами с изменяющимися состояниями или ST-системами.

 Для ST-систем маски выборочные переменные, множества со­стояний выборочных переменных и их декартово произведение С определяются точно так же, как и для систем с поведением, за исключением двух отличий

(1) к ST-системам неприменимо раз­деление выборочных переменных на порождаемые и порождаю­щие, и

(2) содержательные маски в ST-системах имеют дополни­тельные ограничения. Аналогами функций поведения в ST-системах являются функции изменения состояния (или ST-функции). Для нейтральных систем они опре­делены на , а не на С, а для направленных систем на  , а не на .

Для нейтральных систем аналогами функций поведения оп­ределяем формулами (4.11), (4.20), (4.17), являются следующие ST-функции:

(4.63)

Рекомендуемые материалы

где —это вероятность состояния , следующего непосредственно за со­стоянием с (согласно выбранному порядку порождения);

, (4.64)

где —условная вероятность того, что при текущем состоянии с следующим состоянием будет состояние ;    будем    поэтому    использовать    общепринятую    запись :                     

  (4.65)

где, т. е. следующее состояние однозначно определяется текущимсостоянием с; функция специального вида (4.65) применима, разумеется, только к детерминированным системам. Будем  называть порождающими ST-функциями.

Аналогами нейтральных систем с поведением являются соответственно ST-система

,  (4.66)

и порождающая ST-система

  (4.67)

где I, M иимеют тот же смысл, что в системах с поведением.

Для заданных системы данных и маски ST-функция f_ST хоро­шо согласующаяся с системой данных и маской, может быть оп­ределена с помощью полной выборки данных аналогично тому, как это делалось для функции поведения f_B. Единственное отли­чие состоит в том, что в результате выборки получаются частоты  пар последовательных состояний, а не частоты N(c) от­дельных состояний.

Пара называется переходом из состояния с в другое состояниесогласно объявленному на параметрическом множестве порядку порождения. Одним из важнейших свойств ST-функций является то, что переходы в некоторое состояние должны находиться в равновесии с переходами из этого состоя­ния. Если используются вероятности, то для любого состояния  имеем

   (4.68)

и, следовательно,

  (4.69)

что и определяет равновесие переходов.

Состояния с, с' могут рассматриваться как состояния, опре­деляемые двумя взаимосвязанными масками М, М'. Маски связаны между собой простым сдвигом в соответствии со следующи­ми правилами сдвига:

 тогда и только тогда, когда,  (4.70)

если данные порождаются в порядке возрастания параметра, или

 тогда и только тогда, когда,  (4.71)

если данные порождаются в обратном порядке.

Маски используются вместе для описания пар состояний.

Чтобы избежать противоречий и неполноты при порождении данных, содержательные маски в ST-системах должны удовлетво­рять следующему требованию (в дополнение к требованиям для масок в системах с поведением):

для заданной маски М, если  ^и  и, то для всех целых, таких, что

Это значит, что маски в ST-системах не должны содержать «пробелы», подобные элементам  на рис. 4.1. Маски, удовлетворяющие этому дополнительному требованию, будем называть компактными масками.

Для обоснования этого требования предположим, что маска М ST-системы некомпактна. Тогда существует по крайней мере одна пара элементов из маски М, скажем пара , , такая, что,

 (4.72)

идля всех. Из (4.70) имеем

 (4.73)

Обозначим выборочные переменные, базирующиеся на этих элементах , через  и . Состояния , являются компонен­тами . Тем самым они должны быть или определены для каж­дого значения параметра по состоянию с, или порождаться в со­ответствии с распределением вероятностей или возможностей  для каждого конкретного с. Однако ни один из этих вариантов для  невозможен. Из-за (4.72) оно не может быть определено по состоянию с, не может быть и корректно порожде­но при любом значении параметра t, так как

 >,(4.74)

и, таким образом,  определяется    состоянием s₂ при значении параметра . Нет никакой гарантии, что порожденное состояние  будет соответствовать этому ранее определенному состоянию. С другой стороны, если состояние порождается, то  становится неполным, так как ранее определенное состояние

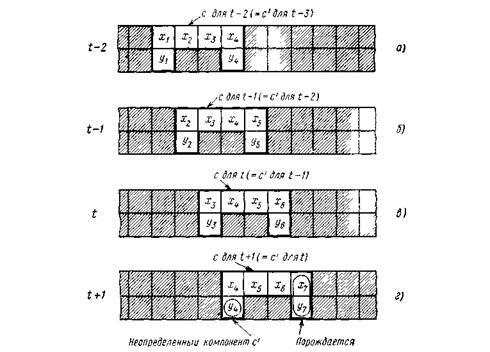
Рис. 4.10. Пример несогласованности или неполноты ST-систем с некомпактными масками

неизвестно (т. е. оно не является компонентом с). Следователь­но, при любом значении t состояние не может быть ни опреде­лено из с, ни порождено с помощью порождающей ST-функции.

Иллюстрацией к доказательству того, что маски с «пробела­ми» недопустимы в ST-системах, служит рис. 4.10; компонент следующего состояния с' при значении параметра t+1 не может быть ни определен из состояния с в момент времени t (рис. 4.10,в), ни порожден с помощью ST-функции, так как уже порожден при значении параметра t—3 (рис. 4.10,а).

Удобно представлять ST-функции (4.63) и (4.64) в виде квад­ратных матриц, строки и столбцы которых связаны соответствен­но с с и. Элементами этих матриц являются значения соответ­ственно или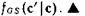

Пример 4.5. Одним из подходов к оценке производительности вычислительной техники является постоянный контроль за ап­паратным обеспечением. Значение этого подхода будет возра­стать по мере возрастания сложности оцениваемых вычислитель­ных систем. При контроле аппаратного обеспечения наблюдаются определенные ключевые переменные, обычно описывающие состояние отдельных компонентов вычислительной системы. Дела­ется это в течение определенного времени обслуживания системы пользователями с помощью так называемых аппаратных мо­ниторов. Данные обрабатываются аппаратным монитором и ана­лизируются с целью обнаружения узких мест в системе и поиска способов повышения производительности, которая также долж­на быть каким-либо образом определена.

Обычно в состав аппаратных мониторов входят счетчики, ко­торые в процессе сбора данных или считают число происшедших событий (режим счета), или измеряют длительность событий (временной режим). Это значит, что обычно аппаратный монитор предоставляет исследователю не фактические данные, а обоб­щенные. Например, монитор определяет, что центральный про­цессор (ЦП) вычислительной системы был загружен в течение 43% времени наблюдения, что канал был занят в 15% всех на­блюдений, но не дает фактической последовательности событий, которые бы можно было затем обрабатывать и анализировать.

При этом часто теряется важная информация, способствую­щая лучшему пониманию вопросов, связанных с производитель­ностью компьютера. Например, совершенно выпадают из анали­за динамические аспекты работы компьютера.

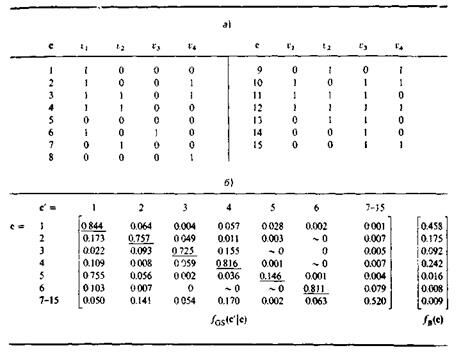
Согласно концепции АСНИ все наблюдения должны быть за­фиксированы, а затем обработаны любым подходящим способом. В данном примере по времени было сделано 409610 наблюдений для четырех переменных v₁, v₂, v₃, v₄. Каждая пере­менная имела два состояния 0 и 1, характеризующие состояние конкретного компонента аппаратного обеспечения: 0 означает, что компонент был неактивен во время наблюдения, а 1 — что активен. Переменная  описывает работу ЦП, а остальные три переменных — работу трех важных каналов связи системы. Для получения вероятностной ST-функции из этого огромного набора данных, превышающего 1,6 млн. бит, с помощью маски без па­мяти была сделана выборка для двух последовательных состоя­ний. Это дало 15 состояний (см. табл. 4.2,а) и 11З переходов. Состояния 7—15 появляются очень редко: вероятность того, что система находится в одном из этих состояний 0.009. Если для уп­рощения ST-функции, объединить эти состояния в одно, что удобно для исследователя, получится матрич­ное представление порождающей ST-функции, приведенное в табл. 4.2,б. Элементами матрицы являются условные вероятно­сти . Обозначение ~0 используется для вероятностей, которыми можно пренебречь; через 0 обозначены переходы, ко­торые вообще не наблюдались. В матрице подчеркнуты элемен­ты, соответствующие переходу из состояния снова в это состоя­ние. В табл. 4.2,б также приведен вектор-столбец значений функции поведения при той же маске (маска без памяти),

Таблица 4.2 ST-функция для исследования по оценке производительности вычислительной системы

Информация в лекции "2.8. Процессы в информационных системах - ИС" поможет Вам.

которая обычно и является результатом контроля работы аппарат­ного обеспечения. Понятно, что

,(4.75)

В некоторых случаях предпочтительнее представлять ST-функ­ции в виде диаграмм. Такая диаграмма представляет собой на­бор узлов, по одному для каждого состояния наблюденных вы­борочных переменных, и ориентированных связей между узлами, соответствующих реально существующим переходам. Узлы на ди­аграмме должны быть помечены соответствующими идентифика­торами состояния с, а связи помечены значениями  или  ; в последнем случае желательно также пометить узлы значениями  так, чтобы значения  можно было вычислить при необходимости из уравнения (4.75).

К.Р. № 15

            Опишите ST-функцию для системы с изменяющимися состояниями.