Функции поведения
Лекция 10
4.4 Функции поведения. Порождающие и порождаемые переменные.
Самый простой способ задания определенной маски — это перечисление всех полных состояний соответствующих выборочных переменных. В общем виде подобный перечень является подмножеством декартова произведения С, т. е. многомерным отношением, определенным на С. Это отношение определяется функцией
 ,(4.11)
,(4.11)
такой, что  , если состояние с входит в перечень, и
, если состояние с входит в перечень, и  в противном случае. Такая функция дает некоторые сведения о поведении выборочных переменных, функцию
в противном случае. Такая функция дает некоторые сведения о поведении выборочных переменных, функцию  обычно называют функцией поведения. Функция, определяемая уравнением (4.11), задает только один из существующих типов функций поведения, разными способами описывающих ограничения на переменные.
обычно называют функцией поведения. Функция, определяемая уравнением (4.11), задает только один из существующих типов функций поведения, разными способами описывающих ограничения на переменные.
Функция  определяет встречающиеся состояния с, но не определяет значение параметра, при котором они имеют место. Таким образом, эта функция является параметрически инвариантной.
определяет встречающиеся состояния с, но не определяет значение параметра, при котором они имеют место. Таким образом, эта функция является параметрически инвариантной.
Система  , характеризующая параметрически инвариантное ограничение на множество переменных через функции поведения, определяется тройкой
, характеризующая параметрически инвариантное ограничение на множество переменных через функции поведения, определяется тройкой
 , (4.12)
, (4.12)
Рекомендуемые материалы
где I — обобщенная представляющая система; М — маска, определенная на I;  —функция поведения, определенная через М и I. Будем такую систему называть системой с поведением
—функция поведения, определенная через М и I. Будем такую систему называть системой с поведением
Несмотря на то, что любая система с поведением, определяемая (4.12), неким конкретным параметрические инвариантно описывает ограничения на переменные представляющей системы, она не содержит описания того, как использовать это ограничение для порождения данных. Для разработки такого описания нужно разбить выборочные переменные на два подмножества:
1) переменные, состояния которых порождаются из ограничения; назовем их порождаемыми переменными;
2) переменные, состояния которых используются как условия в процессе генерации, назовем их порождающими переменными.
Для заданной системы с поведением одним из способов определения порожденных и порождающих переменных является определение для данной маски М двух подмасок  и
и  . Будем
. Будем
 , (4.13)
, (4.13)
где
 ,(4.14)
,(4.14)
называть маской порождения, т. е. это маска М и ее разбиение на порождаемую подмаску  и порождающую подмаску
и порождающую подмаску  .
.
По аналогии с разбиением  на
на  и
и  множество
множество  идентификаторов
идентификаторов  выборочных переменных можно разбить на два подмножества, скажем
выборочных переменных можно разбить на два подмножества, скажем  и
и  , представляющих идентификаторы соответственно порождаемых и порождающих переменных. Для удобства обозначений кодирующая функция (4.7) может быть заменена двумя функциями
, представляющих идентификаторы соответственно порождаемых и порождающих переменных. Для удобства обозначений кодирующая функция (4.7) может быть заменена двумя функциями
 (4.15)
(4.15)
с помощью которых множества состояний  и
и  соответственно порождаемых и порождающих переменных задаются декартовыми произведениями
соответственно порождаемых и порождающих переменных задаются декартовыми произведениями
 (4.16)
(4.16)
Теперь способ представления состояния порождаемых переменных (скажем  ), определяемого по состоянию порождающих переменных (скажем,
), определяемого по состоянию порождающих переменных (скажем,  ), можно выразить функцией
), можно выразить функцией
 , (4.17)
, (4.17)
где
 ,(4.18)
,(4.18)
Назовем эту функцию порождающей функцией поведения.
Если маску М и функцию  из (4.11) заменить соответственно на
из (4.11) заменить соответственно на  и функцию
и функцию  , то получится альтернативная система
, то получится альтернативная система
 . (4.19)
. (4.19)
Будем называть такую систему порождающей системой с поведением.
Использование порождающей системы с поведением для порождения данных включает следующие два этапа:
а) для некоторого значения  задано состояние
задано состояние  ; для определения состояния
; для определения состояния  при том же значении используется функция
при том же значении используется функция  ;
;
б) значение t заменяется на новое и повторяется этап а).
4.5 Особенности процедуры порождения данных
1. На этапе а) неявно предполагается, что при заданном значении t состояние  известно. Это состояние называется начальное условие. Однако после этого все полностью определяется самим процессом порождения, т. е. состояниями
известно. Это состояние называется начальное условие. Однако после этого все полностью определяется самим процессом порождения, т. е. состояниями  и g, связанными с предшествующим значением t. При этом предполагается, что значения t должны на этапе (б) изменяться в соответствии с порядком, заданным на множестве Т. Таким образом, значения t заменяются или на t+l, или на t-1. В первом варианте начальное условие должно быть определено для наименьшего возможного значения t, а во втором — для наибольшего возможного значения t.
и g, связанными с предшествующим значением t. При этом предполагается, что значения t должны на этапе (б) изменяться в соответствии с порядком, заданным на множестве Т. Таким образом, значения t заменяются или на t+l, или на t-1. В первом варианте начальное условие должно быть определено для наименьшего возможного значения t, а во втором — для наибольшего возможного значения t.
2. Из необходимости порождения данных в одном из двух порядков следует, что существует только два содержательных разбиения маски М на  и
и  , каждое из которых соответствует одному из двух порядков порождения. Если данные порождаются в порядке возрастания (убывания) t, то
, каждое из которых соответствует одному из двух порядков порождения. Если данные порождаются в порядке возрастания (убывания) t, то  содержит ровно по одному элементу каждой подмаски
содержит ровно по одному элементу каждой подмаски  , определенной в (4.10), элемент с наибольшим (наименьшим) значением
, определенной в (4.10), элемент с наибольшим (наименьшим) значением  ; остальные элементы М входят в
; остальные элементы М входят в  . Таким образом, графически получается, что
. Таким образом, графически получается, что  — это множество самых правых элементов М (правый край этой маски) или, наоборот, множество самых левых элементов М (левый край маски).
— это множество самых правых элементов М (правый край этой маски) или, наоборот, множество самых левых элементов М (левый край маски).
3. Предполагается, что для любого состояния  имеется по крайней мере одно состояние
имеется по крайней мере одно состояние  , допустимое функцией
, допустимое функцией  [т.е.
[т.е.  ] Если допускается только одно состояние, то для любого начального условия данные порождаются однозначно; такие системы называются детерминированными. Если допускается более чем одно состояние, то порождение данных проблематично, так как порождаемое состояние не всегда однозначно определено. Для таких систем выбирающие функции поведения не подходят. Более содержательно они описываются функциями поведения других типов, рассматриваемых ниже. Для детерминированных систем представление (4.17) порождающей функции поведения
] Если допускается только одно состояние, то для любого начального условия данные порождаются однозначно; такие системы называются детерминированными. Если допускается более чем одно состояние, то порождение данных проблематично, так как порождаемое состояние не всегда однозначно определено. Для таких систем выбирающие функции поведения не подходят. Более содержательно они описываются функциями поведения других типов, рассматриваемых ниже. Для детерминированных систем представление (4.17) порождающей функции поведения  может быть заменено более простым
может быть заменено более простым
 . (4.20)
. (4.20)
Пример 4.1. Для пояснения процесса порождения данных порождающей системой с поведением типа, определяемого уравнением (4.12), положим, что подобная система состоит из упорядоченного параметрического множества  и пяти переменных
и пяти переменных  , состояния которых будут определены ниже. Воспользуемся маской, заданной на рис. 4.2. Данные могут порождаться или в порядке возрастания, или в порядке убывания значений параметра t. Оба эти варианта показаны соответственно на рис. 4.2 и 4.3.
, состояния которых будут определены ниже. Воспользуемся маской, заданной на рис. 4.2. Данные могут порождаться или в порядке возрастания, или в порядке убывания значений параметра t. Оба эти варианта показаны соответственно на рис. 4.2 и 4.3.
В первом случае (рис. 4.2) порождаемые выборочные переменные— это переменные, соответствующие правому краю маски, т. е.  ; остальные выборочные переменные являются порождающими. Порождение данных в матрице данных происходит слева направо. Пусть порождающая функция поведения
; остальные выборочные переменные являются порождающими. Порождение данных в матрице данных происходит слева направо. Пусть порождающая функция поведения  , представленная в виде (4.20), определяется уравнениями
, представленная в виде (4.20), определяется уравнениями
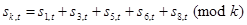
при  , Множества состояний порождаемых переменных определяются этими уравнениями, а множества состояний порождающих переменных — их положением в маске. Например, множество состояний порождаемой переменной
, Множества состояний порождаемых переменных определяются этими уравнениями, а множества состояний порождающих переменных — их положением в маске. Например, множество состояний порождаемой переменной  — это 0, 1, 2, 3, так как уравнение для
— это 0, 1, 2, 3, так как уравнение для  берется по модулю 4; порождающая переменная
берется по модулю 4; порождающая переменная  имеет то же множество состояний, что и s4, так как обе эти переменные определены через одну и ту же переменную представляющей системы (т. е.
имеет то же множество состояний, что и s4, так как обе эти переменные определены через одну и ту же переменную представляющей системы (т. е.  ).
).
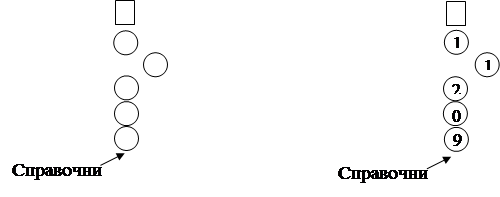 |
| t= | 1 | 2 | 3 | 4 | 5 | 6 | … | t= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
|
| 1 | 1 |
| 1 | 1 | 1 | |||||||||||
|
| 1 | 1 |
| 1 | 1 | 1 | |||||||||||
|
| 1 | 1 | 4 |
| 1 | 1 | 5 | 2 | |||||||||
|
| 1 | 1 | 5 |
| 1 | 1 | 5 | 3 | |||||||||
|
| 5 |
| 5 | 9 |
а) б)
|
| 1 | 2 | 3 | 4 | 5 | 6 | … | t= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
|
| 1 | 1 | 1 |
| 1 | 1 | 0 | ||||||||||
|
| 1 | 1 | 1 |
| 1 | 1 | 1 | 2 | 0 | ||||||||
|
| 1 | 1 | 5 | 2 |
| 1 | 1 | 5 | 2 | 0 | 4 | ||||||
|
| 1 | 1 | 6 | 0 |
| 1 | 1 | 5 | 0 | 5 | 4 | ||||||
|
| 6 | 9 | 4 |
| 5 | 9 | 4 | 4 |


в) г)
| t= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | … |
|
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||
|
| 1 | 1 | 1 | 2 | 0 | 1 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | 2 | 2 | |||
|
| 1 | 1 | 5 | 2 | 0 | 4 | 2 | 5 | 0 | 5 | 5 | 6 | 2 | 5 | 0 | 3 | 3 | |
|
| 1 | 1 | 5 | 0 | 5 | 4 | 0 | 3 | 7 | 3 | 3 | 4 | 7 | 3 | 5 | 1 | 1 | |
|
| 5 | 9 | 4 | 4 | 9 | 2 | 7 | 2 | 2 | 3 | 6 | 2 | 4 | 0 | 0 |
|
д)
Рис. 4.2. Данные, порожденные в порядке возрастания значения параметра t (Пример 3.1).
Первой осмысленной позицией маски на матрице данных (позиция определяется положением справочника маски) является позиция t=3; позиции t=1 и t=2 смысла не имеют, так как состояния некоторых выборочных переменных для этих позиций не определены ( не входит в множество Т). Начальное условие состоит из шести элементов матрицы данных:
не входит в множество Т). Начальное условие состоит из шести элементов матрицы данных:  . Пусть, например, все эти элементы равны 1. Еще пять элементов матрицы данных —
. Пусть, например, все эти элементы равны 1. Еще пять элементов матрицы данных — — не могут быть порождены, а могут быть заданы пользователем, но для порождения данных эти переменные не нужны. На рис. 4.2,а,б,в,г подробно показано порождение состояний соответственно для t = 3, 4, 5, 6; кружками обведены порожденные состояния. На рис. 4.2.д показано начальное условие и несколько больший фрагмент порожденной матрицы данных.
— не могут быть порождены, а могут быть заданы пользователем, но для порождения данных эти переменные не нужны. На рис. 4.2,а,б,в,г подробно показано порождение состояний соответственно для t = 3, 4, 5, 6; кружками обведены порожденные состояния. На рис. 4.2.д показано начальное условие и несколько больший фрагмент порожденной матрицы данных.
|
| … | 94 | 95 | 96 | 97 | 98 | 99 | t= | … | 93 | 94 | 95 | 96 | 97 | 98 | 99 | ||
|
| 1 | 1 |
| 1 | 1 | 1 |
| |||||||||||
|
| 1 | 1 |
| 1 | 1 | 1 |
| |||||||||||
|
| 5 | 1 | 1 |
| 5 | 1 | 1 |
| ||||||||||
|
| 5 | 1 | 1 |
| 5 | 1 | 1 |
| ||||||||||
|
| 5 |
| 5 |
|
а) б)
|
| … | 93 | 94 | 95 | 96 | 97 | 98 | 99 | t= | … | 93 | 94 | 95 | 96 | 97 | 98 | 99 | ||
|
| 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| ||||||||
|
| 3 | 1 | 1 | 1 |
| 2 | 3 | 1 | 1 | 1 |
| ||||||||
|
| 3 | 3 | 5 | 1 | 1 |
| 4 | 3 | 3 | 5 | 1 | 1 |
| ||||||
|
| 6 | 0 | 6 | 1 | 1 |
| 1 | 6 | 0 | 5 | 1 | 1 |
| ||||||
|
| 4 | 9 | 5 |
| 10 | 4 | 9 | 5 |
|
в) г)
| t= | … | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| |||
| 1 | 2 | 3 | 3 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 3 | 2 | 3 | 1 | 1 | 1 |
| ||
| 5 | 3 | 2 | 5 | 5 | 5 | 2 | 3 | 0 | 3 | 4 | 3 | 3 | 5 | 1 | 1 |
| |||
| 2 | 6 | 2 | 8 | 8 | 5 | 8 | 0 | 3 | 6 | 1 | 6 | 0 | 5 | 1 | 1 |
| |||
| 9 | 7 | 0 | 4 | 9 | 6 | 6 | 5 | 8 | 9 | 1 | 4 | 10 | 4 | 9 | 5 |
|
|
Рис. 4.3. Данные, порожденные в порядке убывания значения параметра t (Пример 3.1).
Лекция "32 - Инженерно-геологические процессы" также может быть Вам полезна.
|
 . Данные в матрице данных порождаются справа налево. Предположим теперь, что
. Данные в матрице данных порождаются справа налево. Предположим теперь, что  определяется уравнениями
определяется уравнениями 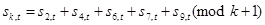
при k = 1, 3, 5, 8, 10. Порождение данных при t = 98, 97, 96, 95 подробно показано на рис.4.3,а, б, в и г. На рис. 4.3,д показано начальное условие и несколько больший фрагмент порожденной матрицы.
К.Р. № 10
Для некоторой системы с поведением, опишите функции поведения. Приведите пример процедуры порождения данных.



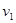
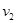
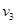
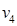
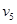



 t=
t=




 t=
t=