Число маха. Коэффициент скорость. Газодинамические функции

Лекция 6.

Число маха. Коэффициент скорость. Газодинамические функции.

Температура движения газа в одномерном потоке в общем случае различна в различных сечениях. В Каждом сечении местная скорость звука различна. Отношение скорости газа в данном сечении к местной скорости звука обозначают M и называют числом маха

 (1.40)

где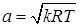

T – температура газа в рассматриваемом сечении.

Газ считаем идеальным.

Режим при котором число маха = 1, т.е. скорость частиц газа равна местной скорости звука, называется критическим

Рекомендуемые материалы

Этому режиму соответствует определенная температура - , критическое давление – p_кр, критическая плотность - .

Критические параметры идеального газа однозначно связаны с параметрами торможения, в частности с температурой торможения. Как было показано ранее в теплоизолированном потоке температура торможения во всех точках потока одинакова, поэтому критическая скорость для данного потока есть величина постоянная.

Введем еще одно понятие:

Отношение скорости газа в некоторой точке потока к критической скорости обозначают  и называют коэффициентом скорости.

  (1.41)

Получим связь между параметрами потока и параметрами торможения при наличии скорости:

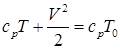
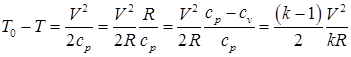
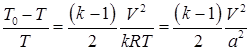
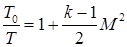
  (1.42)

Зависимость (1.42) выражает отношение температуры газа в потоке к температуре торможения функцией от числа маха.

Если поток энергетически изолирован, то связь между параметрами газа при их изменении по потоку может быть установленна уравнением адиабаты Пуассона.

Используя ранее полученные зависимости, выразим отношения давления и плотности газа в потоке к соответствующим значениям параметров торможения функцией от числа маха.

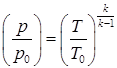
  (1.43)

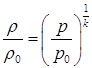
  (1.44)

Если M=1 из (1.42), (1.43), (1.44) (т.е. в критическом режиме течения) получим формулы, определяющие величины критических параметров газа.

  (1.45)

Функции , ,  называют газодинамическими функциями с их использованием решаются многие задачи газодинамических расчетов.

Газодинамические функции, аргументом которых является число маха удобны при решении задач внешнего обтекания тел газовым потоком.

Если решаемая задача, связана с течением газа по каналам в различных устройствах, то более удобны газодинамические функции, аргументом которых является .

Ещё посмотрите лекцию "Письменная литература" по этой теме.

  (1.46)

  (1.47)

Заметим, что если M=1, то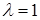

Если , то

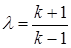
  (1.48)

В литературе приводятся таблицы газодинамических функций с аргументами , M.