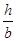Кручение стержней
8. Кручение стержней
Это такой вид нагружения, при котором в поперечном сечении стержня возникают только крутящие моменты, отличные от 0. а N = Qx = Qy = Mx = My = 0.
Стержень, работающий на кручение, называется валом.
8.1 Кручение круглых стержней
Три стороны задачи о кручении.
Рассмотрим вал, находящийся под действием крутящих моментов (рис. 8.1).

Рис. 8.1 Вал
1. Статическая сторона задачи:
Рекомендуемые материалы
Mкр (z) = M,
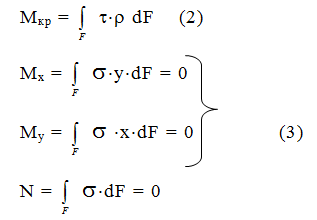
Анализируя формулы (3), приходим к выводу, что нормальные напряжения в нормальных сечениях s = 0.
Найдем закон изменения касательных напряжений “t” в поперечном сечении бруса.
2. Геометрическая сторона задачи.
Она связана с применением гипотезы Бернулли (плоских сечений)
Экспериментально установлено, что при кручении круглого бруса ось стержня не меняет своей длины и формы, а поперечные сечения, плоские и нормальные к плоскости бруса до приложения крутящего момента, остаются такими же после приложения крутящего момента, и поворачиваются друг относительно друга. Физическая модель резинового бруса: поперечные сечения закручиваются друг относительно друга.
Выделим участок бруса длиной dz и имеющего радиус r (рис. 8.2).
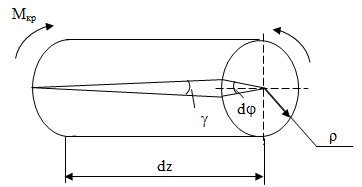
Рис. 8.2 Участок бруса
Пусть левая часть неподвижна.
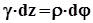
 (4)
(4)
j - абсолютный угол поворота
q - относительный угол закручивания (поворота), приходящийся на единицу длины
g - угловая деформация
3. Физическая сторона задачи
Заключается в применении закона Гука.
Закон Гука для угловых деформаций:
t = g×G (5), G – модуль сдвига (модуль упругости II–го рода)
Gстали = 8×104 МПа = 8×1010 Па
Объединяя три стороны задачи, получаем:
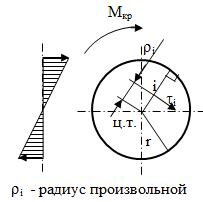
Рис. 8.3 Эпюра касательных напряжений
из (4), получаем g = r×q => (5) Mкр =  t×r dF
t×r dF
 t = r×s× G (6) => (2) Mкр =
t = r×s× G (6) => (2) Mкр =  r2×q×G dF (2) = q×G
r2×q×G dF (2) = q×G  r2 dF
r2 dF
const Ip
Ip =  r2 dF – полярный момент инерции
r2 dF – полярный момент инерции
Ix = Iy = p×D4/64; Ip = 2×Ix = 2×Iy = p×D4/32
q = Mкр/ (G×Ip) (7)
(7)®(6) => t = (Mкр×r×G)/Ip= (Mкр×r)/Ip
t = (Mкр×ri)/Ip (8)
Анализируя формулу (8), делаем вывод, что касательные напряжения при кручении распределяются по нормальному закону (рис. 8.3).
tmax возникают при r = 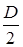
Wp = Ip/(D/2) – полярный момент сопротивления
Для круглого сплошного сечения: Wp = (p×D3)/16
Тогда tmax = Mкр/Wp; Мкр/Wк  [t], где Wк – момент сопротивления при кручении, равный в данный момент Wp.
[t], где Wк – момент сопротивления при кручении, равный в данный момент Wp.
tmax = Mкр/Wк£ [t] – условие прочности при кручении.
8.1.1 Геометрические характеристики Ip и Wp

Анализируя эпюру t, мы видим, что в центре сечение не нагружено, т.о. рациональным сечением является не сплошной вал, а кольцо.
Задача: сопоставить по металлоемкости два равноправных сечения (рис. 8.4).
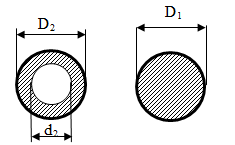
Рис. 8.4 Полое и сплошное сечения вала
Равнопрочные:
tmax1 = tmax2
tmax1 = Мкр/Wp1
tmax2 = Мкр/Wp2
Мкр/Wp1 = Мкр/Wp1Þ 1/Wp1 = 1/Wp1
(p×D31)/16 = [(p×D32)/16]×(1–(d24/D24))Þ1/D13 = 1/(D23(1–0.84));
0.59 D23 = D13;
D1 = D×0.839.
Сопоставляем сечения 1 и 2 по металлоемкости:
F1/F2 = [(p×D12)/4]/[((p×D22)/4)–(1–d22/D22)] = 1.9.
8.2 Кручение прямоугольных стержней
При кручении прямоугольных стержней гипотеза плоских сечений не выполняется, так как сечения искривляются - депланируют. Задача о кручении прямоугольных стержней решается в теории упругости.
Готовые формулы
h>b

Рис. 8.5 Эпюра касательных напряжений для некруглых стержней
В углах и центре тяжести 0
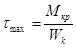

где Wk = a×b2×h - момент сопротивления при кручении
Ik = b×b3×h -
a, b, g -коэффициенты, зависят от соотношения 
Некоторые значения коэффициентов a, b, g.
|
| |||||||
| 1 | 1,5 | 1,75 | 2 | 2,5 | 3 | 10 | |
| a | 0,208 | 0,231 | 0,239 | 0,246 | 0,256 | 0,267 | 0,313 |
| b | 0,141 | 0,196 | 0,214 | 0,229 | 0,249 | 0,263 | 0,313 |
| g | 1 | 0,869 | 0,82 | 0,795 | 0,766 | 0,753 | 0,742 |
Абсолютный угол закручивания вала, состоящего из n участков - j.






Пример (К-1)
Дано (рис. 8.6)




Решение

первый участок


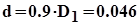
второй участок



третий участок
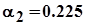



так как мы приняли за диаметр трубки диаметр D1, то пересчитаем момент сопротивления

В лекции "7 - Принципы управления" также много полезной информации.
найдем угол закручивания стержня

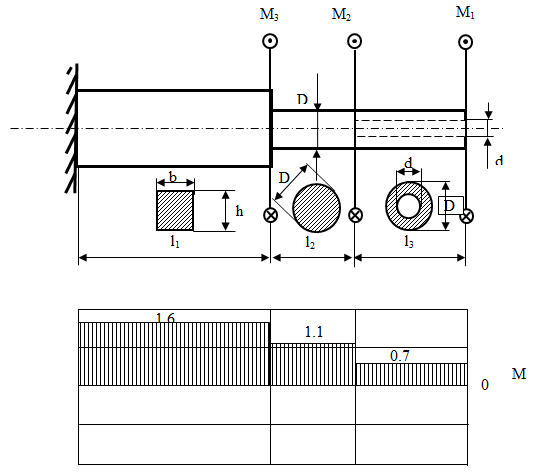
Рис. 8.6 Эпюра крутящих моментов

Рис. 8.7 Эпюра касательных напряжений для различных сечений стержня