Геометрические характеристики плоских сечений

9. Геометрические характеристики плоских сечений

Рассмотрим произвольное плоское сечение (рис. 9.1). Выделим элементарную площадку dF и определим ее характеристики.

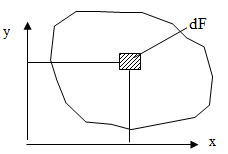
Рис. 9.1 Произвольное плоское сечение тела

Статистический момент инерции сечения.

Называется S_x и S_y относительно осей x и y

            интегральная сумма произведения элементарных площадок на их расстояние до оси.

  =>  [S] = м³

Используется для определения центра тяжести касательных напряжений при изгибе.

Рекомендуемые материалы

Координаты центра тяжести сечения

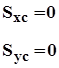
Если фигура состоит из нескольких простых

Осевой момент инерции сечения.

   [м⁴]

   [м⁴]

Главная характеристика при расчетах на изгиб.

Центробежный момент инерции скольжения – интегральная сумма произведения элементарных площадок на расстояние до осей.

  [м⁴]

Полярный момент инерции.

   [м⁴]

Радиус инерции.

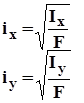
Осевой момент сопротивления.

W_x, W_y   [м²]

Для сечения, имеющего две оси симметрии:

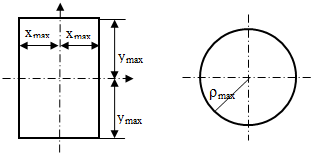
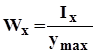
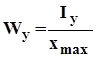
Для сечения, имеющего одну ось симметрии:

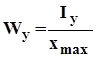
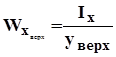
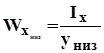
   полярный момент сопротивления

Пример

         dF = b×dy

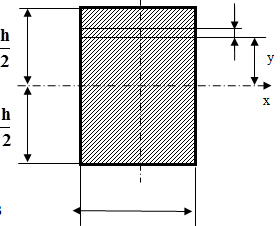
I_x = ?

тогда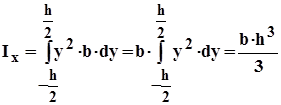  

9.1 Геометрические характеристики простых сечений

9.2 Параллельный перенос осей

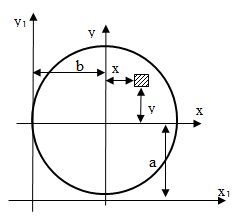
Рис. 9.2 Параллельный перенос осей

Дано: F, a, b, I_x, I_y, I_xy; (рис. 9.2)

Найти: I_x1, I_y1, I_x1y1;

Решение:

Если оси x и y - центральные, то Sx=Sy=0 и формулы имеют вид:

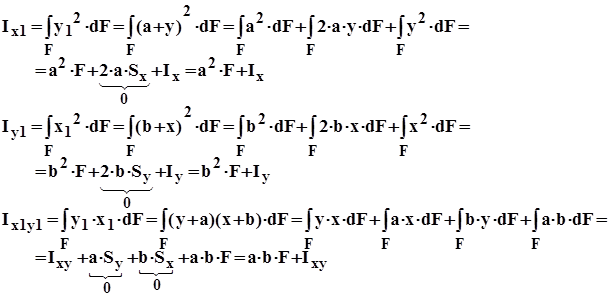
В общем виде формулы параллельного переноса имеют вид:

 n - число составных частей

9.3 Поворот осей

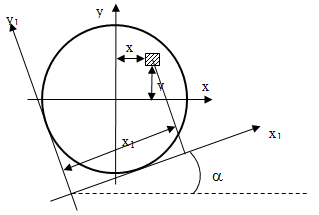
Рис. 9.3 Поворот осей

Дано: I_x, I_y, I_xy, a (рис. 9.3)

Найти:I_x1, I_x2, I_x1y1

Решение:

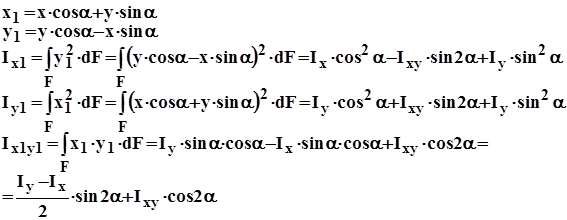
Исследуем на экстремум I_x1

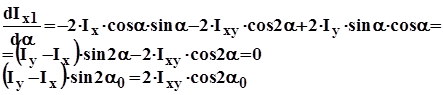
 - ось максимума

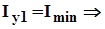
 - ось минимума

 - сумма осевых моментов инерции при повороте осей инвариантна (=const)

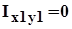
Оси, относительно которых центробежный момент равен 0, называются главными. Моменты инерции относительно этих осей принимают максимальные и минимальные значения:

,  - главные моменты инерции

Главные оси, u, v, проходящие через центр тяжести сечения, называются главными центральными.

В лекции "Анкета для подростков" также много полезной информации.

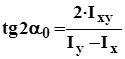
Главные центральные моменты сечения:

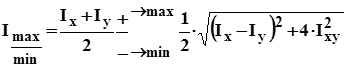
Если сечение обладает симметрией, то оси симметрии и являются главными осями.