Плазма в магнитном поле
лекция 2
ПЛАЗМА В МАГНИТНОМ ПОЛЕ
1. «Вмороженность» магнитного поля
Внешнее магнитное поле оказывает существенное влияние на свойства плазмы. Рассмотрим магнитный поток  через поверхность, опирающуюся на замкнутый контур
через поверхность, опирающуюся на замкнутый контур  , проведённый в плазме. Этот магнитный поток может изменяться либо за счёт изменения контура, каждый элемент которого движется с локальной скоростью
, проведённый в плазме. Этот магнитный поток может изменяться либо за счёт изменения контура, каждый элемент которого движется с локальной скоростью  плазмы. Скорость изменения магнитного потока за счёт движения контура определяется выражением:
плазмы. Скорость изменения магнитного потока за счёт движения контура определяется выражением:
 , (1)
, (1)
где  – элемент площади, описываемый элементом контура
– элемент площади, описываемый элементом контура  при его движении со скоростью
при его движении со скоростью  .
.
Осуществляя циклическую перестановку векторов, получим:
 ,
,
используя далее теорему Стокса имеем:
 . (2)
. (2)
Скорость изменения магнитного потока за счёт изменения магнитного поля во времени запишется так:
Рекомендуемые материалы
 . (3)
. (3)
Суммируя (2) и (3) и учитывая уравнение Максвелла  , получим:
, получим:
 . (4)
. (4)
Правая часть (4) обращается в нуль, если выполняется равенство:
 , (5)
, (5)
при этом  . Таким образом, при выполнении (5) магнитное поле оказывается «вмороженным» в плазму: магнитный поток
. Таким образом, при выполнении (5) магнитное поле оказывается «вмороженным» в плазму: магнитный поток  через любой замкнутый контур, элементы которого движутся с локальной скоростью плазмы, остаётся постоянным. Условие (5) соответствует условию идеальной проводимости плазмы. «Вмороженность» магнитного потока в случае идеальной проводимости можно объяснить следующим образом: согласно закону электромагнитной индукции Фарадея при изменении магнитного потока через поверхность, опирающуюся на замкнутый контур, в контуре возникает ЭДС. В случае контура из идеального проводника ЭДС должна была возбуждать бесконечно большой ток, что невозможно. Следовательно, идеальный контур должен увлекать за собой магнитные силовые линии так, как если бы они были в него «вморожены».
через любой замкнутый контур, элементы которого движутся с локальной скоростью плазмы, остаётся постоянным. Условие (5) соответствует условию идеальной проводимости плазмы. «Вмороженность» магнитного потока в случае идеальной проводимости можно объяснить следующим образом: согласно закону электромагнитной индукции Фарадея при изменении магнитного потока через поверхность, опирающуюся на замкнутый контур, в контуре возникает ЭДС. В случае контура из идеального проводника ЭДС должна была возбуждать бесконечно большой ток, что невозможно. Следовательно, идеальный контур должен увлекать за собой магнитные силовые линии так, как если бы они были в него «вморожены».
Так как пересечение линий индукции магнитного поля приводит к возникновению ЭДС индукции, то «вмороженность» магнитного поля означает, что заряженные частицы идеально проводящей плазмы движутся вдоль линий индукции магнитного поля.
Отметим, что «вмороженность» магнитного поля в плазму в значительной степени определяет картину нарастания магнитного поля при сжатии плазмы и имеет большое значение в ряде прикладных задач, например, в астрофизике.
2. Скиновая длина и скиновое время
Если учесть конечную проводимость, то условие (5) уже не будет удовлетворяться. В системе координат, связанной с плазмой, будут действовать электрические поля, вызывающие электрические токи. В приближении магнитной гидродинамики ток считается подчиняющимся закону Ома:
 , (6)
, (6)
здесь  – проводимость (в этом приближении считается скалярной величиной).
– проводимость (в этом приближении считается скалярной величиной).
Для плазмы, находящейся в магнитном поле, закон Ома (6) является приближённым, так как он не учитывает анизотропию проводимости.
Из (6) следует, что:
 .
.
Воспользуемся уравнением Максвелла, пренебрегая токами смещения:
 .
.
После подстановки имеем:
 .
.
Применим операцию  к обеим частям полученного равенства:
к обеим частям полученного равенства:
 .
.
Воспользуемся уравнением Максвелла  и формулой векторного анализа
и формулой векторного анализа  , и учитывая, что
, и учитывая, что  , получим:
, получим:
 . (7)
. (7)
Рассмотрим простейший случай, когда движение вещества отсутствует, то есть  . Тогда:
. Тогда:
 . (8)
. (8)
Это уравнение тождественно по виду с уравнением диффузии (второй закон Фика), роль коэффициента диффузии играет величина:
27 Метод Бубнова - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
 , (9)
, (9)
обратно пропорциональная проводимости плазмы. Можно сказать, что из-за конечной проводимости магнитное поле как бы просачивается сквозь плазму по диффузионному закону с коэффициентом диффузии  .
.
Глубина просачивания поля в течение заданного времени 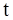 :
:

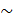
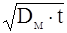
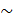
 .
.
Для переходного процесса время 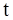 порядка обратной частоты
порядка обратной частоты  и, следовательно:
и, следовательно:

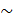
 . (10)
. (10)
называют толщиной скин-слоя, а в более общем случае непериодических процессов выражение (10) называют выражением для скиновой длины. Можно оценить время просачивания магнитного поля на заданную глубину  :
:
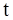
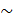
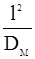
 ,
,
эту величину называют скиновым временем.



















