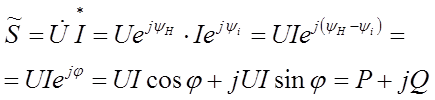Параллельные соединения элементов r, L, C

2.9 Параллельные соединения элементов r, L, C.

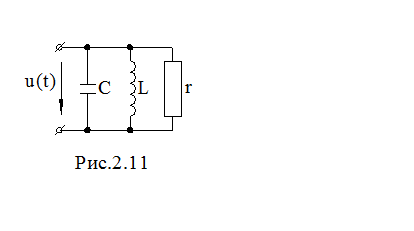
Для схемы рис. 2.11. составим уравнение по первому закону Кирхгофа для мгновенных значений:

                  (10)

Если  , то

(11)

Здесь

 - активная проводимость,

 - индуктивная проводимость.

Рекомендуемые материалы

Единица измерения проводимостей - сименс (Сим).

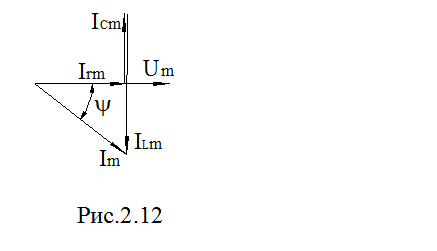
Векторная диаграмма токов приведена на рис. 2.12.

Уравнение (11) в комплексной форме:

         (12)

Здесь

 - комплексная проводимость или комплекс проводимости,

 - модуль комплекса проводимости

 - фаза комплекса проводимости.

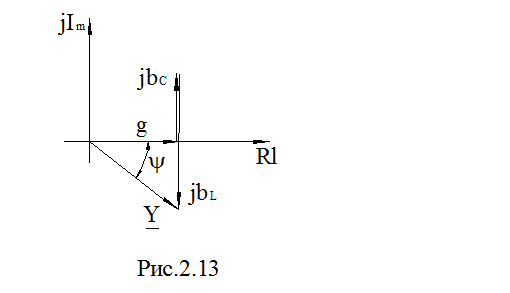
Проводимости  образуют треугольник проводимости, рис. 2.13.

Комплексная векторная диаграмма токов для уравнения (12) приведена на рис. 2.14.

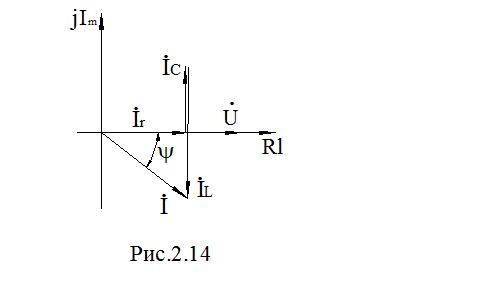
Пример 1.

Для схемы, приведенной на рис. 2.15.

Задано:

,

L=6,37  мГн, С=796  мкФ,    f=50 Гц,

, , 

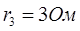
Определить токи.

Решение.

Воспользуемся комплексным методом расчета. Запишем комплексы сопротивлений для каждой ветви:

,

.

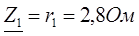
Входное сопротивление цепи:

Входной ток:

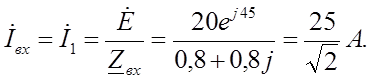
Определим токи  и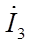

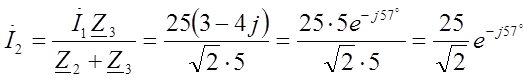
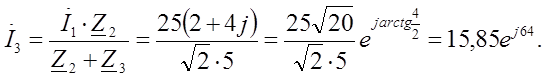
Мгновенные значения токов запишем в виде:

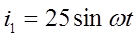
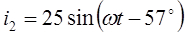
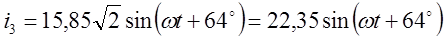
Пример 2.

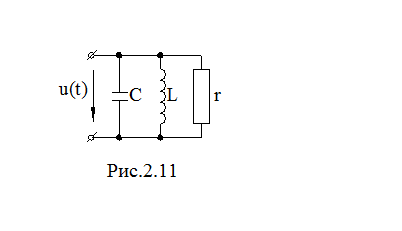
Для схемы рис. 2.11 определить сдвиг по фазе между входным током и напряжением, если  Ом, Ом,  Ом.

Решение:

комплекс тока:

Фаза напряжения принята за ноль, а фаза тока получилась равной . Сдвиг по фазе между током и напряжением .

2.9.1. Мощность в цепи синусоидального тока. Комплексная мощность.

Пусть в цепи рис. 2.7 ток равен  .Мгновенное напряжение будет сдвинуто по отношению к току на угол , отличный от 0 и .Мгновенная мощность для этой цепи примет вид:

(13)

Выразим сопротивления r  и  через модуль сопротивления Z :

,       ,             (14)

Подставим (14) в (13), получим

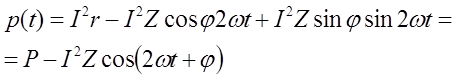
Временные диаграммы i(t), u(t), p(t) приведены на рис. 2.16.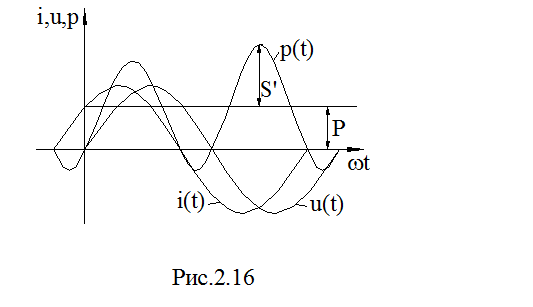

Мощность p(t) имеет постоянную составляющую, т.е. среднюю мощность, или активную мощность:

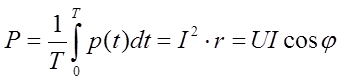
и переменную составляющую. Амплитуда переменной составляющей  называется полной мощностью, измеряется в вольт-амперах, (ВА).

Мощности P и S связаны по закону треугольника мощностей, рис 2.17.

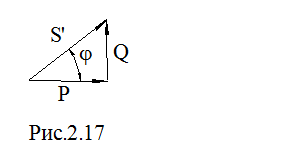
Третья составляющая в этом треугольнике – мощность реактивная .

Реактивная мощность измеряется в вольт-амперах реактивных,().Полезная мощность измеряется ваттметром.

Пример.

График мгновенной мощности p(t) приведен на рис. 2.19.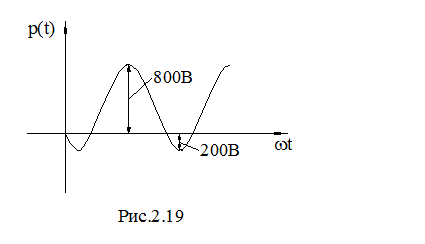

Максимальное и минимальное значения мощности соответственно равны 800 и 200 ВА. Определить полную активную и реактивную мощности цепи.

Решение:

Размах значений мощности 1000 ВА, амплитудное значение 500 ВА, это полная мощность S. Среднее значение мощности P=800-500=300 Вт. Реактивная мощность .

Отношение активной мощности к полной (рис. 2.17) равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности

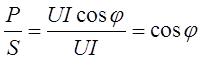
Для лучшего соотношения между мощностью электрической машины и других приборов и их габаритными размерами коэффициент мощности стремятся сделать максимально возможным.

Высокий коэффициент мощности желателен для уменьшения потерь при передаче энергии по линиям.

Рекомендуем посмотреть лекцию "Часть 6".

Чтобы выразить мощность через комплексы токов и напряжений воспользуемся следующим соображением.

Пусть заданы комплексы и  .

Активная мощность должна быть равна, где .

Отсюда следует, что при определении комплекса мощности фаза тока должна быть взята с обратным знаком, т.е. комплекс тока должен быть заменен на сопряженный.

Полная комплексная мощность