Применение теоремы Гаусса
Применение теоремы Гаусса.
1. Длинная, равномерно заряженная нить.
 Вектор
Вектор  перпендикулярен к нити.
перпендикулярен к нити.
Посчитаем поток  :
:
Воспользуемся теоремой Гаусса:
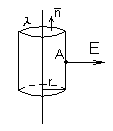
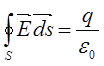
Нужно придумать такую замкнутую поверхность, чтобы через ее часть поток был равен нулю, а в другой напряженность такую же, как и в точке А.
[ ] =
] =  - линейная плотность заряда
- линейная плотность заряда
В данном случае это цилиндр. Поток через его основание равен нулю, т.к. линии напряженности параллельны основанию.
Рекомендуемые материалы
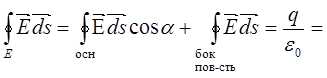
высоту цилиндра h задают. Во всех точках боковой поверхности напряженность одинаковая, вынося ее за интеграл:
 =>
=>
 - заряд, охваченный цилиндром.
- заряд, охваченный цилиндром.
=>  - напряженность поля, созданного длинной заряженной нитью в точке, расположенной на расстоянии r.
- напряженность поля, созданного длинной заряженной нитью в точке, расположенной на расстоянии r.
2.Бесконечно большая заряженная поверхность.
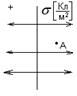
Нас интересует поле в точке А. Снова «придумываем» цилиндр:
 (6)
(6)
 , т.к.
, т.к.  параллелен боковой поверхности цилиндра.
параллелен боковой поверхности цилиндра.
 так как во всех точках оснований из соображения симметрии
так как во всех точках оснований из соображения симметрии  одинаково, то можно вынести за интеграл:
одинаково, то можно вынести за интеграл:
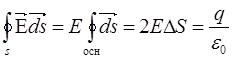
где q- заряд, охватываемый цилиндром =>
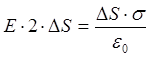
 =>
=>  (7)
(7)
вывод: исходя из (7),  не зависит от расстояния, т.е. поле однородно.
не зависит от расстояния, т.е. поле однородно.
3. Конденсаторы
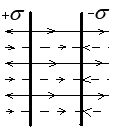
Две бесконечно большие поверхности.
На рисунке силовые линии, созданные “+”- обозначим сплошными, а созданные “ – ” - пунктирными.
Снаружи поля компенсируются, а внутри – суммируются.
Исходя из пункта 2, напряженность поля конденсатора:
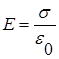
 Упражнение:
Упражнение:
Лекция "Особенности использования ресурсов информационных систем" также может быть Вам полезна.
Шар. Заряд q равномерно распространен по объему.
Найти напряженность в точке А.


















