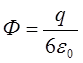Теорема Гаусса

Теорема Гаусса.

Поток вектора  через замкнутую поверхность S, равен суммарному заряду, охваченному этой поверхностью, деленному на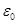

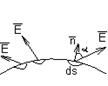
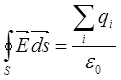
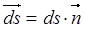
где ds – величина площадки

в случае замкнутой поверхности, – внешняя нормаль к ней.
 

В пределах каждой площадки вектор  неизменен. Суммируя все скалярные произведения и интегрируя по всей площади, получим поток.

Доказательство:

1) берем точечный заряд +q, окружаем его сферой S. Считаем поток через сферу. По определению:

Рекомендуемые материалы

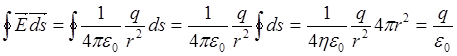
(т.к. площадь сферы ) что и требовалось доказать.

2) теперь рассмотрим произвольную замкнутую поверхность:

Внутри этой поверхности S нарисуем сферу

(5) – телесный угол

площадка ds настолько мала, что r – одинаково.

Умножим (5) на :

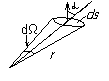
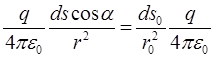
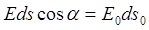
 (равенство потоков) сложим все dФ:

Ф= что и требовалось доказать.

3) случай n зарядов

Поток через S:

Если заряд находится вне поверхности, он потока не создает. (один поток со знаком +, другой со знаком -)

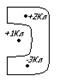
Задача:

 Чему равен поток через эту поверхность?

Решение:, т.к. заряд +1Кл потока не создает

Бесплатная лекция: "Элементы теории компиляции" также доступна.

  Задача:

  В центре куба заряд q. Чему равен поток через одну грань?

Решение: