Теорема Гаусса. Дифференциальная формулировка закона Кулона
§ 1.4. Теорема Гаусса. Дифференциальная формулировка закона Кулона.
Введем понятие ”потока вектора напряженности сквозь поверхность площади 
” (рис.1.6).
. (1.10)
Направление для поверхности, охватываемой контуром 
, выбирается по правилу буравчика. Для замкнутой поверхности:
. (1.11)
Для замкнутой поверхности в качестве положительного всегда выбирается направление в сторону внешней нормали.
Определим поток вектора напряженности от точечного заряда q сквозь замкнутую поверхность, окружающую заряд.
По закону Кулона напряженность поля точечного заряда:
.
Рекомендуемые материалы
Тогда, подставив в (1.11), получим:
. (1.12)
Учтем, что 
, т.е. выражение в скобках представляет собой проекцию на радиус-вектор. По определению, 
- это телесный угол, под которым элемент 
виден из начала отсчета радиуса – вектора (рис.1.7).
Тогда
. (1.13)
Поток сквозь замкнутую поверхность вектора напряженности электрического поля равен заряду, заключенному внутри поверхности.
Если заряд находится вне замкнутой поверхности, то формула (1.12) не изменяется. Но теперь подынтегральное выражение принимает положительные значения в тех точках поверхности, где угол
, 
и отрицательные значения, когда:
, 
.
Поэтому (см. рис.1.8):
.
В этом случае 
.
Обобщая, запишем:
. (1.14)
Эта формула называется теоремой Гаусса для точечного заряда.
Обобщение на систему точечных зарядов производится с помощью принципа суперпозиции. Для системы точечных зарядов 
:
, 
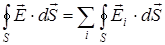
Для 
верна теорема Гаусса для точечного заряда, т.е.
,
где V - показывает, что суммируются лишь заряды, находящиеся внутри объема. Общая формула, выражающая фундаментальную теорему Гаусса, запишется теперь так:
. (1.15)
Поток вектора напряженности поля 
через произвольную замкнутую поверхность равен полному заряду, расположенному внутри этой поверхности.
При непрерывном изменении заряда внутри объема заключен заряд:
,
где интегрирование производится только по объему, заключенному внутри замкнутой поверхности.
Физическая основа справедливости теоремы Гаусса связана с законом Кулона, так как для точечного заряда, к которому мы приводим вывод, в любом случае справедливой считается зависимость:
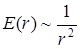
Таким образом, теорема Гаусса в вышеприведенном виде – это интегральная формулировка закона Кулона.
Запишем теорему Гаусса в дифференциальной форме.
В математике вводится понятие дивергенции вектора 
:
, (1.16)
где 
- бесконечно малая замкнутая поверхность, ограничивающая объем 
. Показывается, что:
, (1.17)
или, если ввести векторный оператор 
(набла):
, (1.18)
. (1.19)
Разделив левую и правую части формулы (1.15) на и учитывая, что объемная плотность заряда 
, получим:
, (1.20)
- дифференциальная форма теоремы Гаусса.
Поток вектора из элементарного объема равен объемной плотности заряда в нем.– Это локальная формулировка теоремы Гаусса.
Из формулировки следует понятие источника и стока . Вектор начинается там, где 
, т.е. 
; оканчивается там, где 
, 
(рис.1.9).
Силовой линией электрического поля называется линия, касательная к которой в каждой точке совпадает с вектором напряженности поля.
Понятие “силовая линия”, как и понятие “поля”, впервые было введено Фарадеем. Силовые линии можно “увидеть”, если продолговатые кристаллики какого-либо диэлектрика (например, хинина) взболтать в вязкой жидкости (касторовом масле) и поместить в электрическое поле.
Примеры.
1. Найти поле сферы радиуса R, равномерно заряженной по поверхности зарядом Q.
Ясно, что вектор направлен вдоль радиуса сферы и одинаков по модулю во вcех точках сферы радиуса r. Такая конфигурация поля показывает, что в качестве замкнутой поверхности необходимо выбрать сферу радиуса r.
Если 
, то:
Þ 
. (1.21)
Если 
, тогда:
. (1.22)
График E(r) показан на рис.1.10. То, что внутри сферы 
, было использовано Кавендишем для экспериментальной проверки закона Кулона.
2. Найти поле плоскости, равномерно заряженной зарядом с поверхностной плотностью 
.
Ясно, что перпендикулярен поверхности. В симметричных относительно плоскости точках одинаков по модулю. Поэтому следует выбрать в качестве гауссовой поверхности цилиндр с площадью основания (см.рис.1.11).
,
,
(1.23).
Поток через боковую поверхность равен нулю, так как и взаимно перпендикулярны.
1. Найти поле равномерно заряженного по объему шара. Объемная плотность заряда 
.
В качестве гауссовой поверхности из соображения симметрии (см. пример 1) выберем сферу.
Если , то
,
.
Тогда:
"4.2.5. Регулирование" - тут тоже много полезного для Вас.
. (1.24)
Если , то внутри замкнутой поверхности заключен весь заряд сферы:
.
Тогда:
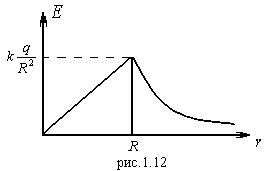
. (1.25)
Зависимость E(r) показана на рис.1.12.
