Теорема об изменении кинетической энергии
Лекция 5. Теорема об изменении кинетической энергии
5. 1. Работа силы
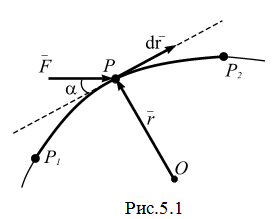
Пусть сила 
– равнодействующая всех сил системы, приложена к точке Р, а 
(dx, dy, dz) – элементарное перемещение точки Р вдоль ее траектории Р1 Р2 (рис. 5.1). Элементарной работой dА силы 
называют скалярное произведение
. (5.1)
Элементарная работа является скалярной величиной. Если 
- угол между силой и направлением перемещения 
, то выражение (5.1) можно представить в виде
, (5.2)
где 
- проекция силы на направление элементарного перемещения (или направление скорости точки).
Рекомендуемые материалы
Знак элементарной работы зависит от знака функции
. Если - острый угол, то 
, если - тупой угол, то 
, если 
, то 
.
Пусть точка Р совершает конечное перемещение из положения 
в положение 
, описывая дугу 
. Разобьем дугу на n произвольных малых участков, обозначив длину участка с номером k через 
. Тогда элементарная работа силы на k-м участке будет равна 
, а на всем пути от до - сумме работ на отдельных участках
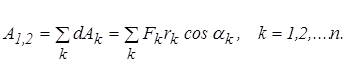
Точное значение работы получим, переходя к пределу, при условии, что число участков n неограниченно возрастает, а длина каждого участка 
убывает:
.
Такой предел называется криволинейным интегралом первого рода по дуге и записывается следующим образом
. (5.3)
Результат интегрирования является полной работой А силы F на рассматриваемом конечном перемещении вдоль пути .
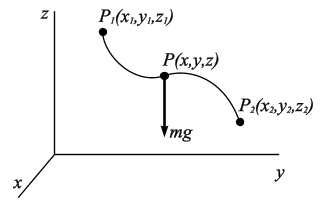
5. 1. 1. Работа силы тяжести
Пусть m – масса точки, g – ускорение свободного падения. Тогда
.
Вычисляя работу по формулам (5.1) и (5.3), имеем
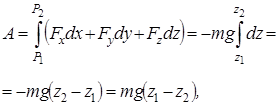
или
, (5.4)
где 
- высота опускания точки.
При подъеме точки 
, следовательно, 
.
5. 1. 2. Работа линейной силы упругости
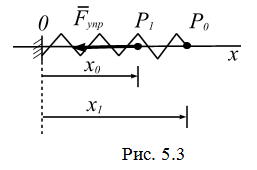
Пусть материальная точка Р движется вдоль оси Ох (рис. 5.3) под действием пружины, к которой она прикреплена. Если при 
, 
, то пружина деформирована и при малых отклонениях точки можно считать, что со стороны пружины к ней приложена сила упругости 
. Тогда работа силы упругости на перемещении x0 x1 будет равна
. (5.5)
Работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинения (или сжатий) пружины.
5. 1. 3. Элементарная работа сил, приложенных к твердому телу
Рассмотрим движение тела в плоскости. Пусть О – произвольно выбранная точка на твердом теле (рис.5.4). Назовем ее полюсом. Тогда движение тела в плоскости можно представить как сумму простейших: поступательного движения вместе с полюсом и вращение тела вокруг полюса. Тогда, скорость 
точки 
относительно неподвижной системы координат 
определится как геометрическая сумма двух скоростей
,
где 
- скорость полюса, 
- вектор угловой скорости твердого тела, 
– скорость Эйлера, т е. скорость точки при ее ращении вокруг полюса.
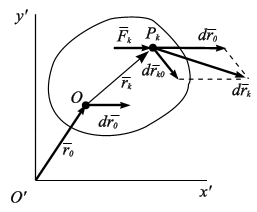
Будем представлять твердое тело как механическую систему, состоящую из N отдельных точек, взаимное расстояние между которыми не изменяется.
Вычислим смещение 
точки 
под действием силы 
:
, тогда 
.
Элементарная работа, согласно (5.1), запишется следующим образом
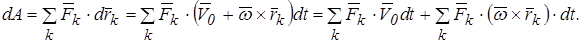
Воспользовавшись свойствами смешенного произведения векторов 
, перепишем последнее выражение в виде
. (а)
Пусть 
- равнодействующая всех сил, внешних и внутренних (рис5.4), приложенных в точке тела, т.е.
.
Тогда (а) запишется так
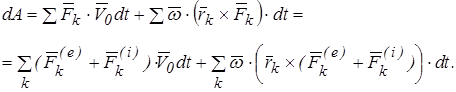
Согласно (3.1 и 3.2), главный вектор и главный момент внутренних сил системы равны нулю, получаем
, (5.6)
здесь: 
– главный вектор, 
– главный момент внешних сил относительно точки О.
Частные случаи
A. Поступательное движение твердого тела. Все точки тела имеют одинаковые перемещения (рис. 5.5, а) и по модулю, и по направлению, тогда, из (5.6), получим (здесь 
):
. (5.7)
B. Вращение твердого тела вокруг неподвижной оси. Пусть ось z проходит через полюс О (рис. 5.5б). Тогда 
, 
; из (5.6) получим
. (5.8)
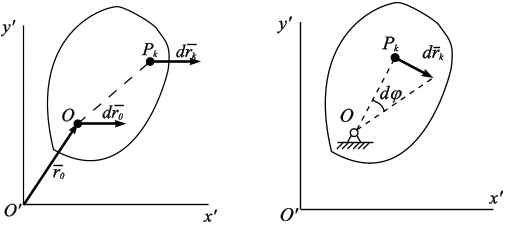
Пример. Катушка массой m и радиусом R приводится в движение постоянной силой F, приложенной в точке А (рис. 5.6). Катушка катится вправо без скольжения по шероховатой поверхности.
Вычислить работу всех внешних сил, если центр катушки переместился на расстояние 
, 
- коэффициент трения качения, 
- сила трения, r – радиус сердечника катушки, к которой приложена сила.
Решение. Катушка совершает плоское движение. Так как качение происходит без скольжения, то мгновенный центр скоростей находится в точке касания катушки с плоскостью, т.е. в точке Р (рис.5.6). Направим ось S по горизонтали вправо. В соответствии с направлением движения примем положительное направление угла поворота 
против хода часовой стрелки.
Пусть центр катушки С переместится на 
. При этом катушка повернется на угол 
. Тогда 
, откуда
.
Приняв точку Р за мгновенную ось вращения, вычислим элементарную работу по формуле (5.8):
(а)
Здесь: линии действия сил 
и mg пересекают ось вращения, поэтому 
; далее 
, где N – сила нормальной реакции.
Для определения искомой работы остается взять определенный интеграл от (а) в пределах от 0 до SА. Получим
.
5. 2. Силовое поле. Силовая функция. Потенциальная энергия
Предположим, что точка движется в некотором пространстве и на нее со стороны пространства действует сила, которая зависит от положения точки в этом пространстве, но не зависит от скорости движения точки. В этом случае говорят, что в пространстве задано силовое поле, а также, что точка движется в силовом поле. Соответствующие понятия для системы материальных точек аналогичны.
Силы, зависящие от положения точек их приложения, в механике встречаются часто. Например, сила упругости, приложенная к материальной точке, которая движется по горизонтальной прямой под действием пружины. Важнейшим примером силового поля в природе является гравитационное поле: действие Солнца на планету данной массы определяется в каждой точке пространства законом всемирного тяготения.
Силовое поле называется потенциальным, если существует скалярная функция U, зависящая только от координат 
, 
, 
точки -точки материальной системы (возможно, и от времени), такая, что
. (5.9)
Функция 
называется силовой функцией.
Рассмотрим свойства силовой функции.
Элементарная работа (5.1) связана с силовой функцией следующим образом
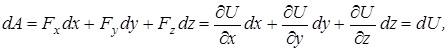
т.е.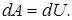 
Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции.
Полная работа силы 
на участке от точки
до точки 
(рис.5.1)
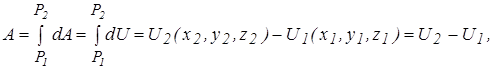
т.е. 
. (5.10)
Из полученных выражений следует, что
1. работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю;
2. работа силы в потенциальном силовом поле зависит только от положения конечной и начальной точек, но сам путь перемещения роли не играет.
Потенциальная энергия. Потенциальной энергией П в рассматриваемой точке силового поля Р называют работу, которую совершают силы поля, действующую на материальную точку при ее перемещении из точки Р в начальную точку 
1, т.е.
П=
или П=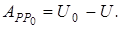
Свяжем силовую функцию U с потенциальной энергией. Имеем
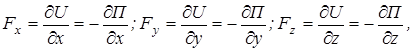
т.е.
, или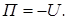 
Примеры вычисления потенциальной энергии
1. Однородное поле тяжести. Пусть m – масса точки; g – ускорение свободного падения. Тогда (рис. 5.2)
.
2. Силовое поле упругой пружины. Пусть материальная точка движется вдоль оси Ох (рис. 5.3) под действием пружины, к которой она прикреплена. Если при 
пружина не деформирована, то, полагая в формуле (5.5) 
, получим
.
5. 3. Кинетическая энергия
5. 3. 1. Кинетическая энергия системы. Теорема Кенига
Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. 
. Кинетическая энергия, является скалярной положительной величиной. В системе СИ, единицей измерения кинетической энергии является джоуль: 
.
Кинетической энергией механической системы называется сумма кинетических энергий всех точек, входящих в систему:
(5.11)
Скорости 
точек системы (5.1) определяются относительно неподвижной системы отсчета.
Совместим начало координат
с центром масс системы. Предположим, что механическая система вместе с системой координат движется поступательно относительно неподвижной системы координат 
(рис.5.7). Точка– точка системы.
Тогда, на основании теоремы о сложении скоростей, абсолютная скорость точки Рk. системы запишется так векторная сумма переносной и относительной скоростей:
, (а)
где 
– скорость начала подвижной системы координат (переносная скорость, т.е. скорость центра масс системы); 
– скорость точки Рk относительно подвижной системы координат Охуz (относительная скорость).
Подставляя (а) в формулу (5.11), получаем
(5.12)
Здесь 
- масса всей системы.
Радиус-вектор центра масс системы в подвижной системе координат определяется, согласно (2.1), – 
, откуда 
, т.е. 
. Поскольку начало координат О является центром масс системы, то 
, тогда 
, т.е. вторая сумма в выражении (5.12) равна нулю.
Таким образом, кинетическая энергия системы (5.12) имеет вид
(5.13)
Это равенство определяет теорему Кенига.
Теорема. Кинетическая энергия системы равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы, и кинетической энергии движения системы относительно центра масс.
5. 3. 2. Кинетическая энергия твердого тела
Твердое тело является частным случаем механической системы и рассматривается как непрерывно распределенная масса, тогда все суммы, входящие в выражение для кинетической энергии системы, переходят в интегралы. Так, для твердого тела формула (5.11) примет вид
. (5.14)
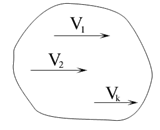
1. Кинетическая энергия твердого тела, двигающегося поступательно.
При этом виде движения скорости всех точек тела одинаковы (рис. 5.8). Вынося 
в формуле (5.14) за знак интеграла, получим
. (5.15)
Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела M на квадрат его скорости.
2. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси
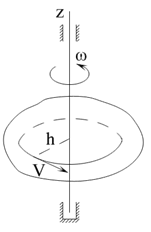
Модуль скорости V любой точки твердого тела, вращающегося вокруг неподвижной оси, равен 
, где 
- модуль угловой скорости твердого тела, 
- расстояние от точки до оси вращения z (рис. 5.9). Подставляя 
в формулу (5.14), получим
(5.16)
здесь 
– момент инерции твердого тела относительно оси z.
Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
3. Кинетическая энергия твердого тела при плоско – параллельном движении
При плоско – параллельном движении скорость любой точки тела состоит из геометрической суммы скорости полюса и скорости точки при вращении вокруг полюса. Пусть тело движется плоско в плоскости Oxy, тогда
|| 
. За полюс выбираем центр масс тела, тогда в формуле (5.13), скорость 
есть скорость точки k тела при ее вращении относительно полюса (центра масс) и равна 
, где 
расстояние k-ой точки до полюса. Тогда (5.13) перепишется
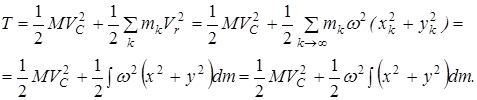
Имея в виду, что 
– момент инерции тела относительно оси z, проходящей через полюс С, последнее выражение можно переписать как
, (5.17)
при плоско – параллельном движении тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.
5. 4. Теорема об изменении кинетической энергии
5. 4. 1. Теорема об изменении кинетической энергии точки
Найдем связь между работой и изменением скорости. Пусть материальная точка массой m перемещается вдоль оси Ох под действием силы, например сжатой или разжатой пружины, закрепленной в начале координат, – точке О (рис. 5.10). Уравнение движения точки имеет вид
. (5.18)
Умножим обе части этого уравнения на 
, и, учитывая, что 
, получим
. (5.19)
В правой части этого равенства заменим Vx на 
и умножим на dt правую и левую части. Тогда
. (5.20)
В этом виде равенство имеет очень наглядный смысл: при смещении точки на dx, сила совершает работу 
, в результате чего изменяется величина кинетической энергии точки 
, характеризующая движение точки и, в частности, модуль ее скорости. Если точка смещается из положения 
в 
, а ее скорость при этом изменяется от 
до 
, то, интегрируя (5.20), имеем
. (5.21)
Учитывая, что 
, окончательно находим
. (5.22)
Изменение кинетической энергии материальной точки при ее каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.
| Рис. 5.11 |
При рассмотрении общего случая движения точки надо вместо уравнения проекций на ось (5.18) взять векторное уравнение движения
|
|
.
Проделывая все предыдущие процедуры, получим
,
здесь 
– дуга, вдоль которой перемещается точка (рис. 5.11).
5. 4. 2. Теорема об изменении кинетической энергии системы
Пусть точки системы массой 
переместились так, что их радиус-векторы 
в инерциальной системе отсчета получили приращение 
. Найдем, как при этом изменилась кинетическая энергия Т системы.
Согласно (5.11), кинетическая энергия системы
.
Вычислим дифференциал кинетической энергии системы и преобразуем полученное выражение
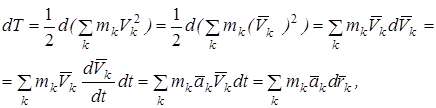
здесь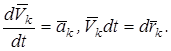 
Принимая во внимание, что 
, где 
- ускорение точки а 
и 
- равнодействующие внешних и внутренних сил, приложенных к точке, перепишем последнее равенство в виде
.
Таким образом,
. (5.23)
Последнее равенство выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме: дифференциал кинетической энергии системы равен элементарной работе всех сил системы.
Частный случай. Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:
.
Следовательно, теорему об изменении кинетической энергии (5.23) для твердого тела можно записать в виде
. (5.24)
Изменение кинетической энергии твердого тела при каком-либо элементарном перемещении равно элементарной работе внешних сил, действующих на тело.
Если обе части (5.24) проинтегрировать между двумя положениями – начальным и конечным, в которых соответственно кинетическая энергия 
и 
, получаем
. (5.25)
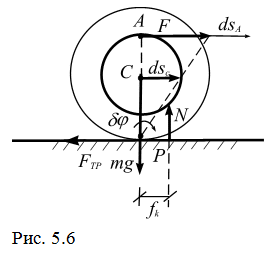
Пример 1. Диск массой m=5 кг и радиусом 
приводится в движение постоянной силой 
, приложенной в точке А (рис. 5.6). Диск катится по шероховатой поверхности вправо без скольжения. Определить скорость центра масс С катушки в момент, когда он переместится на расстояние 
, коэффициент трения скольжения 
, 
, радиус инерции диска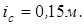 
Решение. Диск совершает плоское движение. Запишем теорему об изменении кинетической энергии для твердого тела
. (а)
Вычислим кинетическую энергию диска. В начальный момент времени диск находился в покое, т.е. 
. Кинетическая энергия в конечном положении диска
,
где 
, 
, следовательно,
.
Работа внешних сил на перемещении центра масс 
была вычислена на стр 91:
.
Находим искомую скорость центра масс диска. Имеем
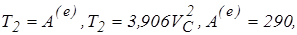
следовательно,
, откуда. VC=8,62 м/с.
Пример 2. Механическая система (рис. 5.12) состоит из составного диска 1 (m1g=40H, R1=0,4м, r1=0,2м, радиус инерции относительно оси вращения i1=0,3м), обмотанного нерастяжимыми нитями, на концах которых прикреплен груз 2 (m2g=60H) и однородный каток 3 (m3g=20H). Каток катится без скольжения по наклонной шероховатой поверхности с углом наклона 
. К диску приложена пара сил, с моментом М=80H·м, а к оси катка сила F=800H.
Вычислить ускорение, с которым будет опускаться груз 2.
Решение. Вычислим кинетическую энергию системы, равную сумме энергией всех ее тел
. (а)
Диск (тело 1) вращается вокруг центра вращения О, груз (тело 2) движется поступательно, а каток (тело 3) – плоскопараллельно, тогда кинетическая энергия каждого тела механической системы, соответственно, имеет вид
(б)
Моменты инерции диска и катка вычисляются по формулам
. (в)
Выразим линейные и угловые скорости в выражении (б) через перемещение второго груза S и его скорость 
. Направления движений тел изображены на рис. 5.12.
Имеем: 
тогда 
;
тогда 
; (г)
тогда 
.
Здесь учтено, что расстояния, пройденные точками А, В и С, связаны между собой следующим образом: 
≡ 
.
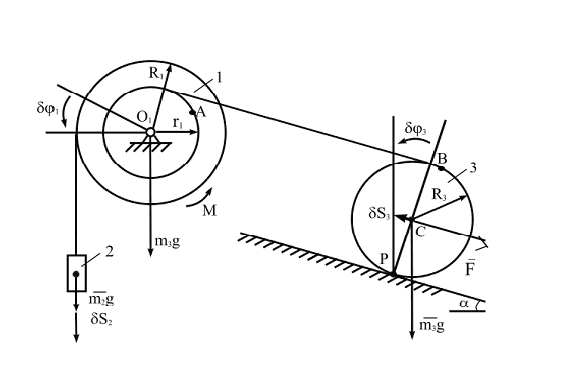
Рис. 5.12
Подставляя выражения (г) и (в) в (б), получим
;
.
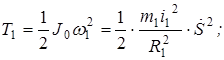
Кинетическая энергия системы равна сумме кинетических энергий элементов системы, т.е.
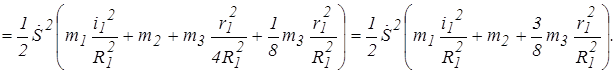
Выражение, стоящее в скобках имеет размерность массы (кг), следовательно, слагаемые в скобке представляют собой приведенную массу заданной механической системы, обозначим ее 
, тогда кинетическая энергия системы примет вид
.
Вычислим значение приведенной массы системы
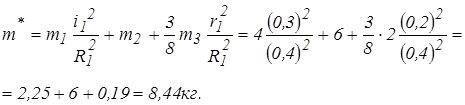
Вычислим работу, совершенную внешними силами, сообщив механической системе перемещение при котором груз 2 опустится на δS. Тогда, имея в виду (г), получим
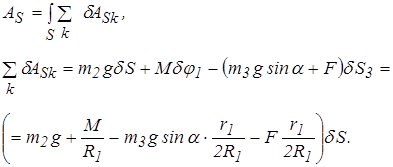
Выражение, стоящее в скобках имеет размерность силы (н), следовательно, слагаемые в скобке представляют собой приведенную силу заданной механической системы, обозначим ее 
, тогда
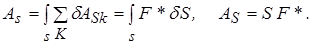
Вычислим значение приведенной силы заданной системы
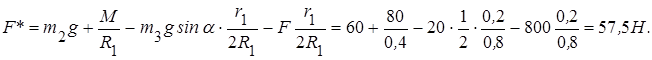
Запишем теорему (5.25)
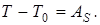
В начальный момент времени система находилась в покое, следовательно, 
Имеем
(д)
Продифференцировав по времени правую и левую части уравнения (д), получим
откуда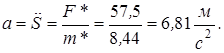 
5. 5. Закон сохранения кинетической энергии
Для механической системы имеем
, (5.26)
т.е. приращение кинетической энергии системы за конечное время равно работе всех сил системы за то же время.
Пусть все силы системы (внутренние и внешние) потенциальны, и их потенциал 
не зависит явно от времени. В этом случае элементарная работа сил системы (п. 5.2.) будет полным дифференциалом
,
тогда из (5.26) следует, что
.
Сумма кинетической и потенциальной энергии называется полной механической энергией системы. Из последнего равенства следует, что
, (5.27)
Равенство (5.27) называется интегралом движения, т.е. если все силы системы потенциальны и потенциал не зависит от времени, то при движении системы ее полная механическая энергия постоянна. Это закон сохранения механической энергии.
Следует иметь в виду, что для справедливости закона сохранения механической энергии требование о том, чтобы все силы системы были потенциальными, необязательно. Достаточно потребовать, чтобы потенциальными были силы, работа которых на действительном перемещении системы отлична от нуля.
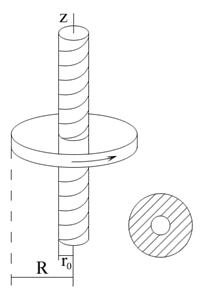
Пример. На вертикально поставленный винт надета гайка (рис. 5.13). Ей сообщена угловая скорость 
такого направления, что гайка начинает подниматься. На какую высоту поднимется гайка до остановки? Трение отсутствует.
Решение. Пусть высота подъема гайки Н, тогда работа, совершаемая весом гайки, 
. При движении гайка поднимается вдоль оси z вверх и вращается вокруг этой оси до остановки, следовательно, кинетическую энергию записать так
,
(а)
Вычислим скорость движения гайки по оси z вверх V0 и момент инерции гайки относительно этой оси Jz.
Пусть V0 скорость движения гайки вдоль оси винта в начале движения. Она найдется из пропорции
(б)
Примем, что гайка имеет форму цилиндра с осевым отверстием радиусом r. Если m масса гайки, то ее момент инерции относительно винта будет определяться следующим образом:
,
где 
- плотность.
Тогда
. (в)
Кинетическая энергия (а) с учетом (б) и (в) запишем
.
Вам также может быть полезна лекция "Эмоции и чувства".
Теорема об изменении кинетической энергии, имеем
Т1-Т0 = А,
или
,
откуда
.
