Дифракция рентгеновских лучей в кристаллах

§ 1.4.  Дифракция рентгеновских лучей в кристаллах.

Вообще говоря, дифракцией называют огибание волной препятствий, не связанное с явлениями отражения, преломления или рассеяния света. Строго говоря, дифракция является результатом интерференции вторичных волн. Основой для описания дифракции служит принцип Гюйгенса – Френеля, заключающийся в том, что все точки поверхности волнового фронта являются источниками вторичных волн, а результирующее волновое поле является суперпозицией волн, исходящих из вторичных источников. Таким образом, чтобы узнать, какова будет интенсивность в произвольной точке экрана, необходимо знать результат интерференции вторичных волн в этой точке. По идее, при дифракции на двух щелях (см. рис. 8) напротив непрозрачной части экрана должно наблюдаться тёмное пятно. Однако можно сделать так, чтобы в этой точке было пятно светлое. Это – следствие явления интерференции вторичных волн.

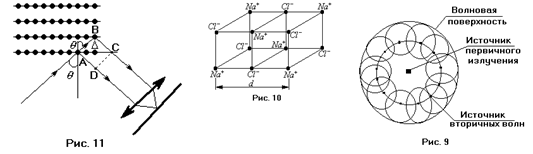
Дифракция волны на препятствии происходит всегда, независимо от размеров самого препятствия или длины волны. Другое дело, наблюдать дифракцию. Когда размеры препятствия гораздо больше длины волны, дифракцию можно обнаружить на значительном удалении от препятствия. Если же длина волны соизмерима с размерами препятствия, то дифракцию можно наблюдать в непосредственной близости от препятствия. Длина волны рентгеновского излучения составляет 1 – 0,001 нм. Поэтому, для удобства изучения рассматривают дифракцию рентгеновского излучения на кристаллах. Кристаллами называется упорядоченная структура, в узлах которой находятся молекулы, атомы, ионы или электроны. Такая структура называется кристаллической решёткой. Наиболее простой вид имеет кубическая кристаллическая решётка. Решёткой такого вида обладают графит, поваренная соль и т. д. Рассмотрим её строение на примере кристаллов поваренной соли. В узлах данной решётки сосредоточены ионы хлора и натрия. Линиями показаны химические связи, существующие в кристалле. Параметр  определяет расстояние, начиная с которого строение решётки повторяется.  называют периодом кристаллической решётки. Существуют более сложные кристаллические решётки, например, кубическая гранецентрическая кристаллическая решётка, объёмоцентрическая решётка и т. д.  Как уже говорилось ранее, существует возможность использовать кристаллическую решётку в качестве дифракционной. Однако это будет трёхмерная дифракционная решётка. Рассмотрим процессы, происходящие при прохождении луча сквозь кристалл. Если волна падает на кристалл в определённом направлении, то мы можем рассматривать процесс прохождение волны через кристалл как последовательные отражения её от кристаллических плоскостей. В этом случае ион становится источником вторичных волн. При этом часть луча отражается от ионов первой кристаллической плоскости, а другая часть проходит дальше. Так как угол падения равен углу отражения, то те фотоны, угол падения которых был одинаков, после отражения будут двигаться параллельно друг другу. Чтобы собрать их вместе, поставим на пути отражённого луча собирающую  линзу. Тогда на экране, расположенном за линзой мы сможем наблюдать дифракционную картину. Как известно, интерференционный максимум или минимум определяются тем, приходят ли волны в данную точку синфазно или же в противофазе. Разность фаз двух лучей будет зависеть от расстояния, пройденного этими лучами.

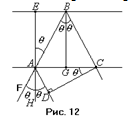
Дадим теперь явлению дифракции на кристалле некоторую количественную оценку. Отражённые лучи, как видно из рис. 11, будут иметь разность хода равную . Пусть лучи падают на кристалл под определённым углом .  Потребуем выполнения в точке наблюдения условия максимума интенсивности:  (),  где  – произвольное целое положительное число. Увеличим часть рис. 11 чтобы рассмотреть его геометрию. Очевидно, что разность хода  будет определяться следующим соотношением:  (1). Так как треугольники   и равны1, то сторона. Найдём её.  . Нам известно, что  – период кристаллической решётки. Тогда          (2). Таким образом,  (3). Рассмотрим  теперь . Угол . Этот факт легко доказывается, если записать выражения для всех углов треугольника1. Поэтому  . Таким образом,  или  . Так как , то . Возвращаясь к выражению (1), с учётом последнего выражения, а также уравнения (3), мы можем записать: . Преобразуем последнее выражение: ;  ,   (4). С другой стороны, разность фаз между волнами, отражёнными от соседних поверхностей, равна .  Так как мы требовали условие интерференционного максимума, то, в соответствии с формулой (), мы можем записать: . Учитывая выражение для  (4), получим:. По определению . Подставляя это выражение в последнюю формулу, получим:  или, окончательно,     (5). Формула (5) называется условием Вульфа – Брэгга. Она показывает, под каким углом на кристалл с заданным периодом кристаллической решётки должно падать излучение, чтобы было возможным наблюдение интерференционных максимумов.

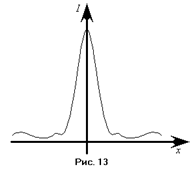
В тоже время, с помощью формулы (5) мы можем определить период кристаллической решётки исследуемого кристалла. Известно, что в случае объёмной кристаллической решётке, особенно острым будет  центральный   максимум, т. е.  (см. рис. 13). Поэтому, посылая на кристалл лучи под различными углами, мы при каком-то конкретном угле сможем наблюдать максимум. Зная угол, легко определить и период кристаллической решётки. На формуле Вульфа – Брэгга основан метод рентгеноскопического анализа. Методы рентгеноскопического анализа делятся на две группы в зависимости от условий съёмки:

Рекомендуемые материалы

1. Угол падения луча на кристалл постоянен, но изменяется длина падающей волны.

2. Длина волны постоянна, но изменяется угол падения её на кристалл.

К первому типу относится метод Лауэ. Его суть заключается в том, что на кристалл ориентированный под определённым углом по отношению к лучу, падает пучок непрерывного излучения2. Для излучения с некоторой длиной волны выполнится условие Вульфа – Брэгга. По интерференционной картине и геометрии опыта легко вычислить длину этой волны, а значит и период кристаллической решётки.

Второй тип осуществляется двумя методами.

Если Вам понравилась эта лекция, то понравится и эта - ФАЛЕС Милетский.

1. Метод вращения (метод Брэгга). Данный метод заключается в том, что монокристалл облучается монохроматическим рентгеновским излучением. При этом кристалл вращается вокруг оси кристаллографической зоны, ортогональной падающему пучку света так, что различные плоскости кристалла становятся последовательно в положение, соответствующее условию Вульфа – Брэгга. Для какого-то угла условие Вульфа – Брэгга будет выполнено. Зная угол, и результат интерференции, можно найти период кристаллической решётки. Так как излучение падает на различные кристаллические плоскости, то мы в случае сложного строения кристалла сможем полностью определить все расстояния между различными его плоскостями. Поэтому метод Брэгга используется, в основном, для анализа сложных кристаллических структур.

2. Метод Дебая – Шерера. В этом методе поликристалл или мелкий порошок из монокристаллических зёрен освещался монохроматическим излучением. Среди множества произвольно ориентированных монокристаллов всегда будут существовать такие, для которых будет выполнено условие Вульфа – Брэгга. Зная интерференционную картину, длину падающей волны и геометрию опыта, можно сделать заключение о строении кристалла.

Таким образом, опыты по дифракции рентгеновского излучения на кристалле позволили убедительно доказать волновую природу данного излучения, а также найти длину его волны.

1 , следовательно, угол . Угол , так как угол падения равен углу отражения. В свою очередь,  как внутренние, накрест лежащие. Так как углы  и  – смежные, то они равны. Поэтому . Сторона  является для треугольников   и  общей, поэтому по признаку равенства треугольников (сторона и прилегающие к ней углы равны) имеем равенство искомых треугольников.

1 . Так как сумма всех углов треугольников равна , то  или . Таким образом, . Следовательно, .

2 То есть в таком излучении представлены все длины волн.