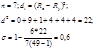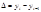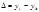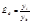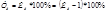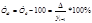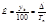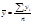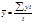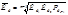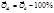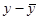Ряды динамики
Тема №
Ряды динамики
1. Понятие, уровни, виды и характеристика рядов динамиков
2. Использование рядов динамиков
3. Средняя характеристика рядов динамиков
4. Выявление и характеристика основных тенденций развития
5. Исследование сезонных колебаний
Ряды динамики – числовые значения статистического показателя, представленные во временной последовательности. Значение показателя составляющего ряды динамики называются уравнением ряда. Каждый ряд динамик характеризуется двумя показателями: значением времени и значением уровня ряда.
В качестве значения времени может использоваться день, месяц, год.
Ряды динамики можно классифицировать по следующим признаком в зависимости от временного параметра: интервальные и моментные. В интервальном ряду приводят долевые характеризующие величины за определенный период времени (сутки, месяц, квартал, год). Особенностью интервальных рядов является то, что их уровни можно суммировать. В моментном ряду приводятся данные характеристики размера явления на определенный момент времени. Суммировать уровни нельзя, т.к. последующий уровень частично содержать предыдущий.
По способу выражения уровней ряды динамики подразделяются на: абсолютные, средние и относительные величины.
Важнейшим условием формирования рядов динамиков является сопоставление уровней. Все уровни должны быть не только в одинаковых единицах измерения, также должен быть одинаковый временной параметр, т.е. прежде чем перейти к выражению рядов динамиков, нужно обеспечить сопоставление уровней рядов динамиков. Т.о., можно сказать, что прибегают к дополнительным расчетам. 
| Дата | Март | Апрель | Май | Июнь |
| Количество рабочих А | 215 | 238 | 250 | 366 |
| Количество рабочих В | 258 | 285 | 300 | 380 |
Показатели рядов динамиков:
· абсолютный прирост;
· коэффициент роста, темп роста;
· темп прироста;
· абсолютное значение чистого процента прироста.
Их можно исчислять с переменными и постоянными базами сравнения. Если производить сравнение последующего ряда с предыдущим, то получают показатели с переменно базой или ценные показатели. Если каждый последующий уровень сравнивать с начальным или каким-либо другим уровнем, принятым за базу сравнения, получают показатели с постоянной базой сравнения и их называют базисные показатели динамики.
¾ yi – уровень текущего периода;
¾ yi-1 – уровень предыдущего периода;
¾ yk – начальный уровень или уровень принятый за базу.
| Методы расчета показателей динамики | ||
| Показатель | Переменные базисы сравнения показателей | Базисный показатель |
| Абсолютный прирост |
|
|
| Коэффициент роста |
|
|
| Темп роста (%) |
|
|
| Темп прироста (%) |
|
|
| Абсолютное материальное значение признака |
|
|
| Средние характеристики ряда динамики | |
| Показатель | Метод расчета |
| Средний уровень ряда для интервального ряда |
|
| Средний уровень ряда для моментного ряда с равными интервалами |
|
| Средний уровень ряда для моментного ряда с наравными интервалами |
|
| Средний абсолютный прирост |
|
| Коэффициент роста |
|
| Темп роста |
|
| Средний темп прироста |
|
| Среднее значение признака |
|
Методы выявлении основных тенденций рядов динамиков:
1. Метод укрупнения интервалов – основан на укрупнении периодов времени, к которым относятся уровни. Например ряд недельных данных можно преобразовать в ряд месячных данных. Уровни нового ряда могут быть получены путем суммирования уровней исходного ряда, либо могут представлять средний уровень ряда.
2. Метод простой скользящей средней – основан на том, что отдельные уровни ряда динамиков сглаживаются при помощи скользящей средней. Вычисляется средний уровень из определенного числа первых по порядку уровней, а затем средний уровень из такого же числа уровней начиная со второго, далее начиная с 3-го и т.д. Т.о., при вычислении средних уровней они как бы скользят по ряду динамики
Различаются следующие зависимости: функциональная – для одного факторного признака соответствует дно и только одно значение результативно признака и стохастическая – если причинная зависимость проявляется не в каждом отдельном случае, а в общем среднем при большом числе наблюдений, частным случаем стохастической связи является корреляционная связь, при которой среднее изменение результативного признака обусловлено изменением факторных признаков. Связи между явлениями и процессами классифицируются по:
Степени тесноты связи:
| Вид связи | |
| r = До + - 0,3 | Практически отсутствует |
| + - 0,3 до + - 0,5 | Слабая |
| + - 0,5 до + - 0,7 | умеренная |
| + - 0,7 до + - 1 | Сильная |
По направлению:
· Прямая
· Обратная
По аналитическому выражению:
· Линейные связи – связь между явлениями может быть выражена уравнением прямой  .
.
· Не линейные связи – если связь выражается какой либо прямой  , либо показательной функцией
, либо показательной функцией  или гиперболой
или гиперболой  .
.
Пример: имеются следующие данные о прибыли численности рабочих на предприятии:
| № предприятия | (Y) Прибыль (млн. руб) | (X) Численность работающих |
| 1 | 119 | 210 |
| 2 | 120 | 312 |
| 3 | 123 | 356 |
| 4 | 121 | 331 |
| 5 | 122 | 347 |
| 6 | 126 | 368 |
| 7 | 128 | 385 |
| 8 | 127 | 379 |
| 9 | 131 | 392 |
| 10 | 139 | 398 |
Методом приведения параллельных данным ранжируем численность рабочих по возрастанию
| № предприятия | (X) Численность работающих | (Y) Прибыль (млн. руб) |
| 1 | 210 | 119 |
| 2 | 312 | 120 |
| 3 | 331 | 121 |
| 4 | 347 | 122 |
| 5 | 356 | 123 |
| 6 | 368 | 126 |
| 7 | 379 | 127 |
| 8 | 385 | 128 |
| 9 | 392 | 131 |
| 10 | 398 | 139 |
В статистике принято различать следующие виды зависимостей:
1. Парная корреляция – связь между двумя признаками
2. Множественная корреляция – зависимость между одним результативным признаком и несколькими факторными признаками (от 2-х и более)
3. Частная корреляция – зависимость между результативным и факторным признаками при фиксированном значении других факторных признаков
…………………………………..В котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин. При построении регрессионных моделей должны соблюдаться следующие требования:
1. Совокупность исследуемых данных должна быть однородной и математически описываться непрерывными функциями
2. Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей
3. Все факторные признаки должны иметь количественное выражение
4. Наличие достаточно большого объема исследуемой выборочной совокупности
5. Причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной форме зависимости
6. Отсутствие количественных ограничений на параметры модели связи
7. Постоянство территориальной и временной структуры изучаемой совокупности
· Парная регрессия может быть описана уравнениями записанными ранее в лекции:  ,
,  ,
,  ,
,  . Чтобы определить тип уравнения можно построить график, либо использовать неграфические способы. Если результативный и факторный признак возрастают одинаково, то это говорит о том, что связь линейная и строим уравнение прямой
. Чтобы определить тип уравнения можно построить график, либо использовать неграфические способы. Если результативный и факторный признак возрастают одинаково, то это говорит о том, что связь линейная и строим уравнение прямой , если связь обратная, то строим уравнение гиперболы
, если связь обратная, то строим уравнение гиперболы  , если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то прибегают либо к уравнению параболы или степенной функции. A0, a1,a2 – в основе которых лежит наблюдений исследуемой совокупности и нахождении параметров моделей, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, т.е. полученных на основе выбранной модели
, если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то прибегают либо к уравнению параболы или степенной функции. A0, a1,a2 – в основе которых лежит наблюдений исследуемой совокупности и нахождении параметров моделей, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, т.е. полученных на основе выбранной модели  .
.
Система нормальных уравнений для нахождения параметра линейной парной регрессии методом наименьших квадратов:

По параметру а0 можно оценить усредненное влияние на результативный признак неучтенных факторных признаков, по параметру a1 …………………… при увеличении собственного признака.
Зависимость между размером чистого дохода и объемом вложений коммерческих банков одного из регионов РФ:
| № банка | (Y) Чистый доход (млрд. дол) | (X) Объемов вложения (млн. дол.) | xiyi | Xi2 |
| 1 | 0,1 | 8,8 | 0,88 | 77,44 |
| 2 | 1,3 | 9,4 | 12,22 | 88,36 |
| 3 | 0,1 | 10,0 | 1,00 | 100,00 |
| 4 | 2,6 | 10,6 | 27,56 | 112,36 |
| 5 | 0,1 | 11,0 | 1,10 | 121,00 |
| 6 | 0,3 | 11,9 | 3,57 | 141,61 |
| 7 | 4,6 | 12,7 | 58,42 | 161,29 |
| ИТОГО: | 17,1 | 74,4 | 104,75 | 802,06 |

При увеличении объемов вложений на 1000000$ величина чистого дохода возрастает в среднем на 0,982 млрд. дол
Многофакторная (множественная регрессия):  , а0, а1, а2 – параметры уравнения, ух – результативный признак, х1, х2 - факторные признаки.
, а0, а1, а2 – параметры уравнения, ух – результативный признак, х1, х2 - факторные признаки. 
Система нормальных уравнений для нахождения наших параметров имеет следующий вид:

На основе показателей деятельности предприятий региона постройте уравнение регрессии (аналитическая форма связи)
| № предприятия | Выручка от реализации продукции (млн. руб) (Y) | Основные фонды (млн. руб) (X1) | Затраты на рекламу (%) (X2) | X12 | X22 | X1X2 | X1Y | X2Y |
| 1 | 3,0 | 6,8 | 3,5 | 46,24 | 12,25 | 23,8 | 20,4 | 10,5 |
| 2 | 5,4 | 11,2 | 6,7 | 125,44 | 44,89 | 75,04 | 60,48 | 36,18 |
| 3 | 5,9 | 9,1 | 6,8 | 82,81 | 46,24 | 61,88 | 53,69 | 40,12 |
| 4 | 4,8 | 6,9 | 5,9 | 47,61 | 34,81 | 40,71 | 33,12 | |
| 5 | 3,3 | 6,4 | 3,8 | 40,96 | 14,44 | 24,32 | 21,12 | |
| 6 | 3,4 | 6,9 | 4,3 | 47,61 | 18,49 | 29,67 | 23,46 | |
| 7 | 5,3 | 12,2 | 6,9 | 148,84 | 47,61 | 84,18 | 64,66 | |
| Итого: | 31,1 | 59,5 | 37,9 | 539,51 | 218,73 | 339,6 | 276,93 | 178,85 |

Вывод: при изменении основных фондов на 1 млн. руб. выручка изменяется (увеличивается) на 0,082 млн. руб., при изменении затрат на рекламу на 1 % выручка изменяется на 0,879 млн. руб., т.е. наблюдается прямая зависимость.
Параметрические методы изучения связи. Измерение тесноты и направления связи определяется при помощи следующих коэффициентов:
· Линейного коэффициента корреляции 
· Корреляционного отношения (эмпирического и теоретического)  эмпирическая формула рассчитывается когда характеризуется отклонение групповых средних результативного признака от общей средней.
эмпирическая формула рассчитывается когда характеризуется отклонение групповых средних результативного признака от общей средней.  - теоретическая формула
- теоретическая формула  - дисперсия альтернативного признака, рассчитанная по уравнению, регрессии,
- дисперсия альтернативного признака, рассчитанная по уравнению, регрессии,  - дисперсия результативного признака, рассчитанная по фактическим и эмпирическим данным,
- дисперсия результативного признака, рассчитанная по фактическим и эмпирическим данным,  - разность между общей и средней дисперсией
- разность между общей и средней дисперсией 
· Множественного коэффициента корреляции, вычисляется при наличии линейной связи между результативными и несколькими факторными пизнаками, а также между парой факторных признаков:

Рассчитаем, как влияет факторные признаки на результативность:
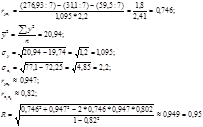
· Средний коэффициент эластичности  показывает на сколько процентов изменяется результативный признак при изменении факторного на 1 %.
показывает на сколько процентов изменяется результативный признак при изменении факторного на 1 %.
· Частных коэффициентов корреляции
Два последних коэффициента используются при многофакторной регрессии
Непараметрические методы изучения связей
Непараметрические методы определения тесноты связей. Существуеют коэффициенты ассоциации  (КА) и контингенции
(КА) и контингенции  (КК), чтобы определить эти коэффициенты строят таблицу 4-х полей с частотами:
(КК), чтобы определить эти коэффициенты строят таблицу 4-х полей с частотами:
| Показатели | A |
| Итого |
| B | A | b | A+b |
|
| c | D | D+c |
| итого | A+c | B+d | A+b+c+d |
 То связь подтверждается
То связь подтверждается
Коэффициент Пирсона  ш
ш
Коэффициент Чупрова 


К1 и К2
Коэффициенты Пирсона и Чупрова меняются от 0 до 1
Коэффициент Фехнера 
Nа – количество совпадении знаков отклонений индивидуальных величин факторного признака и результативного от их средней арифметической величины
Nb – количество не совпадений знаков отклонений индивидуальных величин факторного и результативного признака от их средней величины. Он от -1 до +1.
Ранговый коэффициент Спирмена 
Di разность между величинами рангов признака фактора и результативного признака
Ро –
Проверка адекватности регрессионной модели. Адекватность – соответствие фактическим статистическим данным наших теоретических данных. Чтобы проверить адекватность регрессионной модели нужно оценить F – критерий Фишера. 
M – число параметров модели
N – число единиц совокупности

Эмпирическое значение Фишера сравнивается с табличным с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m – 1), (n – m), если  , то уравнение регрессии признается значимым.
, то уравнение регрессии признается значимым.
После проверки модели на адекватность необходимо проверить параметры на адекватность, т.е. проверяем значимость параметров с помощью t-критерия Стьюдента. 
Эмпирическое значение Стьюдента сравнивается с табличным с уровнем значимости 0,01 или 0,05, если  , то уравнение регрессии признается значимым.(поменяй условие)
, то уравнение регрессии признается значимым.(поменяй условие)
Значимость линейного коэффициента корреляции с помощью t-критерия: 
Если  , то коэффициент корреляции признается значимым и связь подтверждается.
, то коэффициент корреляции признается значимым и связь подтверждается.
Чтобы проверить, какие показатели (признака) необходимо включать в множественную модель корреляции используют частные коэффициенты корреляции.

| Чистый доход (Y) | Объем вложений (Х) |
|
|
| 0,1 | 8,8 | - | - |
| 1,3 | 9,4 | - | - |
| 0,1 | 10,0 | - | - |
| 2,6 | 10,6 | - | + |
| 0,1 | 11,0 | + | - |
| 0,3 | 11,9 | + | - |
| 4,6 | 12,7 | + | + |
| 17,1 | 74,7 |
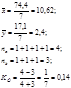
| Чистый доход (Y) | Объем вложений (Х) |
|
| Rx | Ry | di |
| 0,11 | 8,8 | - | - | 1 | 1 | 0 |
| 1,3 | 9,4 | - | - | 2 | 5 | -3 |
| 0,12 | 10,0 | - | - | 3 | 2 | 1 |
| 2,6 | 10,6 | - | + | 4 | 6 | -2 |
| 0,13 | 11,0 | + | - | 5 | 3 | 2 |
| 0,3 | 11,9 | + | - | 6 | 4 | 2 |
| 4,6 | 12,7 | + | Если Вам понравилась эта лекция, то понравится и эта - Лабораторная работа №А. + | 7 | 7 | 0 |
| 74,7 |