Направляющие системы
Раздел 16. Направляющие системы.
16.1. Прямоугольный волновод
Электрические волны ( и
и  ) тип волны Е
) тип волны Е 


 (12.3. 14) имеет в декартовой системе координат вид :
(12.3. 14) имеет в декартовой системе координат вид :  1
1
Решение (1) :  2
2
где Х(Х) - функция только Х , Y(y) - функция только Y .
(2)® (1) Þ  3
3
Рекомендуемые материалы
Выполнение (3) при произвольных значениях Х и Y возможно, если
 4
4
где  5
5
 6
6
Решение (6) имеет вид:
 7
7
(7)® (2) Þ  (*) .
(*) .
Т.к. стенки волновода предполагаются идеально проводящими , то, применяя граничное условие  :
:  при х=0 ,х=a и при y=0, y=в
при х=0 ,х=a и при y=0, y=в
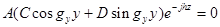
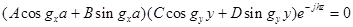
это возможно , если : ,
,
для этого необходимо :  8
8
где  и имеет смысл амплитуды продольной составляющей
и имеет смысл амплитуды продольной составляющей  .
.
(1)и (2) в декартовой системе координат имеют вид :
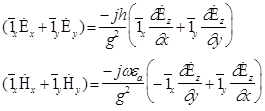
Подставляя (8) получим :
 9
9
Как следует из (8) , (9) структура поля волн типа Е в плоскости поперечного сечения соответствуют структуре стоячих волн, причем m равно числу полуволн , укладывающихся вдоль стенки длиной а , и n - число полуволн , укладывающихся вдоль стенки длиной в . Каждой паре чисел m и n соответствует определенная структура ЭМП , обозначаемая Еmnа .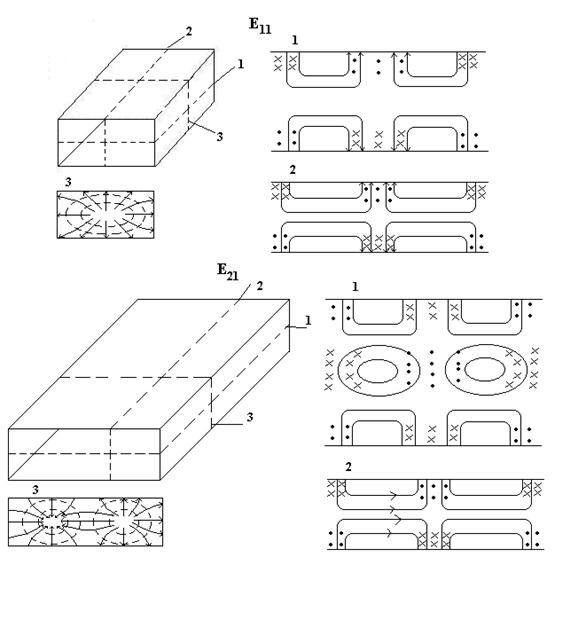
Отметим, что структуру волны Еz1 можно получить повторением структуры волны Е11 вдоль соответствующей координаты .
 ,
,
 ,
,
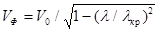
 ,
,
 .
.
Низшим типом среди волн Еmn , обладающей наибольшей lкр , является волна Е11 .Волны Еmn с различной структурой поля , которым соответствуют одинаковые значения g , имеют равные коэффициенты распространения , фазовые скорости и скорости распространения энергии , называются вырожденными .
16.2. Магнитные волны( и
и  )
)


 (12.3.15) имеет в декартовой системе координат вид :
(12.3.15) имеет в декартовой системе координат вид :  10
10
 11
11
На поверхности идеально проводящих стенок волновода должно выполнятся граничное условие :  .
.
 12
12
 13
13
Подставляя (12) , (13) в (11) , приходим к соотношениям
 14
14
Как следует из (14) , у волн Н ,как и у волн Е ,
 ,
,
т.е. волны Н и Е с равными индексами являются вырожденными .
Подставляя в (11) (14) и значения  , получим :
, получим :
 15
15
где Н0Z - =АС - амплитуда продольной составляющей магнитного поля.
Соотношения (8.7.1) , (8.7.2) в декартовой системе координат имеет вид:
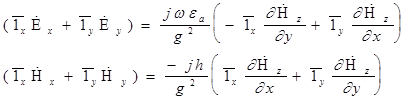
 16
16
Как следует из (15), (16) , у волн Н , как и у волн Е , структура поля в плоскости поперечного сечения соответствует структуре стоячих волн .
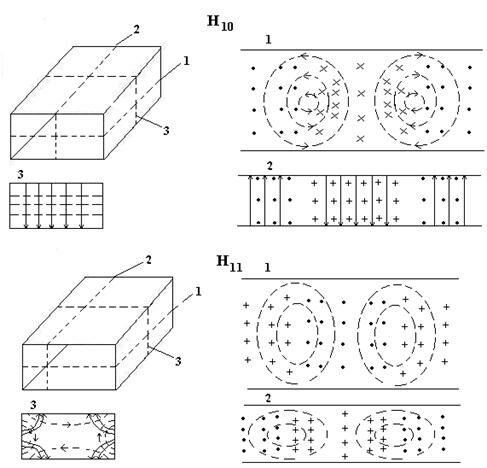
Как следует из равенств (15), (16), у волн Н, в отличие от волн Е, обращение в нуль одного из индексов ( m или n) не влечет за собой обращения в нуль всех составляющих поля . Поэтому, если полагать а>в, то низшим типом волн Н является волна Н10 .
 ,
,
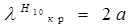
Поскольку  , то волна Н10 является низшим типом волны не только среди волн Н , но и среди всех возможных типов волн в прямоугольном волноводе . Это означает , что при l>2а передача энергии по прямоугольному волноводу невозможна .
, то волна Н10 является низшим типом волны не только среди волн Н , но и среди всех возможных типов волн в прямоугольном волноводе . Это означает , что при l>2а передача энергии по прямоугольному волноводу невозможна . 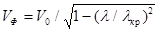 ,
,
 ,
,
 .
.
16.3. Волна Н10
Волна Н10 имеет наибольшую критическую длину волны . Поэтому на заданной частоте размеры поперечного сечения волновода . при котором возможна передача энергии по волноводу , наименьшие для этой волны .
Полагая в (15), (16) m=1 и n=0 , получим :
 17,
17,
 18
18
 19
19
 20
20
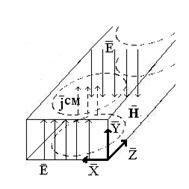
Остановимся на картине распространения поля волны Н в плоскостях параллельных широкой стенке волновода .
В ЭМП волны Н10 , магнитные силовые линии охватывают токи смещения , текущие между широкими стенками параллельно оси у .
Максимальная плотность тока смешения находится в центре замкнутых магнитных силовых линий , где напряженность электрического поля равна
нулю
 .
.
 ,
,
 ,
,
 ,
,
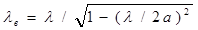
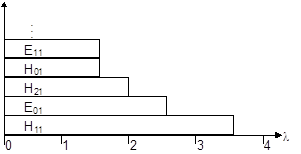
16.4. Диаграмма типов волн прямоугольного волновода
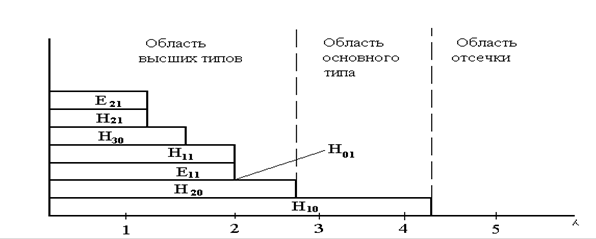
 16.5. Круглый волновод.
16.5. Круглый волновод.
В круглом волноводе возможно раздельное существование волн E и H и невозможно распространение волн T.
16.6. Электрические волны
При анализе воспользуемся цилиндрической системой координат, совместив ось с продольной осью волновода.
Ур-ние  в полярной системе координат примет вид:
в полярной системе координат примет вид:  1
1
Решение (1):  2
2
Подставив (2) в (1), умножив обе части на r2, выпполнив дифференцирование и разделив полученное уравнение на  , получим
, получим
 3
3
Левая часть (3) зависит только от r, правая - только от j. Переменные r и j - независимые. Следовательно (3) - равенство двух независимых функций. Это возможно, если каждая из функций равна постоянной. Обозначая постоянную m2, приходим к двум дифференциальным уравнениям:
 4
4
 5
5
 6
6
 7
7
Решение уравнения (4) имеет вид
 ,
,
где A и B - произвольные постоянные. Условие (7) выполняется, если m=0,1,2...
Уравнение (5) является уравнением Бесселя. Его решение можно представить в виде  9
9
где  и
и  - функции Бесселя m-го порядка первого и второго рода, а
- функции Бесселя m-го порядка первого и второго рода, а  - произвольные постоянные.
- произвольные постоянные.
 10
10
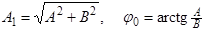
В отношении (9) функция Бесселя второго рода при  стремится к ¥. Т.к. напряженность поля в любой точке волновода должна быть ограничена, то необходимо потребовать
стремится к ¥. Т.к. напряженность поля в любой точке волновода должна быть ограничена, то необходимо потребовать  . Тогда
. Тогда
 11
11
где  - амплитуда продольной составляющей электрического поля.
- амплитуда продольной составляющей электрического поля.
Подставим (11) в (12.6. 1) и (12.6. 2), учитывая, что  :
:
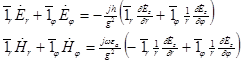
 12
12
где штрих означает дифференцирование по всему аргументу функции Бесселя.
Согласно граничному условию
 13
13
Подставляя (11) в (13), получаем
 14
14
Имеется бесконечно большое число значений аргумента, при которых функция Бесселя равна нулю. Эти значения называются корнями функции Бесселя. Обозначая n-й корень функции Бесселя m-го порядка через  , из (14) находим
, из (14) находим  , откуда
, откуда  15
15
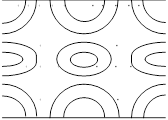
Нумерация Е волн, отличающихся друг от друга по структуре поля в плоскости поперечного сечения волновода, осуществляется в соответствии с порядковым номером корня уравнения (14). При этом индекс m соответствует числу целых стоячих волн поля, укладывающихся по окружности волновода, а индекс n характеризует распределение стоячих волн вдоль радиуса волновода.
Несколько первых корней ф-ии Бесселя  в порядке их возрастания и соответствующие им критические длины волн
в порядке их возрастания и соответствующие им критические длины волн  представлены в таблице.
представлены в таблице.
| Тип волны | E01 | E11 | E21 | E | E | E | E | E |
|
| 2.405 | 3.832 | 5.135 | 5.520 | 6.379 | 7.016 | 7.586 | 8.407 |
|
| 2.613 | 1.640 | 1.223 | 1.138 | 0.985 | 0.895 | 0.828 | 0.746 |
Низшим типом среди волн E в круглом волноводе является волна E01.
 ,
,
 ,
,
 ,
,
 ,
,


 |
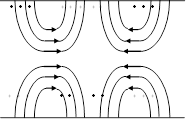
16.7. Магнитные волны ( )
)
Будем рассуждать аналогично случаю с электрическими волнами
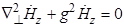
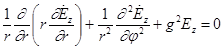
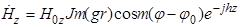
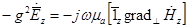
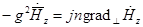
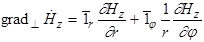
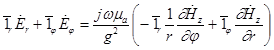
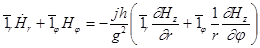
 17
17
Отметим, что при выполнении Jm(ga)=0 согласно 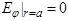
 18
18
Несколько первых корней функции Бесселя  в порядке их возрастания и соответствующие длины волн
в порядке их возрастания и соответствующие длины волн  представлены в таблице.
представлены в таблице.
| Тип волны | H11 | H21 | H01 | H31 | H41 | H12 | H51 | H21 | H02 |
|
| 1.84 | 3.05 | 3.83 | 4.20 | 5.32 | 5.33 | 6.42 | 6.71 | 7.02 |
|
| 3.41 | 2.06 | 1.64 | 1.50 | 1.182 | 1.178 | 0.979 | 0.934 | 0.838 |
Низшим типом среди не только волн H, но и всех волн в круглом волноводе, как следует из сравнения двух таблиц, является волна H11.
 19
19
Поэтому уравнение  эквивалентно уравнению
эквивалентно уравнению
 20
20
При m=0 уравнение (20) примет вид
 21
21
Из сравнения (21) и (14) вытекает, что
 22
22
т.е.  , и в круглом волноводе волны E1n и H0n являются
, и в круглом волноводе волны E1n и H0n являются
вырожденными.
 | |||||
 | |||||
 | |||||
16.8. Токи на стенках прямоугольного и круглого волноводов.
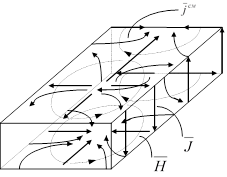
Токи в прямоугольном волноводе при распространении волны H10
 Предположим, что стенки волновода являются идеально проводящими. В этом случае токи проводимости текут по поверхности стенок. Плотность поверхностного тока численно равна напряженности тангенсальной составляющей магнитного поля у поверхности проводника. Вектор плотности поверхностного тока направлен нормально к вектору напряженности магнитного поля.
Предположим, что стенки волновода являются идеально проводящими. В этом случае токи проводимости текут по поверхности стенок. Плотность поверхностного тока численно равна напряженности тангенсальной составляющей магнитного поля у поверхности проводника. Вектор плотности поверхностного тока направлен нормально к вектору напряженности магнитного поля.  1
1
Структура поля волны H10 изображена на рис. стр. 52. Согласно (1) и (19) плотность продольного тока на широкой стенке равна
 2
2
Распределение  показано на рис. Продольные токи на нижней и верхней стенках противофазны.
показано на рис. Продольные токи на нижней и верхней стенках противофазны.
Согласно (1) и ( 17) плотность поперечного поверхностного тока на широких стенках
 3
3
Распределение  показано на рис. На узких стенках, параллельно оси y, поверхностный ток определяется только составляющей
показано на рис. На узких стенках, параллельно оси y, поверхностный ток определяется только составляющей  магнитного поля и, соответственно, имеет только составляющую
магнитного поля и, соответственно, имеет только составляющую  .
.
 |
Как следует из (17), Hz у узких стенок имеет постоянную амплитуду H0z.
Плотность поверхностного тока на узких стенках равна
 4
4
Модуль комплексной плотности тока в любой точке поверхности широких стенок волновода
 5
5
Распределение суммарной плотности тока показано на рис.
16.9. Токи в круглом волноводе при распространении волны H11
Рекомендация для Вас - 7.3 Структурно-функциональная теория культур А.Рэдклифф-Брауна.
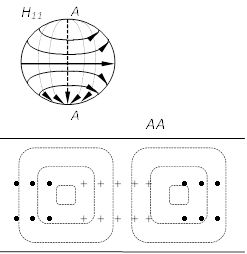
Структура ЭМП волны H11 изображена на рис. стр. 56.
 У поверхности волновода имеются две отличные от нуля составляющие вектора напряженности магнитного поля Hj и Hz, которым, согласно (1) (где следует положить
У поверхности волновода имеются две отличные от нуля составляющие вектора напряженности магнитного поля Hj и Hz, которым, согласно (1) (где следует положить  ) соответствуют составляющие тока проводимости
) соответствуют составляющие тока проводимости  .
.
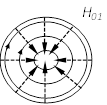
16.10. Токи в круглом волноводе при распространении волны H01
 Структура волны H01 изображена на рис. стр. 56. У поверхности волновода отлична от нуля лишь продольная составляющая магнитного поля, которая согласно ( .2. 16) по всему периметру волновода равна
Структура волны H01 изображена на рис. стр. 56. У поверхности волновода отлична от нуля лишь продольная составляющая магнитного поля, которая согласно ( .2. 16) по всему периметру волновода равна
 6
6
В соответствии с (9.3.1) на стенках волновода существуют только поперечные  поверхностные токи (кольцевые токи). Плотность этих токов одинакова по всему периметру волновода и описывается выражением (6)
поверхностные токи (кольцевые токи). Плотность этих токов одинакова по всему периметру волновода и описывается выражением (6)