Магнитные волны

Раздел 15.    Магнитные волны

(и )   15.1. Связь между составляющими поля.

Полагая в соотношениях:

   ,              

, получаем :                                       1

                               2

                                           3

                      4

Рекомендуемые материалы

Следовательно, у волн Н векторы и    взаимно перпендикулярны.

Из равенства (2) вытекает граничное условие, которому удовлетворяет составляющая  на металлических поверхностях:

         5

15.2. Характеристическое сопротивление . Фазовая скорость

Согласно (3) и (12.4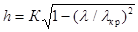.6)

         6

- чисто мнимая величина, и перенос энергии по ЛП отсутствует :,следовательно, волны Н - диспергирующие.

                     15.3. Групповая скорость

Реальные электромагнитные сигналы немонохроматическими, т. к. состоят из конечного, либо бесконечного числа монохроматических колебаний с различными частотами. В диспергирующих системах фазовая скорость зависит от частоты, т. е. проходя один и тот же путь монохроматические волны получают различные по величине фазовые сдвиги.

Для характеристики перемещения немонохроматических сигналов вводят понятие групповой скорости, понимая под этим скорость перемещения огибающей группы монохроматических волн , близких по частоте .

                  1,

где  - амплитуда каждой из монохроматических волн; b(w)- коэффициент распространения каждой их этих волн.

Если спектр сигнала достаточно узкий и заключен в интервале частот : , то =0 вне этого интервала. Поэтому ,      2.

Разложим  в ряд Тейлора

    3

где b0 - коэффициент распространения на частоте w0 . Т.к. спектр узок , то :

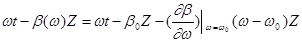
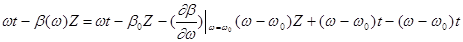
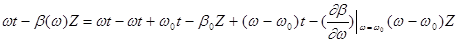
             4

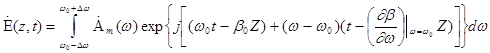
          5

Для простоты предположим, что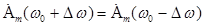

   6

Амплитуда сигнала / величина в фигурных скобках / достигает максимума , если  ,     т.е. , когда .

Скорость перемещения максимума равна :                   7

По определению эта величина - групповая скорость.

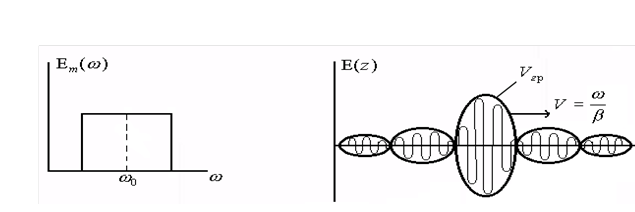
Условием применимости (7) является малая скорость изменения  вблизи w0  узость спектра сигнала. При невыполнении этих условий влияние дисперсии становится весьма значительным, и сигнал в процессе распространения так сильно меняет свою форму, что само понятие групповой скорости теряет смысл.

Получим выражение для  в ЛП:

 ,         

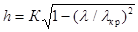
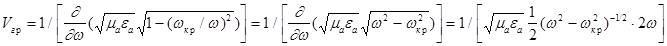
                     8

Т.е. <  для распространения волн  Е, Н  и = для волн Т.

Сравнивая (8) и (12.6.  5)    () , замечаем, что

                     9

            10

Основная энергия волны сосредоточенавблизи максимума огибающей. Поэтому, говоря о , можно читать , что мы говорим о .

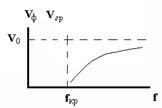
Т.о. <  для волн  Е, Н  и = для волн Т .

15.4. Мощность, переносимая электромагнитной волной по линии передачи

Средняя мощность , проходящая за период через элементарную площадку  ds :

                                       1

где  - продольная составляющая П.

            2

Из равенств        ,          ,         

следует, что для волн  Е, Н,Т  форма связи имеет одинаковый вид :                                   3

В лекции "49. Принципы и методы формирования организационной культуры" также много полезной информации.

Подставляя (3) в (2) , и учитывая, что продольные составляющие сдвинуты по фазе относительно поперечных на 90° . , получаем:

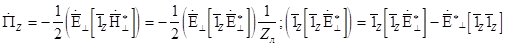
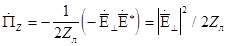
                              4

                               5

                                  6