Первое начало термодинамики с точки зрения статистической физики. Статистическое определение энтропии

1.4. Первое начало термодинамики с точки зрения статистической физики. Статистическое определение энтропии

Первое начало термодинамики для бесконечно малых величин может быть записано в виде:

.

Внутренняя энергия:  т.е. это среднее значение микроскопической внутренней энергии

           (*),

где  – дифференциал по а и Т.

Введем микроскопические (зависит от Х) силы, соответствующие обобщенным координатам :

.

Отметим, что размерность этих сил может быть различной в зависимости от параметров .

Рекомендуемые материалы

Термодинамические силы  определяются как средние от микроскопических сил: .

Работа в термодинамике может быть определена как:

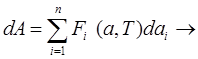
первый член (*) равен работе термодинамических сил

                           (**).

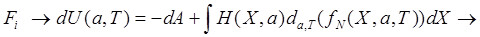
Вполне понятно, что работа связана с изменением внешних параметров, поскольку они не дают вклада в кинетическую энергию, то должны дать вклад в потенциальную.

То есть определяется изменением функции распределения вследствие изменения термодинамических переменных а, Т.

Из условия нормировки:

.                                                                          (***)

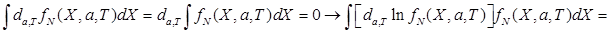
В выражении (**) разделим и умножим на  и вычтем выражение

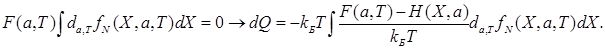
Используем каноническое распределение Гиббса:

 с учетом  – вынесем за интеграл →(***).

.

Из определения энтропии в термодинамике: .

Если приравнять величину  в каноническом распределении Гиббса к термодинамической температуре, то, сравнивая , получим:

,

где  – константа, которая может быть определена только в квантовой статистической теории. Или: .

Из термодинамики свободная энергия определяется как:

.

Таким образом, действительно функция  в каноническом распределении Гиббса совпадает со свободной энергией, определенной в термодинамике. Зная сводную энергию, можно вычислить основные термодинамические параметры:

.

Люди также интересуются этой лекцией: 2 Становление конфликтологии как науки.

Отсюда:

, .

С другой стороны можно определить теплоемкость:

.

Таким образом, основной алгоритм, на котором основана равновесная СФ, выглядит так:

.