Экстраполированный итерационный метод

3.2. Экстраполированный итерационный метод

Для симметризуемого метода (3.10)  экстраполированный метод имеет вид

                                         .                          (3.11)

Его можно переписать в виде

                                                                (3.12)

Здесь  ‑ параметр экстраполяции. Выясним сходимость экстраполированного метода (3.12). Для этого надо оценить спектр . Очевидно, собственные числа оператора перехода  равны

                               ,

а экстремумы достигаются на границах, т.е. при , либо при . Для спектра построим график функции

     (3.13)

Рекомендуемые материалы

и найдем ее минимум по . Соответствующее значение  будет оптимальным параметром экстраполяции в смысле минимизации спектра оператора перехода: . График функции (3.13) при ,  от аргумента  показан на рис. 3.1 красным цветом. При построении, графика учтено, что

                                             

а угловые коэффициенты (наклон ветвей графика) функции  болше, чем .

Рис. 3.1. К определению оптимального пaрaметра экстраполяции

Оптимальное значение  параметра экстраполяции в смысле минимизации оператора перехода итерационного метода (3.12)  находим из уравнения

                                               (3.14)

При этом значении имеем

               

Следовательно, оптимальный экстраполированный метод (RF-OE – Ричардсона с фиксированным параметром оптимально экстраполированный)

                                 

сходится, если сходится метод RF.

Перепишем итерационный процесс  в каноническом виде. Имеем

         

Применив к этому равенству оператор  и поделив на , получим

                                              .                               (3.15)

При фиксированных (не зависящих от шага )  и  метод (3.15) называют методом простой итерации. Если, кроме того, , то он становится явным, а оптимальный параметр (3.14) вычисляется по формуле

                

Итак, чтобы вычислить параметр экстраполяции (оптимальный шаг в методе простой итерации), необходимо знать границы спектра – собственные числа . Это самостоятельная, вообще очень трудная задача. Точно она решается лишь в простейших случаях. Тем не менее, нам нужны хотя бы оценки.

Собственные числа и собственные функции
простейших операторов и матриц

Рассмотрим одномерную задачу теплопроводности

                                      .                            (1)

Оценим с.ч. и с.ф. положительно определенного оператора . Для этого решим задачу Штурма-Лиувилля , или

                                              .                                    (2)

Прежде всго, для удобства сведем задачу к области  заменой . Получим , или, обозначив ,

                                                                                   (3)

Решение задачи (2) ищем в виде ряда

                                          .                               (4)

Очевидно, чтобы уловлетворить краевому условию при , следует положить . Очевидно, что решение задачи (3) определено с точностью до множителя, поэтому, не нарушая общности, можно положить  (эквивалентно делению на множитель ).

Подставим (4) в (3):

    

Очевидно, все коэффициенты при одиинаковых степенях  должны быть равны нулю. Отсюда следует рекуррентная формула для коэффициентов

                                                    (5)

Получим их явный вид:

                              

Итак, все четные равны нулю, а нечетные равны

                           

Подставим эти значения в ряд (4). Будем иметь

                               (6)

Это очень похоже на разложение в ряд Тейлора функции  в окрестности нуля:

          

Таким образом, получили решение (6) задачи (3) в виде

                                                                                          (7)

Оно удовлетворяет граничному условию , если , откуда находим собственные числа одномерного опрератора Лапласа с нулевыми граничными условиями на единичном отрезке . Вспомним, что для перехода к отрезку  достаточно сделать замену .

Окончательно получим из (7) собственные функции и собственные значения

                      .            (8)

Границы спектра таковы:

              .

Как уже отмечалось, в задаче (2) собственные функции определяются с точностью до множителя. Выберем этот множитель так, чтобы система функций вида (8) была ортонормальной, т.е. положим

                                                                                              (9)

и потребуем, чтобы

                                               .

При  имеем

          

откуда находим нормирующий множитель . Ортогональность функций (9) очевидна. Итак, имеем

                                                (10)

Главное свойство ортонормального базиса.

Любая достаточно гладкая функция , удовлетворяющая однородным краевым условиям  однозначно представима в виде ряда по ортонормальному базису (10):

                                    .                       (11)

Перейдем теперь к разностной схеме для задачи Штурма-Лиувилля (2) на равномерной сетке:

                                         (12)

Решение этой задачи определит собственные значения и соответствующие им собственные функции разностного оператора Лапласа с граничными условиями Дирихле. Базисные функции, по аналогии с дифференциальным случаем, будем искать в виде

                                   ,                       (13)

где  - произвольный множитель, а  выбрано так, чтобы удовлетворить граничным условиям. Из (12) получаем

                          

Но , поэтому имеем уравнение для

                                      

Находим (т.к. )

                .    (14)

Нетрудно видеть, что все , причем

     

При  имеем оценку границ спектра разностного оператора Лапласа

                   .      (15)

Множитель  собственных функций определим из условия их ортонормальности в смысле скалярного произведения

                                        .

При , с учетом нулевых граничных условий, подстановка (13) дает

                    

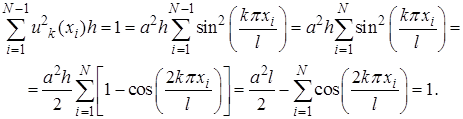
Последняя сумма равна нулю (?), поэтому имеем , и ортнормированная система собственных функций (13) принимает вид

                          (16)

Основные свойства с.ф. (16) и с.з. (14) задачи Дирихле.

1. Ортонормированность

                                                        

2. Любая сеточная функция , равная нулю на границе, , во внутренних узлах  может быть разложена в ряд по с.ф.

                                   

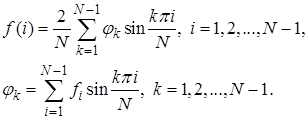
3. Ограниченность спектра с.з.

                   

Можно показать, что для расностной задачи Неймана

                   

с.з. те же, но их уже :

                     

С.ф. - косинусы

               

Эти с.ф. также образуют ортонормальный базис.

В задаче Неймана имеется нулевое с.з. , ему соответствует постоянная с.ф. , что отражает вырожденность этой задачи, т.е. ее решение определено с точностью до постоянной.

Двухслойный итерационный процесс и метод установления

Двухслойный итерационный процесс (3.15) можно трактовать как неявную (при ) схему для нестационарного уравнения

                                                        ,

а параметр  - как шаг по фиктивному времени. Различие между итерационными методами и схемами для нестационарных задач заключается в следующем:

1. При любых  и  точное решение  исходной задачи  удовлетворяет (3.15), т.е. обращает его в тождество. Для нестационарных задач это может удовлетворяться лишь при .

2. Выбор оператора (матрицы)  и параметра экстраполяции следует подчинить лишь требованиям сходимости итераций и минимума арифметических действий, необходимых для нахождения решения исходной задачи с требуемой точностью. Для нестационарных задач выбор шага подчинен прежде всего требованиям аппроксимации и устойчивости.

Выше предполагалось, что оператор  линеен (коэффициенты матрицы не зависят от решения ), однако итерационная схема (3.15) может использоваться и для нелинейных операторов, в этом случае коэффициенты матрицы  вычисляются на векторе .

Достаточное условие сходимости двухслойного итерационного процесса.

Теорема. Итерационный процесс

                                                                              (3.15)

сходится, если

                                      

Доказательство.   Пусть  - погрешность приближенного решения на -м шаге ( - точное решение задачи). Подставив это в (3.15), получим однородное уравнение для погрешности

                                               .                                     (1)

Для краткости обозначим . Уравнение (1) перепишем в виде

             

Требуется доказать сходимость, если

Если Вам понравилась эта лекция, то понравится и эта - Исследования генетики поведения собак.

                                                      

Умножим это равенство скалярно на . Будем иметь

                                .                      (2)

Но  В силу симметричности оператора  (условие 1) , поэтому второй член в (2) равен . Подставив это в (2) и воспользовавшись тем, что  (условие 2), получим

                                    

т.е. последовательность норм погрешностей убывает до нуля с ростом числа итераций , т.е. процесс сходится.