Метод Якоби (диагональный)

3.3. Метод Якоби (диагональный)

Представим матрицу  в виде суммы диагонали , нижней треугольной  и верхней треугольной : 

                                                      ,                                       (3.16)

где

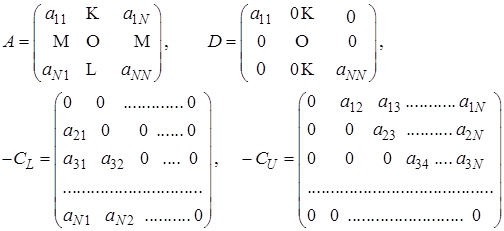
Итерационный метод Якоби в индексах выглядит так:

                                     .                      (3.17)

В матричной форме (3.17) запишется так

                                             ,

Рекомендуемые материалы

или

                              (3.18)

Если , то и , а метод Якоби (3.18) с матрицей перехода  будет симметризуемым с матрицей симметризации . Напомним, что требование симметризации в нашем случае означает, что  

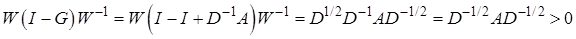
Он сходится тогда и только тогда, когда . Это условие выполняется, если матрица  имеет слабое диагональное преобладание, т.е.

                                                         .                                         (3.19)

В самом деле,

                        .

Это значит, что -я сторока матрицы  имеет вид

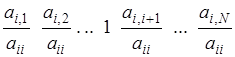
Из условия слабого диагонального преобладания (3.19) следует, что , а значит . Поскольку , то сходимость доказана.

Для метода Якоби можно применять эстраполяцию (3.11), однако для ряда типичных задач матрица  такова, что , и оптимальное значение параметра экстраполяции (3.14) равно , так что экстраполяция не нужна.

Реализация метода Jacobi.

Если матрица  заполнена, то решение задачи (3.17) выглядит так:

    (3.19)

11 Искусство Ближнего и Среднего Востока - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Однако в сеточных схемах матрица  разрежена, т.е. в каждой строке только несколько ненулевых элементов . Применение алгоритма в части вычисления  в этом случае очень неэкономично: при суммировании подавляющее большинство операций производится с нулями. Выход состоит в том, чтобы изменить формат хранения матрицы коэффициентов и по-новому определить операцию умножения матрицы на вектор. Например, диагональная схема хранения трехдиагональной матрицы РС для одномерного уравнения теплопроводности

          ,

или

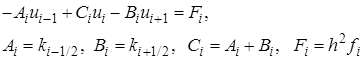
Вычисление нового приближения в программе при этом можно записать просто: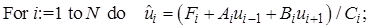 

Задание.  Составить программу решения задачи Дирихле для стационарного уравнения теплопроводности с переменными коэффициентами методом Якоби, придумать тест и численно исследовать сходимость. Сравнить с решением по методу прогонки.