Метод Гаусса-Зейделя (треугольный)
3.4. Метод Гаусса-Зейделя (треугольный)
Представим матрицу  в виде суммы диагонали
в виде суммы диагонали  , нижней треугольной
, нижней треугольной  и верхней треугольной
и верхней треугольной  :
:
 , (3.16)
, (3.16)
где
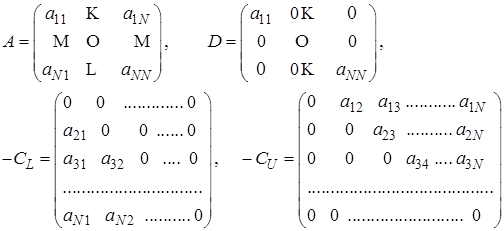
Итерационный метод Гаусса-Зейделя в индексах выглядит так:
 . (3.20)
. (3.20)
Несмотря на то, что в правую часть (3.20) входят значения на новой итерации  , вся правая часть вычисляется явно, т.к. вычисления проводятся последовательно для узлов
, вся правая часть вычисляется явно, т.к. вычисления проводятся последовательно для узлов  , и к моменту вычисления
, и к моменту вычисления  все
все  уже известны.
уже известны.
В матричной форме (3.20) имеет вид
Рекомендуемые материалы
 , (Z)
, (Z)
или
 (3.21)
(3.21)
Матрица  - матрица перехода (шага) метода Зейделя, а матрица
- матрица перехода (шага) метода Зейделя, а матрица  - матрица расщепления, которая треугольная, и разумеется не симметричная и, вообще говоря, не положительно определенная, а сам метод не симметризуем. Тем не менее, если
- матрица расщепления, которая треугольная, и разумеется не симметричная и, вообще говоря, не положительно определенная, а сам метод не симметризуем. Тем не менее, если  , то метод Гаусса-Зейделя сходится. Скорость сходимости чуть больше, чем у метода Якоби. Чтобы убедиться в сходимости метода, достаточно записать (Z) в каноническом виде и проверить условие Теоремы
, то метод Гаусса-Зейделя сходится. Скорость сходимости чуть больше, чем у метода Якоби. Чтобы убедиться в сходимости метода, достаточно записать (Z) в каноническом виде и проверить условие Теоремы  . Перепишем (Z) в виде
. Перепишем (Z) в виде
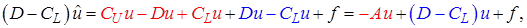
откуда получаем каноническую форму
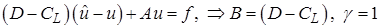
"5.3 Вопросы для самоконтроля и резюме" - тут тоже много полезного для Вас.
Итак, надо проверить условие  . Но
. Но  , а в силу условия
, а в силу условия  имеем
имеем  , поэтому
, поэтому  . Таким образом, осталось проверить
. Таким образом, осталось проверить  , или
, или  , что равносильно
, что равносильно  . Но это так, если
. Но это так, если  . Т.е. достаточное условие сходимости выполнено.
. Т.е. достаточное условие сходимости выполнено.
Важно подчеркнуть, что порядок вычислений в методе Зейделя напрямую зависит от способа нумерации узлов сетки. Поскольку вновь подсчитанные узловые значения функции немедленно подставляются на место предыдущих, можно экспериментировать с направлением обхода узлов. Например, разные направления обхода можно задать с помощью вектора перестановок индексов  , где
, где  - исходный номер, а
- исходный номер, а  - новый. Разумеется, функция
- новый. Разумеется, функция  должна быть взаимно однозначной. Пусть
должна быть взаимно однозначной. Пусть  естественное упорядочение узлов сетки по возрастанию, тогда
естественное упорядочение узлов сетки по возрастанию, тогда  задает обратный порядок. Для произвольного порядка обхода узлов следует просто заменить в формуле (3.20)
задает обратный порядок. Для произвольного порядка обхода узлов следует просто заменить в формуле (3.20)  на
на  . Особенно такой подход удобен для многомерных задач.
. Особенно такой подход удобен для многомерных задач.
При ленточной схеме хранения или при хранении матрицы в разреженном строчном формате удобен следующий прием вычислений в методе Гаусса-Зейделя. Для каждого  определятся текущий вектор неизвестных
определятся текущий вектор неизвестных  . Тогда формула (3.20) может быть переписана в виде
. Тогда формула (3.20) может быть переписана в виде
 (3.22)
(3.22)
Здесь  - это скалярное произведение
- это скалярное произведение  -й строки матрицы
-й строки матрицы  на вектор
на вектор  .
.
Задание. Составить программу решения задачи Дирихле для стационарного уравнения теплопроводности с переменными коэффициентами методом Гаусса-Зейделя, численно исследовать сходимость. Сравнить с решением по методу Якоби.























